Тренировочные задания по теме 6.1

1. Номер серии выигрышных билетов лотереи состоит из пяти цифр. Определить вероятность того, что номер первой выигравшей серии будет состоять из одних нечетных цифр.

Ответ. Р(А) = 0,03125.

2. В партии из 100 деталей имеется 10 бракованных. Для проверки отобрали 5 деталей. Какова вероятность того, что среди отобранных деталей только одна окажется бракованной?

Ответ. Р(А) = 0,0103.

5. В группе 20 студентов: 12 девушек и 8 юношей. Разыгрывается 5 путевок для отдыха. Какова вероятность того, что путевки получат 3 девушки и 2 юноши?

Ответ. Р(А) ≈ 0,17.

4. Из урны, в которой находятся 8 белых и 12 черных шаров, извлекают один шар и возвращают его обратно. Затем извлекают еще один шар. Найти вероятность того, что извлеченные два шара будут черные.

Ответ. Р(А) ≈ 0,36.

5. Меняется условие предыдущей задачи: вынимаются два шара подряд, т.е. после извлечения первого шара он в урну не возвращается. Найти вероятность того, что извлеченные два шара будут черные.

Ответ. Р(А) ≈ 0,347.

6. Имеется три одинаковых на вид урны: в первой урне два белых и один черный шар; во второй – три белых и один черный; в третьей – два белых и два черных шара. Наугад выбирается урна и из нее вынимается шар. Найти вероятность того, что этот шар белый.

(Используем формулу полной вероятности).

Ответ. Р(А) = 23/36.

7. Два стрелка независимо друг от друга стреляют по одной мишени, делая каждый по одному выстрелу. Вероятность попадания в мишень у первого стрелка 0,8 , а у второго – 0,4. После стрельбы в мишени обнаружена одна пробоина. Найти вероятность того, что мишень поражена первым стрелком.

(Используем формулу Байеса).

Ответ. Р(А) = 6/7.

8. Вероятность попадания в цель при отдельном выстреле составляет р=0,8. Найти вероятность пяти попаданий при 6 выстрелах.

Ответ. 0,3932.

9. Всхожесть семян данного сорта растения оценивается вероятность. 0,8. Какова вероятность, что из 5 посеянных семян взойдет не меньше четырех?

Ответ. 0,73728.

10. Вероятность выхода прибора из строя р=0,005. Найти вероятность того, что из 1000 приборов три выйдут из строя.

Ответ. ≈ 0,146.

11. Бросаются три игральные кубика. Определить вероятность появления ровно 8 очков.

Ответ. 0, 097.

Контрольные вопросы по теме 6.1

1. Случайные события и их классификация.

2. Классическая формула теории вероятности.

3. Статистическое определение вероятности.

4. Теорема сложения вероятностей.

5. Теорема умножения вероятностей.

6. Формула полной вероятности.

7. Формула Байеса.

Литература. А: 2—4, 7, 8, 9, 11; Б: 8, 9.

2. Случайные величины

Случайной называется величина, которая в результате опыта может принять различные заранее неизвестные значения. Различают два вида случайных величин – дискретные и непрерывные.

Дискретной случайной величиной называется такая величина, которая может принимать любое значение из конечного или бесконечного счетного множества значений, т.е. такое множество, элементы которого могут быть занумерованы и выписаны в последовательности …

Непрерывной случайной величиной называется такая величина, которая может принимать любые неизвестные заранее значения из рассматриваемого участка или интервала.

Законом распределения (или рядом распределения) дискретной случайной величины называется соответствие между ее значениями и их вероятностями.

Закон распределения может задаваться таблицей, формулой или графиком. При табличном задании первая строка содержит возможные значения, вторая – вероятности этих значений

Х			……..
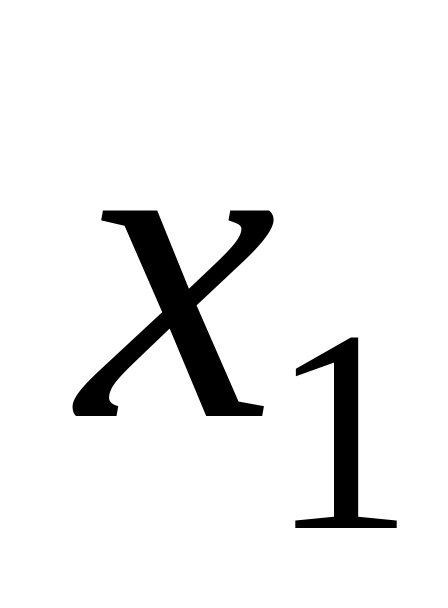
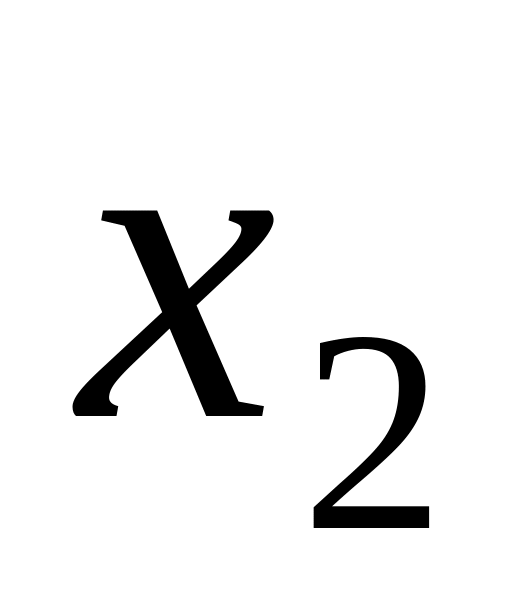
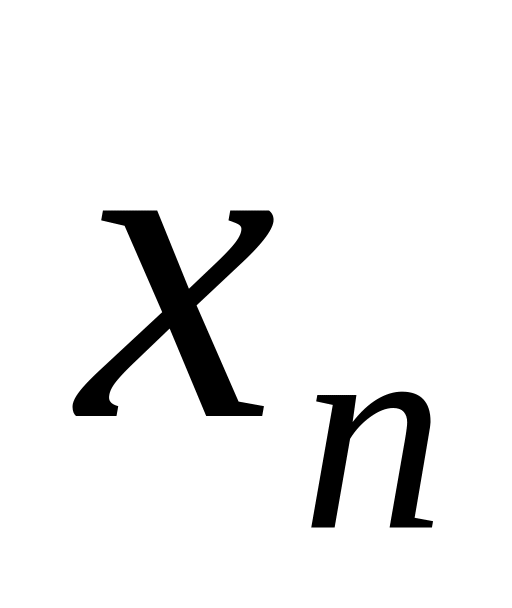
р			……..

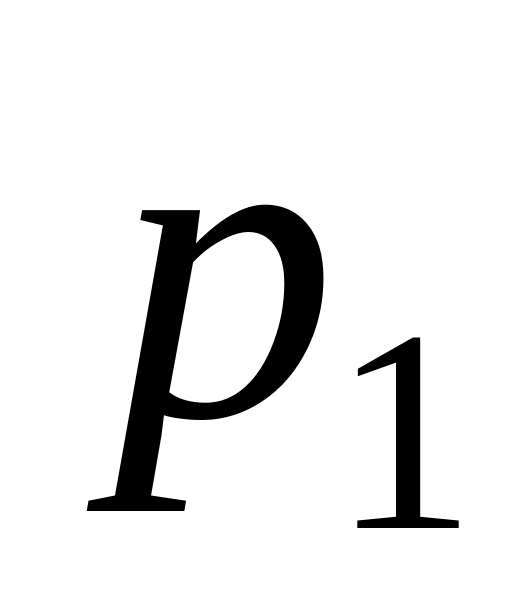
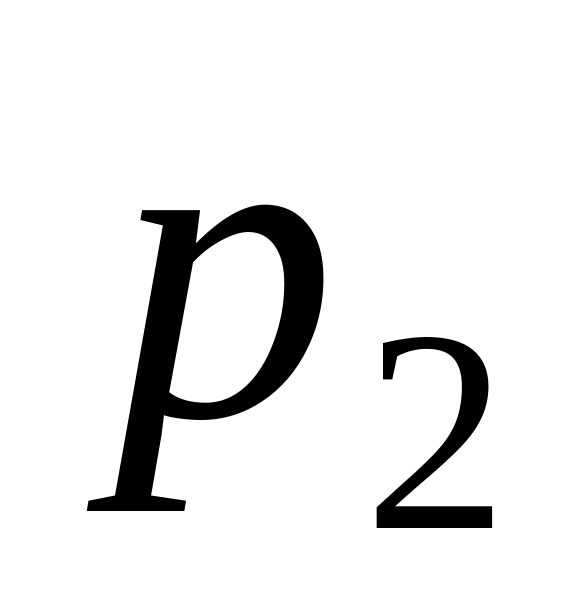
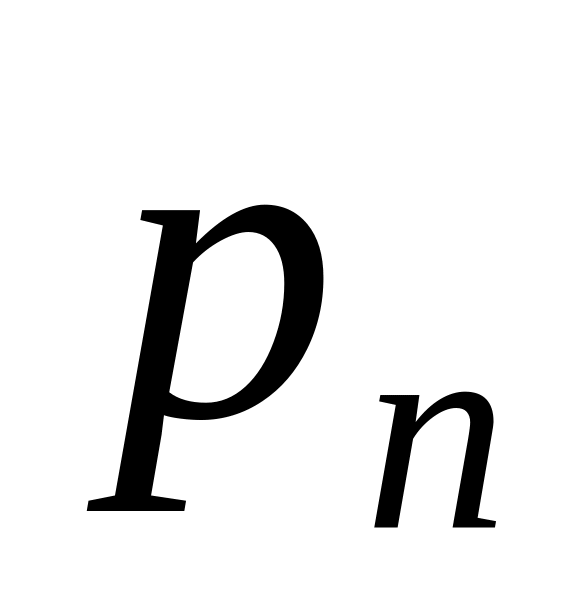
В любом законе распределения необходимо перечислять все возможные значения случайной величины, следовательно события образуют полную группу событий и + +..+ =1.

Функция распределения вероятностей случайной величины

Дискретная случайная величина может быть задана перечнем всех её возможных значений и их вероятностей. Такой способ задания неприемлем для непрерывной случайной величины.

Действительно, рассмотрим случайную величину Х, возможные значения которой сплошь заполняют интервал . Очевидно, что перечень всех значений Х составить невозможно. Этот пример указывает на целесообразность дать общий способ задания любых типов случайных величин. С этой целью вводят функцию распределения случайной величины.

Пусть х – действительное число. Вероятность события, состоящего в том, что Х примет значение, меньшее х, т.е. вероятность события , обозначим через F(х). Очевидно, что если х изменяется, то меняется и F(х), т.е. F(х) – функция от х.

Функцией распределения случайной величины Х называют функцию F(х), определяющую вероятность того, что случайная величина Х в результате испытания примет значение, меньшее х, т.е.

Геометрически это равенство можно истолковать так: F(х) есть вероятность того, что случайная величина примет значение, которое изображено на числовой оси точкой, ледащей левее точки х.

Иногда вместо термина «функция распределения» используется термин «интегральная функция».

Свойства функции распределения:

- значения функции распределения принадлежат отрезку [0, 1]: ;

- F(х) – неубывающая функция, т.е. , 6если ;

- вероятность того, что случайная величина примет значение, заключенное в интервале , равна приращению функции распределения на этом интервале: ;

- вероятность того, что непрерывная случайная величина Х примет одно определенное значение, равна нулю;

- если возможные значения случайной величины принадлежат интервалу , то: при и при ;

- если возможные значения непрерывной случайной величины расположены на оси х, то справедливы следующие предельные соотношения: ; .

Изложенные выше свойства позволяют представить, как выглядит график функции распределения непрерывной случайной величины.

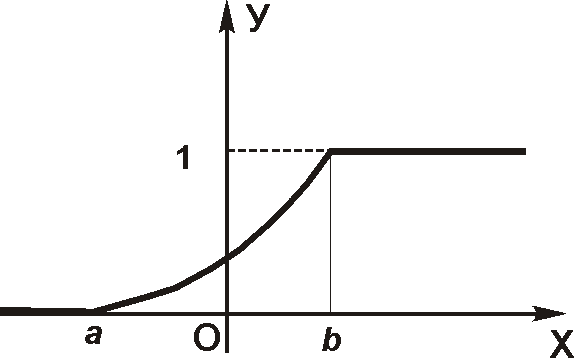
Плотность распределения вероятностей случайной величины

Определение. Плотностью распределения вероятностей непрерывной случайной величины Х (или плотностью вероятности) называют функцию - первую производную функции распределения F(х): .

Из этого определения следует, что функция распределения является первообразной для плотности распределения.. Зная плотность распределения, можно вычислить вероятность того, что непрерывная случайная величина примет значение, принадлежащее заданному интервалу.

Вероятность того, что непрерывная случайная величина Х примет значение, принадлежащее интервалу , равна определенному интегралу от плотности распределения, взятому в пределах от до : .

Свойства плотности распределения:

- плотность распределения – неотрицательная функция: ;

- интеграл от плотности распределения от -∞ до +∞ равен единице: ; в частности, если все значения случайной величины принадлежат интервалу , то .