Формула полной вероятности событий и формула Байеса

Пусть имеется полная группа несовместных событий A₁, А₂, ... , А_п, с известными вероятностями Р(А₁), Р(А₂),… Р(А_n). Событие В может наступить только при появлении одного из событий А_i, причем известны условные вероятности Р(В/А₁), Р(В/А₂),… Р(В/ _n). Найти вероятность события В по этим данным позволяет формула полной вероятности:

Р(В) = Р(А₁)· Р(В/А₁) + Р(А₂)· Р(В/А₂) + …. + Р(А_n)· Р(В/А_n).

Пусть теперь событие В может, по прежнему, наступить с одним из несовместных событий A₁, А₂, ... ,А_п, образующих полную группу. Пусть в результате какого-то из испытаний событие В произошло. Возникает вопрос, как изменятся условные вероятности событий A₁, А₂, ... ,А_п,, т.е. Р(А_i /В) в результате наступления события В?

Ответ на этот вопрос дает формула Байеса:

, где Р(В) – полная вероятность события В.

Формула Байеса широко применяется при решении проблем с недостаточной информацией: пусть имеется несколько несовместных предположений (гипотез), которые надо проверить с помощью опыта. Перед началом опыта не всегда можно определить вероятности этих гипотез, которые называют доопытными или априорными вероятностями. Этими вероятностями приходится задаваться, исходя из какого-то опыта или просто по интуиции. Как только опыт проведен, появляется информация, с помощью которой можно коррекцию априорных вероятностей.

Таким образом, основываясь на результатах опыта, заменяют априорные вероятности послеопытными (или апостериорными). После коррекции эксперимент можно продолжать (повторять опыт), продолжая уточнять вероятности гипотез.

Распределение Бернулли

Пусть в серии n независимых испытаний события А может появиться или не появиться в каждом испытании. Вероятность появления А равна , непоявления - . Случайной величиной Х объявим число появлений события А в этих n испытаниях. Значения величины Х: 0,1,2,…,n; k – номер испытания:0,1,2,…,…,n. Тогда закон Бернулли имеет вид:

.

Эта формула дает возможность вычислить вероятность появления события А в результате испытаний ровно k раз.

Распределение Пуассона.

Это распределение используется для определения вероятности того, что при очень большом количестве испытаний (массовые испытания), в каждом из которых вероятность события А очень мала (р ≤ 0,001), событие А наступит ровно k раз. В этом случае используется формула:

, где е ≈ 2,718.

Практические задания по теме 6.1

1. В урне 10 красных и 8 синих шаров. Наугад вынимают один. Какова вероятность того, что вынут шар красного цвета?

Решение. Это испытание имеет 18 равновозможных исходов. Каждый исход означает выбор одного шара. Пусть событие А означает выбор красного шара. Число исходов, благоприятных событию А, равно 10. Итак, т(А) = 10, п = 18 и

2. Монета подбрасывается два раза. Найти вероятность того, что выпадут и решка и орел.

Решение. Обозначим событие, состоящее в выпадении орла, буквой О, решки — буквой Р. Испытанием здесь является двукратное подбрасывание монеты. Всего может быть 4 исхода: ОО, РР, ОР, РО, поэтому п = 4. Событие А, состоящее в выпадении и орла и решки имеет два благоприятных исхода: РО и ОР. Следовательно, т(А) = 2, п = 4 и

3. В лотерее разыгрывается 1000 билетов. Их них 15 выигрывают по 50 000 руб., 25 — по 10 000 руб., 60 — по 5000 руб. Играющий приобрел один билет. Какова вероятность выиграть не менее 10 000 руб.?

Решение. Испытание состоит в выборе наугад одного билета из 1000. Поэтому число всех равновозможных исходов равно п = 1000. Пусть событие А состоит в том, что участник лотереи приобрел билет, который выигрывает либо 5000, либо 10 000 рублей. Число всех таких билетов равно т(А) = 40. Поэтому

4. В урне 8 белых, 5 синих и 2 красных шара. Какова вероятность того, что вынутый шар будет синего или красного цвета?

Решение. Пусть событие А состоит в том, что вынут синий шар, а событие В — вынут красный шар. Тогда Р(А) = , Р(В) = . Событие А + В означает, что вынут шар синего или красного цвета. Так как события А и В несовместны, то вероятность события А + В вычисляется по формуле:

Р(А +В) = + = .

5. Один лотерейный билет выигрывает с вероятностью 0,0001. Какова вероятность того, что владелец одного билета ничего не выиграет?

Решение. Пусть событие А означает выигрыш. Тогда означает, что билет не выигрывает. По формуле (2)

Р( ) = 1 - 0,0001 = 0,9999.

6. Бросается два кубика отдельно друг от друга. Какова вероятность того, что на первом выпадет четное количество очков (событие А), а на втором число очков будет меньше пяти (событие В)?

Решение. В данном случае ясно, что повлиять друг на друга эти события не могут – они независимы. Вероятности: Р(А)=12; Р(В)=23. Следовательно, вероятность совместного появления обоих событий: Р(АВ)=Р(А)·Р(В) = 1/2·2/3 = 1/3.

7. Из колоды карт выбирают две. Какова вероятность того, что будут вынуты 2 туза?

Решение. Пусть событие В состоит в том, что первая карта туз, а событие А — вторая карта туз. Нужно найти вероятность произведения АВ. Тогда искомая вероятность:

Р(АВ) = Р(В)Р(А/В) = • = .

8. Предполагается произвести два выстрела в цель из орудия. Необходимо оценить вероятности события В: «разрушения цели», если вероятности попадания снаряда в цель:

- 0 снарядов Р(А₀) = 1/8; - 1 снаряда Р(А₁) = 5/8; - 2 снарядов Р(А₂) = 2/8,

и вероятности разрушения цели при попадании в нее

- 0 снарядов Р(В/ А₀) = 0; - 1 снаряда Р(В/ А₁) = 2/9; - 2 снарядов Р(В/ А₂) = 5/9.

Т.к. события А₀, А₁, А₂ составляют полную группу событий, то вероятность разрушения цели:

Р(В) = Р(А₀)· Р(В/А₀) + Р(А₁)· Р(В/А₁) +Р(А₂)· Р(В/А₂) = 1/8·0+5/8·2/9+2/8·5/9=5/18.

9. По цели было произведено два выстрела. Цель была поражена. Используя данные предыдущего примера, требуется найти вероятности Р(А₀ /В), Р(А₁ /В), Р(А₂ /В) получения ровно 0, 1 и 2 попаданий.

Вероятность полного отсутствия попаданий:

.

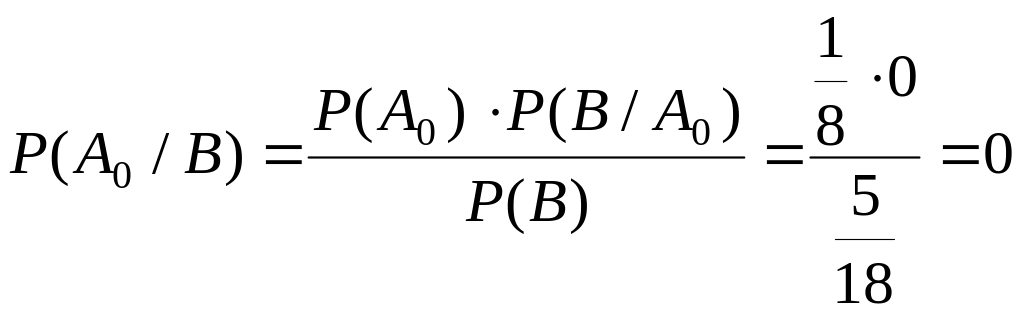Вероятность одного из двух попаданий:

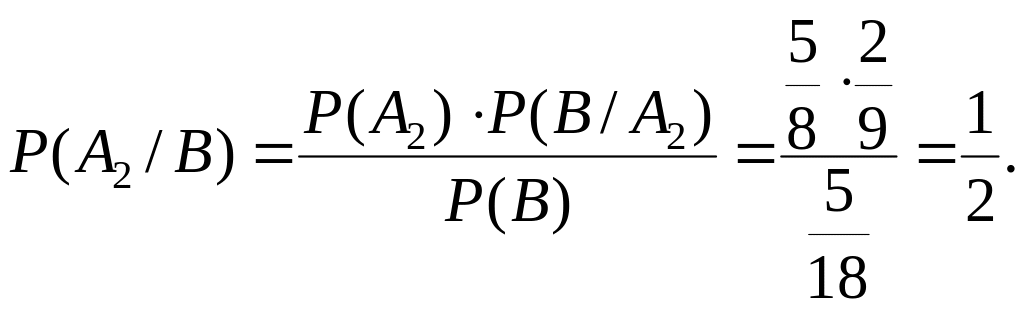
10. Производится серия из 5 выстрелов, в каждом из которых попадание возможно с вероятностью . Какова вероятность того, что из пяти выстрелов попадание будет ровно в трех?

Решение. Т.к. вероятность попадания при одном выстреле , то вероятность промаха при выстреле . Тогда вероятность ровно трех попаданий в серии из пяти выстрелов:

.

11. Произведено 5000 изделий. Вероятность того, что какое-либо изделие – бракованно, р=0,0002. Какова вероятность, что во всей партии изделий ровно три будет бракованных?

Здесь n = 5000, р = 0,0002, k = 3. Находим np = 5000·0,0002=1, тогда искомая вероятность: .