Метод интегрирования по частям

Пусть u = u(x) и v = v(x) – дифференцируемые функции. По свойству дифференциала: или . Интегрируя обе части последнего равенства и учитывая свойства неопределенного интеграла, получим:

Эта формула называется формулой интегрирования по частям для неопределенного интеграла. Для её применения подинтегральное выражение разбивается на два сомножителя u и dv. При переходе к правой части находится и . Такой прием приводит к цели, если интегрируется легче, чем .

Пример:

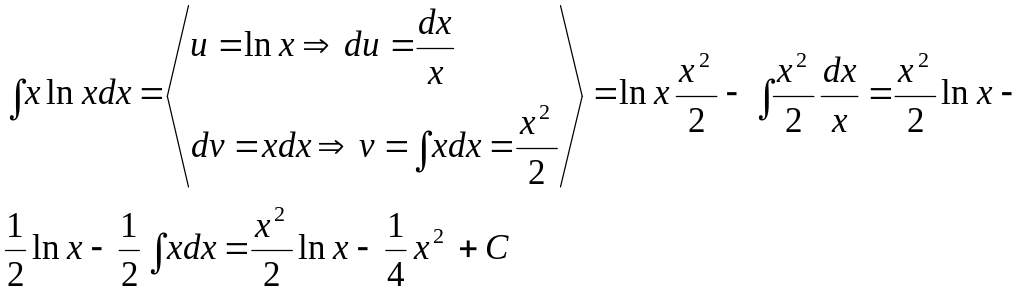Иногда для достижения результата формулу интегрирования по частям приходится применять несколько раз.

Замечание. Здесь приведены простейшие приёмы интегрирования. Если с вычисление производных проблем, как правило, не возникает, то многие интегралы не берутся в элементарных функциях или требуют громоздких вычислений. Для многих таких интегралов существуют табличные представления. Имеется ряд справочников, в которых в определенном порядке собраны наиболее распространенные интегралы.

6. Определенный интеграл Определение. Формула Ньютона - Лейбница

Пусть - функция, непрерывная на отрезке , F(х) – её первообразная, т.е. . Тогда определенным интегралом функции называется приращение её первообразной:

.

Эта формула называется формулой Ньютона-Лейбница. Здесь а и bсоответственно нижний и верхний пределы интегрирования, причем а < b.

Вычисление определенных интегралов с помощью формулы Ньютона-Лейбница осуществляется в два шага: на первом находим первообразную F(х), используя при этом технику нахождения неопределенного интеграла; на втором – используется формула Ньютона-Лейбница, т.е. вычисляются приращения первообразной, равное искомому интегралу. При это значение произвольной постоянной С не влияет на результат, поэтому при вычислении первообразной удобно сразу принять С=0. Например:

.

Формальная разница между неопределенным и определенным интегралами: Неопределенный интеграл – функция, определенный – число.

Геометрический смысл определенного интеграла состоит в том, что он численно равен площади криволинейной трапеции, образованной кривой , осью ОХ и линиями х = а и x = b, т.е. .

Свойства определенного интеграла

Все пять свойств, сформулированных для неопределенного интеграла, справедливы и для определенного интеграла. К ним добавляются следующие:

1. Интеграл, имеющий одинаковые пределы интегрирования равен нулю, т.е. .

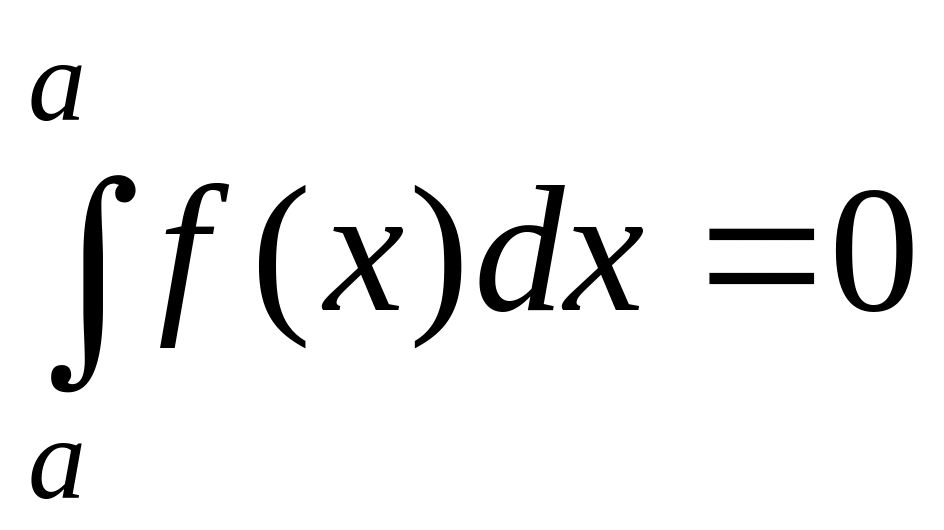2. При перестановке пределов интегрирования интеграл меняет знак на противоположный, т.е. .

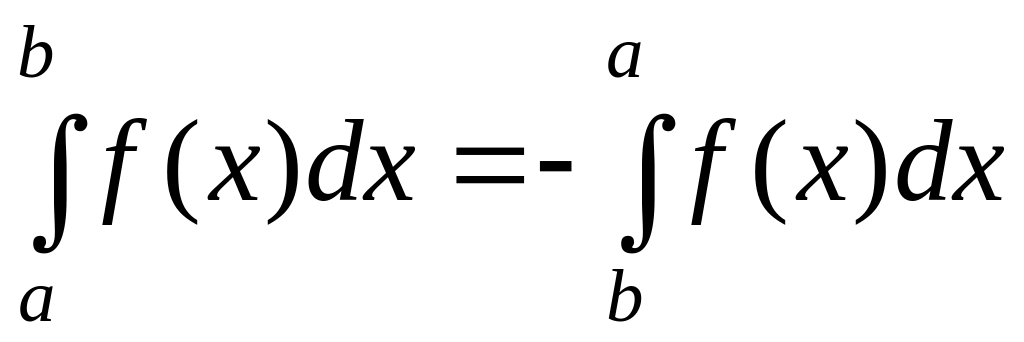3. Если интервал интегрирования разбит на части, то значение интеграла на всем интервале равен сумме интегралов по каждой из составляющих частей, т.е. при

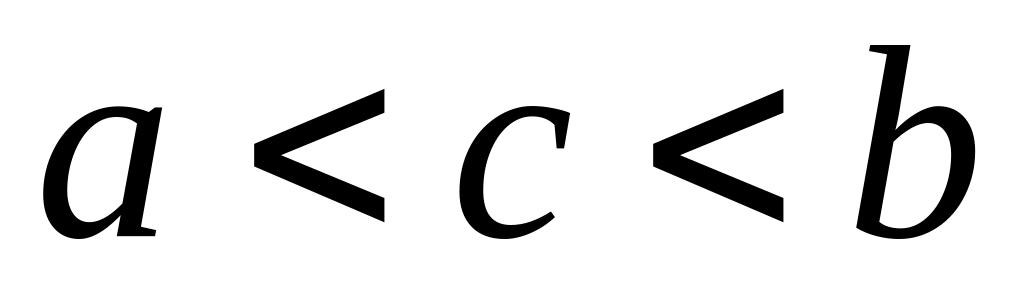
Основные методы интегрирования

Для того, чтобы вычислить определенный интеграл, достаточно найти первообразную и затем применить формулу Ньютона-Лейбница. Поэтому все методы вычисления неопределенного интеграла применимы и при вычислении определенного интеграла.

Применение определенного интеграла к вычислению площадей

Геометрический смысл определенного интеграла как площади криволинейной трапеции дает возможность применить его к вычислению любых площадей. Однако необходимо иметь ввиду, что геометрический смысл построен на формальном приписывании знаков: части функции над осью ОХ (и площади под ними) принимаются со знаком «плюс», а части функции под осью ОХ (и площади над ними) берутся со знаком «минус». Удобнее всего пользоваться формулой: 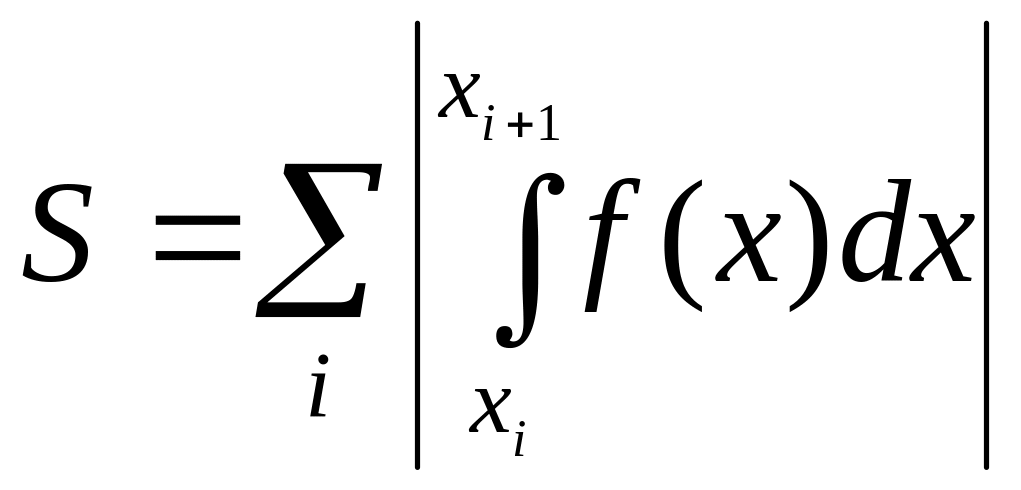, где - число подинтервалов, на которые разбивается площадь под кривой ; абсциссы на чала и конца интервала.

Определение площадей удобно проводить в два этапа. На первом решается уравнение , находится число подинтервалов и точки их начала и конца; на втором применяется формула площади. Для наглядности рекомендуется выполнить эскиз расчетной области.