Асимптоты функции

Асимптотой кривой G называется прямая L, расстояние от точек которой до кривой G стремится к нулю при неограниченной удалении от начала координат.

Существует два вида асимптот.

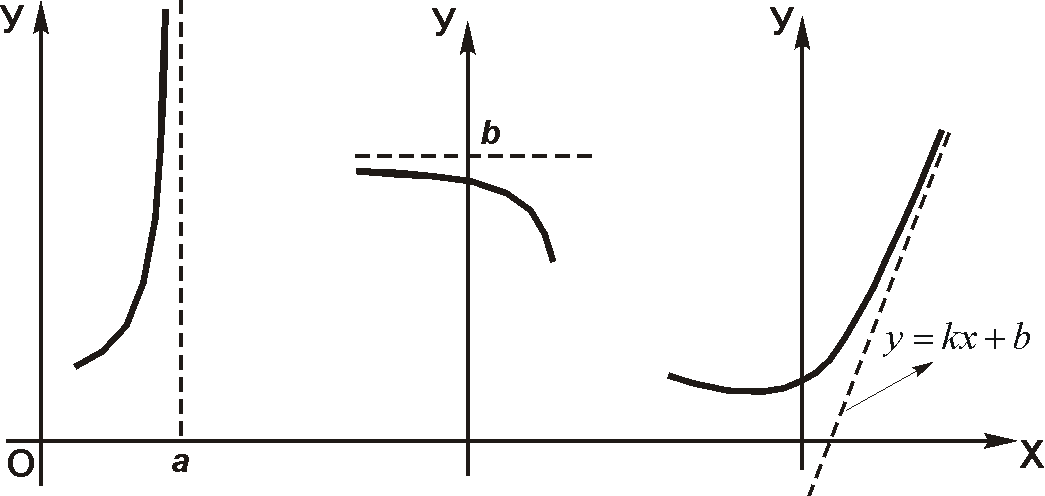
1. Вертикальные асимптоты: прямая , где а – точка, в которой функция не определена. Находятся из анализа области определения функции . Например, не определена в точке , следовательно, и есть вертикальная асимптота.

2. Наклонная асимптота имеет уравнение , где и . Если k=0, имеет место горизонтальная асимптота .

Общая схема исследования функции и построения графиков

В современных условиях построение графиков осуществляется, как правило, по точкам или с помощью компьютерных программ. Однако в задачах с повышенной ответственностью необходимо использовать исследование функции с помощью описанных выше приемов. Полная схема исследования функций и построения её графика состоит из следующих этапов:

1. Находится область определения функции .

2. Устанавливаются вертикальные асимптоты.

3. Исследуется тип функции: четная, нечетная.

4. Определяется периодичность функции.

5. Функции исследуется на наличие точек экстремума.

6. Исследуются точки перегиба функции.

7. Определяется наличие наклонных и горизонтальных асимптот.

8. Их решения уравнения определяются точки пересечения с осью ОХ. При подстановке в равнение значения х=0 определяется точка пересечения с осью ОУ.

9. При необходимости исследуется поведение функции при и при , если - вертикальная асимптота.

10. Все полученные результаты анализа функции используются для построения её графика.

Практические задания по теме 4.4

1. Вычислить пределы функции, пользуясь правилом Лопиталя:

а)

б)

2. Исследовать функцию у = х³ + 6х² + 9х +2 и построить ее график.

• Область определения х (-;), т.е. функция определена всюду.

• Исследуем поведения функции на концах области определения.

; ,

• Уравнение вертикальной асимптоты х=х₀ , где х₀ -точка, в которой функция не определена. Т. к. в наше случае функция определена всюду, вертикальных асимптот нет.

• Функция не четная и не нечетная , т.е. f(-x)  f(x) и f(-x)  - f(x).

• Функция не обладает периодичностью.

• Исследуем на монотонность и находим точки экстремум. Находим первую производную: у=3х² + 12х +9. Решая уравнение 3х² + 12х +9 = 0, находим две критические точки: х₁ = -3, х₂ = -1. Результаты исследований на монотонность и точки экстремум оформляем в виде таблицы:

х	(-; -3)	-3	(-3; -1)	-1	(-1; +-)
у у	+ возрастает	0 max f(-3)= 2	- убывает	0 min f(-1)= -2	+ возрастает

• Исследуем на выпуклость, вогнутость и точки перегиба с помощью второй производной: у=6х + 12. Критическая точка: х = -2. Результаты исследований на выпуклость и точки перегиба оформляем в виде таблицы:

  х	(-; -2)	-2	(-2; +-)
  у у	- выпуклая	0 перегиб из выпуклой в вогнутую	+ вогнутая

• Н

  

  аходим и горизонтальные наклонные асимптоты, уравнение которых: у = kх + b, где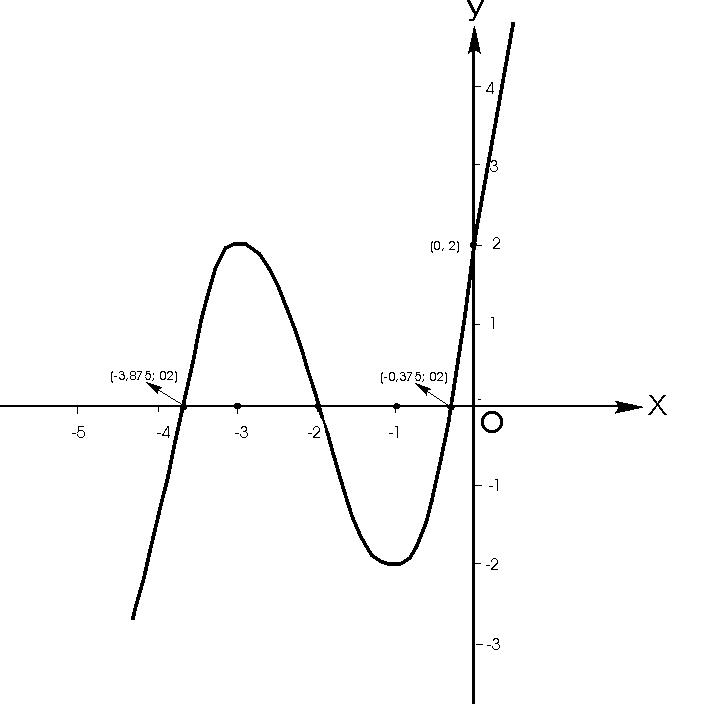 , b = [ f (x) – kx].

Следовательно, = .

Это значит, что наклонных и горизонтальных асимптот нет.

• Находим точки пересечения графика функции с осями.

- Точки пересечения с осью ОУ получаем, решая систему уравнений:

Точка пересечения графика с осью ОУ (0; 2).

- Точки пересечения с осью ОХ получаем, решая систему уравнений:

Ищем корень уравнения = 0 среди целых делителей свободного члена уравнения: 1; 2, подставляя их поочередно в уравнение. Таким корнем является х = -2 (точка перегиба). Делим выражение х³ + 6х² + 9х +2 на (х+2). В частном получаем: х² +4х +1.

Корни уравнения х² + 4х +2 =0 : х₁≈ -0,375, х₂≈ -3,875.

Таким образом, кривая пересекается с осью ОХ в точках (-2,0), (-0,375; 0) и (-3,875; 0).

В соответствии с результатами исследований, строим график (рис. 3) функции:

у = х³ + 6х² + 9х +2 .