4.4. Применения производной
Вычисление пределов по правилу Лопиталя
Часто раскрыть неопределенностей типа 0/0, ∞/∞, 0∞, ∞ - ∞, 0∞. в задачах о пределах помогает правило Лопиталя:
и
т.д.,
т.е., отношение функций заменяется отношением их производных до тех пор, пока неопределенность не исчезнет.
З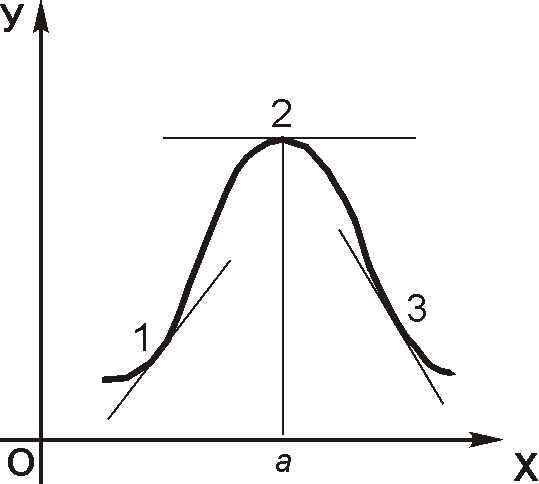
амечание.
При отсутствии неопределенности правило
Лопиталя применять нельзя!
Возрастание и убывание функции
Пользуясь геометрическим свойством производной, можно показать, что если производная функции положительна на интервале, то функция на этом интервале возрастает,
если производная отрицательна, то функция убывает. Точки, в которых производная функции равна нулю ( ) называются стационарными и часто характеризуют момент смены возрастания функции на убывание и наоборот. Таких точек на интервале может быть несколько.
Экстремумы функции
Среди
стационарных точек выделим экстремальные:
функция
имеет максимум (минимум) в точке
,
если вблизи этой точки всем значениям
х
соответствует
меньшее
(большее), чем
.
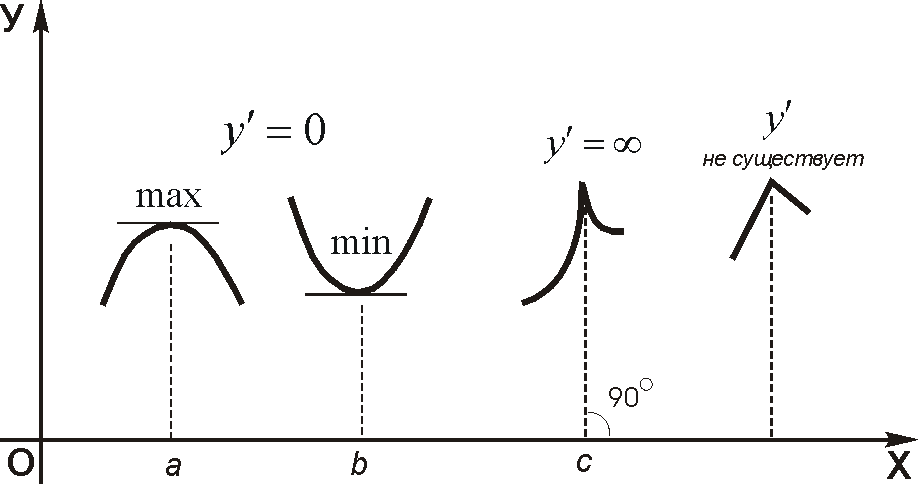
Необходимые условия экстремума:
Если
функция
имеет экстремум в точке
,
то в этой точке ее производная
либо равна нулю, либо не существует.
Выполнение необходимых условий еще не гарантируют присутствие экстремума. Кроме того. Оно не дает ответа о типе экстремума- минимуме или максимуме. Кроме того, оно может иметь место и не в экстремальных точках, что показано на рисунке.
Чтобы установить наличие и тип экстремума, следует проверить достаточные условия экстремума.
Первое достаточное условие экстремума: Если в стационарной точке производная меняет знак с плюса на минус (с возрастания на убывание) то функция в этой точке имеет максимум, если с минуса на плюс – минимум.
Иногда удобно использовать второе достаточное условие:
Если
в стационарной точке
вторая производная
положительна, то функция
в этой точке имеет минимум,
если отрицательна – максимум.
Схема определения экстремума функции :
-
определяем производную
;
-
находим стационарные точки функции из
анализа области определения производной
и уравнения
;
-
проверяем выбираем первое или второе
достаточное условие (в последнем случае
находим
;
- исследуем стационарные точки по достаточному условию, определяем наличие и вид экстремума;
-вычисляем
экстремальные значения функции
.
Результаты анализа функции на экстремум удобно представлять в виде таблице (ниже приводится в примере 1).
Замечание:
Если интервал изменения функции ограничен, часто возникает задача отыскания наибольшего и наименьшего значения функции на интервале . В этом случае не только сравнивают экстремумы на интервале, но и проверяют значения функции на концах интервала.
Т очки перегиба функции и их определение
Функция называется выпуклой на интервале , если любая секущая пересекает линию кривой функции не больше, чем в двух точка. При этом, если значения функции на этом интервале находятся выше секущей, функция является выпуклой вверх (выпуклой), если ниже секущей – выпуклой вниз (вогнутой). Точка, в которой выпуклость сменяется на вогнутость (или наоборот) называ-ется точкой перегиба функции .
Исследование функции на точки перегиба осуществляются с помощью второй производной функции по следующим правилам:
- если значения второй производная на интервале отрицательны, то функция выпукла на этом интервале;
- если значения второй производная на интервале положительные, то функция вогнута на этом интервале;
Необходимые условия для точек перегиба:
Если вторая производная функции в точке либо равна нулю, либо не существует, либо бесконечна, эта точка может быть точкой перегиба.
Если при переходе через эту точку меняет знак, то это – достаточное условие перегиба.
Схема исследования функции на точки перегиба:
- определяем производную ;
-
находим стационарные точки из анализа
области определения второй производной
и решения уравнения
;
- определяем знаки второй производной в интервалах между вычисленными точками и устанавливаем наличие точек перегиба и типы изгиба функции.
Результаты анализа функции на экстремум удобно представлять в виде таблице (ниже приводится в примере 1).