Правила дифференцирования

1. Сумма: /

2. Произведение: .

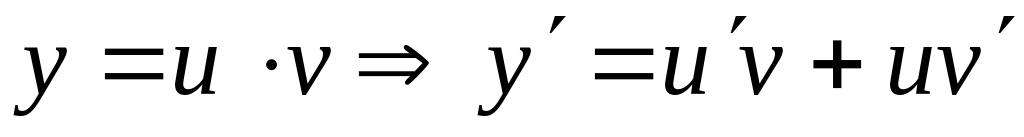3. Частное:

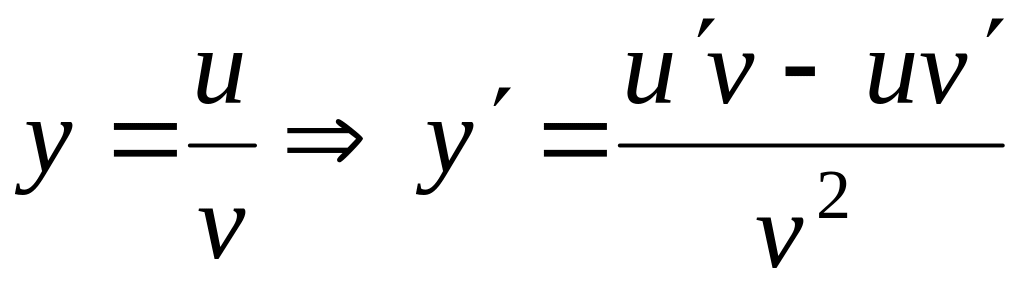
4. Постоянный множитель: .

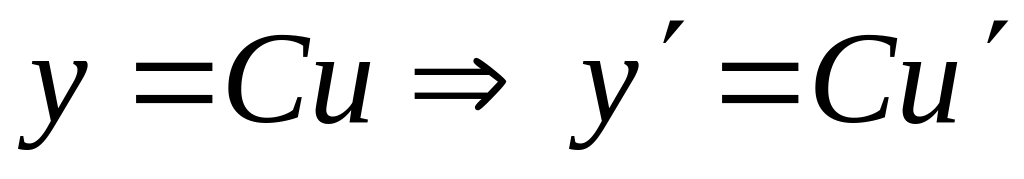5. Производная сложных функций: ;

.

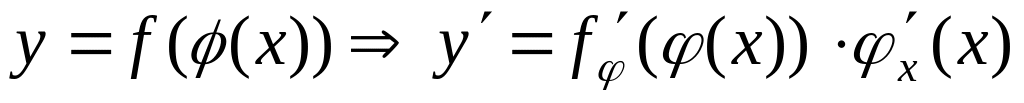Производные высших порядков

Производная определяет, очевидно, некоторую новую функцию, которую можно продифференцировать еще раз. По отношению к исходной функции это будет уже вторая производная или . Этот процесс можно продолжать и получать все более высокие производные: , , ,…, .

Только вторая производная имеет общефизический смысл – она характеризует «скорость изменения скорости» функции в точке, т.е. ускорение.

Дифференциал функции

Согласно определению производной: . Пользуясь определение предела и обозначив бесконечно малую величину , запишем: или . Так как - бесконечно малая и стремится к нулю, то вторым слагаемым можно пренебречь. Тогда первое слагаемое и называют дифференциалом функции . Для того, чтобы выделить это определение принято записывать .

Р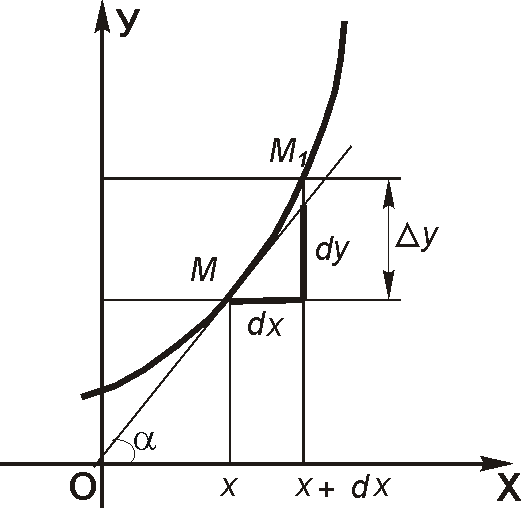 ассмотрим геометрический смысл дифференциала.

Дифференциалом функции первого порядка называется главная, линейная относительно приращения ∆х, часть приращения функции ∆у, равная произведению производной этой функции на приращение аргумента ∆х, обозначаемое в этом случае, как dx: .

Свойства дифференциала:

1. постоянная.

2. .

3. .

4. .

5.

ПРАКТИЧЕСКИЕ ЗАДАНИЯ ПО ТЕМЕ 4.3

I. Найти производные функций:

1. . Перепишем это выражение: . Теперь дифференцируем: .

2. . Используем формулу производной от произведения: .

3. . Воспользуемся формулой производной сложной функции: .

4. . Это - сложная функция. Ее производная: .

5. . Производная: .

6. . Производная:

II. Найти производные третьего порядка функций:

1. . Последовательно дифференцируя, получим: ;

;

.

2. . Последовательно дифференцируя, получим: ;

.

III. Вычислить дифференциал функции: .

.

Тренировочные вопросы по теме 4.3

Найти производную функций в точке х = 1.

1. 2. ;

Ответ: -6,2; Ответ:480;

3. ; 4.

Ответ: 11/81; Ответ:1,5/е;

5. ; 6. ;

Ответ: 4 е; Ответ: -15е^-5;

Найти вторые производные от функций в точке х = 1:

7. 8.

Ответ: 60; Ответ: 50;

9. Вычислить дифференциал функции: .

Контрольные вопросы по теме 4.3

1. Приращение функции. Производная функции. Определение.

2. Геометрический и физический смысл.

3. Табличные производные.

4. Свойства производных.

5. Производные сложных функций.

6. Производные высших порядков.

7. Дифференциал. Определение.

8. Геометрический смысл дифференциала.

9. Свойства дифференциала.

Литература. А: 1-6, 10,11; В: 7,8.