Тренировочные задания по темам 4.1, 4.2
Вычислить пределы:
1.
;
2.
;
Ответ: 3. Ответ: 0.
3.
;
4.
Ответ: 1. Ответ: 3,25.
5.
;
6.
;
Ответ: 0,125. Ответ: 1,5.
7.
;
8.
;
Ответ: е15. Ответ: 5.
9.
;
10.
;
Ответ: 0,5. Ответ: е-2.
КОНТРОЛЬНЫЕ ВОПРОСЫ ПО ТЕМАМ 4.1 и 4.2
Определение функции.
Область определения и значений функции.
Способы задания функции.
Основные элементарные функции.
Определение предела функции.
Бесконечно малые и бесконечно-большие величины. Их свойства.
Теоремы о пределах.
Вычисление пределов
Замечательные пределы.
Непрерывность функции в точке и на интервале.
Типы разрывов функции.
Свойства функции, непрерывной на интервале.
Литература. А: 1-6, 10,11; В: 7,8.
Производная и дифференциал функции Определение производной, геометрический и физический смысл
Приращением
функции
в интервале ∆х
называется разность
.
Если ∆у>0,
функция на
интервале возрастает; при
∆у<0 – убывает;
при ∆у=0 –
не меняется.
Предел отношения приращения функции ∆у к приращению аргумента ∆у при стремлении ∆у к нулю называется производной функции:
Эквивалентные
обозначения:
.
Г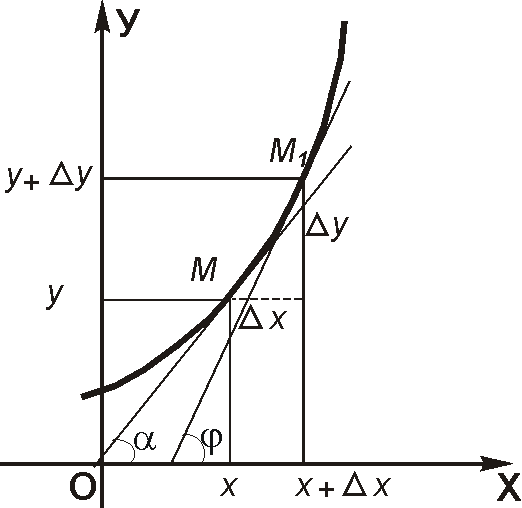
еометрический
смысл
производной связан с понятие касательной
в точке.
Проведем
через точку М секущую ММ1.
Если точку М1
устремить
к М, т.е. уменьшать ∆х,
до нуля, то
в момент слияния точек М и М1
угол φ
перейдет в угол α:
;
,
следовательно, производная функции в
точке равна угловому коэффициенту
касательной, проведенной к графику
функции в этой точке.
Физический смысл производной – скорость изменения функции в данной точке.
Если функция имеет единственную производную в точке, она называется дифференцируемой в этой точке. Функция, дифференцируемая во всех точках интервала , называется дифференцируемой в этом интервале.
Табличные производные
Пользуясь определением производной можно получить ее выражение для любых функций. На этой основе разработана и постоянно используется стандартная таблица производных:
1.
у = С
,
где С – постоянная
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
