Классификация функций

1. Основные элементарные функции:

- степенная , ;

- показательная ;

- логарифмическая 1;

- тригонометрическая sin x, cos x, tg x, ctgx$

- обратные тригонометрические arcsin x, arcos x, arctg x, arcctgx.

2. Алгебраические функции:

- целая рациональная (полином) , ;

- рациональные – отношение полиномов;

- иррациональные – наличие радикалов (дробных степеней).

3. Трансцендентные функции.

К ним относятся логарифмические, показательные, тригонометрические и смешанные функции.

4. Неявные функции.

Функция, заданная уравнением , например, .

5. Сложные функции.

Это функции составного типа или более громоздкие. Например, функция

4.2. Предел функции

Определений Коши

Ч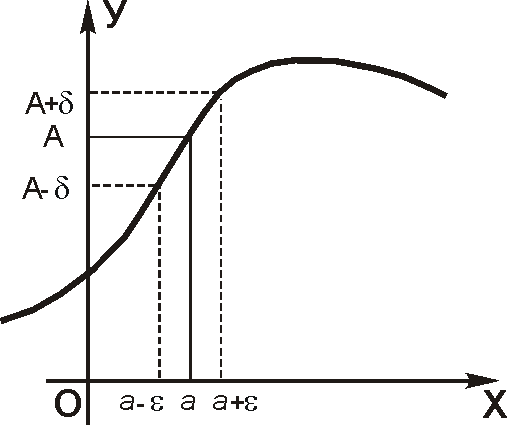 исло А называется пределом функции при , стремящемся к а (пишется или , если для любого положительного можно указать такое , что для всех , удовлетворяющих условию , выполняется (то есть, для всех , достаточно близких к а и отличных от а, значение сколь угодно мало отличается от А).

Для любого интервала всегда можно построить интервал такой, что для всех значения . Это определение предела в точке. Не требуется, чтобы .

Определение Гейне

Число А называется пределом функции при , стремящемся к а, если для все , сколь угодно мало отличающихся от а, будет сколь угодно мало отличаться от А.

Число А называется пределом при , стремящемся к бесконечности, если для любого положительного можно указать положительное число М>0, такое, что при или .

Теоремы о пределах

1. Предел постоянной равен этой постоянной: .

2. Постоянную можно выносить за знак предела: .

3. Предел суммы (разности) функций равен сумме (разности) пределов:

.

4. Предел произведения функций равен произведению пределов функций:

.

5. Предел частного функций равен частному пределов функций при условии, что предел знаменателя отличен от нуля:

.

Вычисление пределов

Наиболее общий прием, который всегда используется первым – прямая подстановка. Нахождение предела часто сводится к подстановке в исследуемое выражение предельного значения переменной, например:

Иногда подстановка предельного значения переменной приводит к выражениям вида: 0/0, ∞/∞, 0∞, ∞ - ∞, ∞⁰,1^∞, 0⁰. Такая ситуация называется неопределенностью, а вычисление пределах – раскрытие неопределенности.

Рассмотрим некоторые приемы раскрытия неопределенности.

1. Упрощение функции. К нужному результату может приводить выделение общего множителя, например:

.

.

Замечательные пределы

Ряд пределов, часто встречающихся в практике, по историческим причинам получили название замечательных.

Первый замечательный предел: .

Второй замечательный предел:

Следствия из первого и второго замечательных пределов:

1. . 2. . 3. .

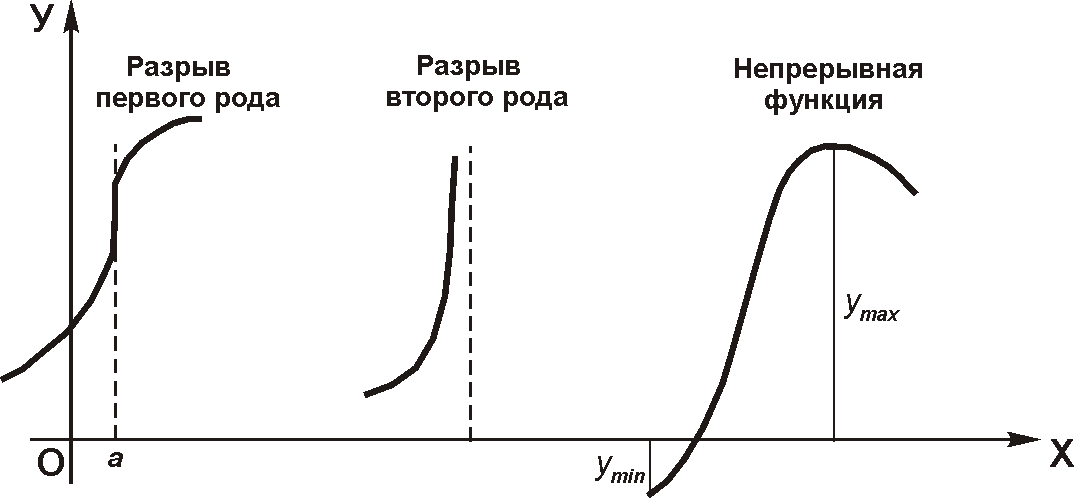
Непрерывность функции

Функция называется непрерывной в точке , если:

1. Она определена в этой точке, т.е., если существует .

1. Имеет предел в этой точке .

2. Предел совпадает со значением функции в этой точке .

Если хотя бы одно из этих условий не выполняется, то функция разрывна в точке . Этот разрыв может быть конечен – скачок (разрыв первого рода), или бесконечен (разрыв второго рода).

Функция называется непрерывной на интервале , если она непрерывна в каждой точке этого интервала. При этом:

1. Она ограничена на этом интервале сверху и снизу (не может быть бесконечного значения).

2. Обязательно имеет максимальное и минимальное значения.

3. Если на концах интервала функция имеет разные знаки, то внутри интервала имеется хотя бы одна точка х=с, в которой (корень функции).

Примеры непрерывных и разрывных функций.

- функция непрерывная всюду;

- для функции точка х = 1 – точка разрыва.

ПРАКТИЧЕСКИЕ ЗАДАНИЯ ПО ТЕМАМ 4.1, 4.2

Понятие предела позволяет прогнозировать поведение различных процессов или моделей как на бесконечности, так и в конкретных точках. На ряде примеров покажем основные приемы вычисления пределов.

Замечание1. В любой задаче на пределы сначала рассматривается прямая подстановка . Если при этом получается конечное значение (в том числе и 0) или ∞ , или - ∞, то расчет окончен.

Замечание 2. Часто для вычисления пределов удобно пользоваться теоремой: величина, обратная бесконечно большой, является бесконечно малой (т.е. 0) и величина, обратная бесконечно малой, есть бесконечно большая (т.е. ∞,).

1. .

Ответ: 13.

2. .

Ответ: 0.

3. .

Ответ: 1.

4. .

Ответ: 3.

5. .

Ответ: 0.

6. .

В этом случае следует числитель и знаменатель разделить на старшую степень аргумента, т.е. на , и использовать теорему 1/∞ = 0.

Ответ: 0.

7. . Воспользуемся первым замечательным пределом и введем замену переменных 3х=t. Если , то и . Тогда:

.

Ответ: 3.

8. .

В этом случае используется второй замечательный предел и замена . Отсюда . Если , то и .

Ответ: e^2.

9.

В этом случае используем второй замечательный предел и замену переменных:

-2х=у. Отсюда следует, если , то и .

Ответ: e^-2.