НЕГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ
ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
ТОМСКИЙ ЭКОНОМИКО-ЮРИДИЧЕСКИЙ ИНСТИТУТ
НОВОСИБИРСКИЙ ФИЛИАЛ
Кафедра гуманитарных, социально-экономических
и естественнонаучных дисциплин
Л.Н. Гахова
МАТЕМАТИКА
Учебно-методический комплекс
Новосибирск
2008
УДК 510.5
ББК 22.1
Г24
Учебно-методический комплекс рекомендован к изданию
кафедрой гуманитарных социально-экономических
и естественно-научных дисциплин
Новосибирского филиала НОУ ВПО
«Томский экономико-юридический институт»
(протокол заседания № 1 от 19 сентября 2008 г.)
УМК одобрен учебно-методическим советом
Новосибирского филиала НОУ ВПО «ТЭЮИ»
(протокол заседания №1 от 24 сентября 2008 г.)
Гахова Л.Н.
Г24 |
Математика [текст]: учебно-методический комплекс / Л.Н. Гахова. – Новосибирск: ООО «Прометей», 2008. – с. |
Данный учебно-методический комплекс включает в себя цели и задачи изучения дисциплины, методические рекомендации по изучению тем программы, выполнению контрольных заданий, задания для самоконтроля. Учебно-методический комплекс предназначен для использования в учебном процессе студентами Новосибирского филиала ТЭЮИ и может быть использован преподавателями и студентами других высших учебных заведений юридического профиля.
УДК 510.5
ББК 22.1
Ó Гахова Л.Н., 2008
ÓООО «Прометей», оформление, 2008
НЕГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ
ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
ТОМСКИЙ ЭКОНОМИКО-ЮРИДИЧЕСКИЙ ИНСТИТУТ
НОВОСИБИРСКИЙ ФИЛИАЛ
Кафедра гуманитарных, социально-экономических
и естественнонаучных дисциплин
РАБОЧАЯ ПРОГРАММА
по дисциплине
«МАТЕМАТИКА»
по направлению «Юриспруденция»
Программу подготовила
кандидат математических наук
Гахова Л.Н.
Программа одобрена
на заседании кафедры
протокол № 1 от 19 сентября 2008 года
Цели и задачи дисциплины
В последние годы в связи с интенсивным внедрением ЭВМ и методов системного анализа во все сферы гуманитарных наук, существенно повысилась значимость изучения информатики и ряда разделов математики, необходимых современному профессионалу. Эти дисциплины следует рассматривать как прикладной аппарат специалиста, освобожденный от устаревших сведений и теоретических излишеств, позволяющий решать реальные задачи и получать оценки состояния и прогнозного развития исследуемых процессов.
Эти факты определили требования Государственных образовательных стандартов в том, что информатика и математика являются обязательными учебными дисциплинами при подготовке специалистов юридического профиля, усилено внимания к качеству образования по указанным дисциплинам.
Курс математики в НФ ТЭЮИ обеспечивает выполнение следующих образовательных задач:
Освоение базовых разделов математики, необходимых для анализа и моделирования профессиональных задач.
Овладение прикладными расчетными приемами по реализации вычислительных аспектов математических задач.
Определение и упорядочение необходимого объема информации при постановке, реализации и обработке результатов решения математических задач.
Умение пользоваться справочной и специальной литературой, соответствующей конкретной проблеме.
Данный учебно-методический комплекс (УМК) содержит темы, соответствующих принятой в НФ ТЭЮИ программе дисциплины Математика. По каждой теме приводится необходимый теоретический материал, практические задания и примеры решения задач, тренировочные задания, контрольные вопросы и список рекомендованной по теме литературы. Последовательность изучения и изложения в данном пособие тем и их содержание определяется учебной программой дисциплины.
Основной целью курса математики является формирование способности студента к самостоятельному мышлению и умению применять изучаемые разделы для решения конкретных задач. Особое внимание студенту следует уделить отработке расчетных навыков, пониманию алгоритмов раскрытия математических задач и умению объяснять и обосновывать полученные решения. Студент должен не только ясно представлять какое-либо теоретическое положение, но и его практический смысл, схему использования теории в модельных расчетах.
В конце УМК приведены вопросы для подготовки и сдачи экзамена по дисциплине.
Необходимо помнить, что основным навыком профессионала является умение самостоятельно работать с литературой в процессе решения конкретной проблемы. Учебно-методический комплекс позволит сосредоточить внимание только на тех разделах и той теории, которые необходимы профессионалу. Изучение приведенной в конце каждой темы пособия литературы позволит дополнить информацию как с содержательной стороны так и практическими примерами.
Общий список литературы приведен в конце пособия. В каждой главе указаны рекомендуемые по теме источники из общего списка литературы.
Содержание курса
1. Линейная алгебра
1.1. Система линейных алгебраических уравнений (слау).
Определение 1.
Системой s линейных алгебраических уравнений с n неизвестными называются соотношения вида:
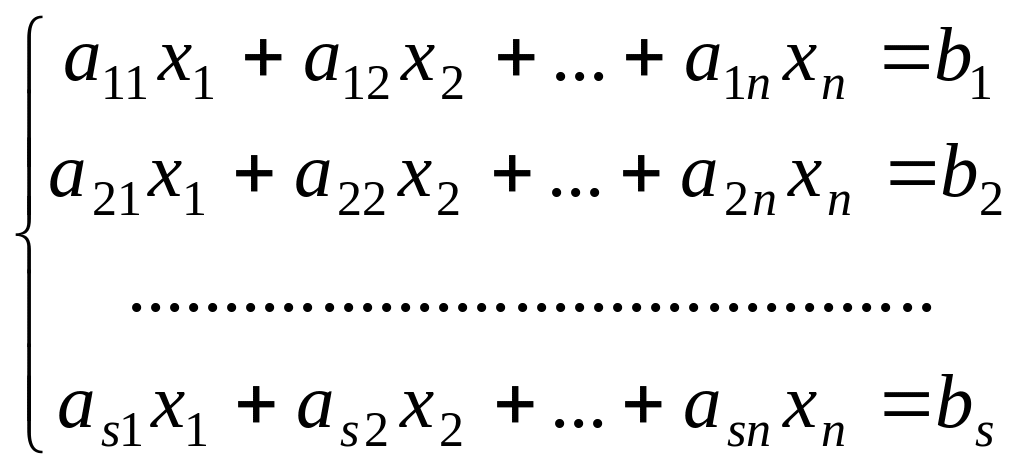(1.1)
Здесь
величины
называются неизвестными
системы; числа
- коэффициентами при неизвестных или
коэффициентами системы; числа
свободными членами.
Определение
2. Решением
системы (1.1) называется совокупность
чисел
,
которые при подстановки в систему все
уравнения обращают в тождества.
Определение 3. Система называется совместной, если она имеет хотя бы одно решение, и несовместной, если она не имеет ни одного решения.
Определение 4. Система называется определенной, если она имеет единственное решение, и неопределенной, если имеет более одного решения.
Определение 5. Две системы называются эквивалентными, если любое решение одной из них, является одновременно решением другой.
Все несовместные системы считаются эквивалентными.
Составим из коэффициентов системы (1.1) таблицу А и назовем ее матрицей системы:
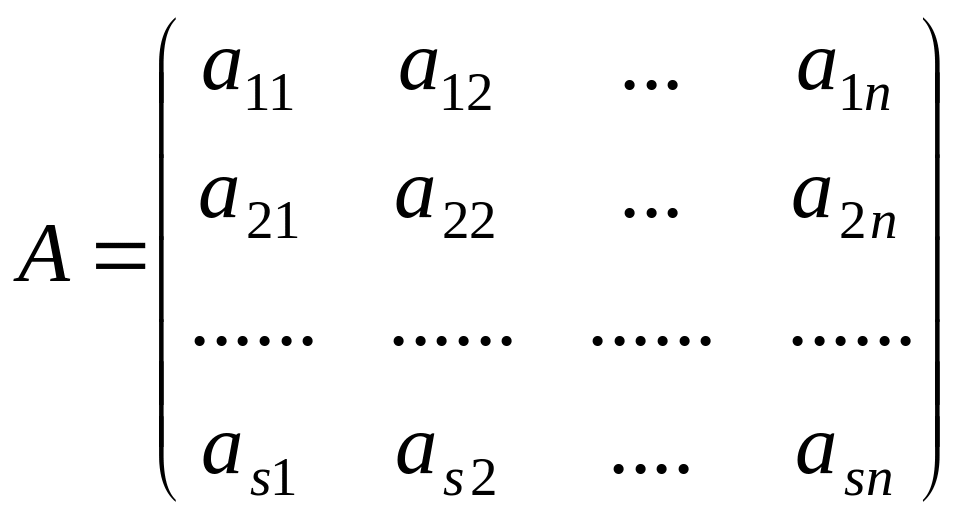(1.2)
Матрица А с добавленным справа столбцом свободных членов называется расширенной матрицей системы линейных уравнений:
(1.3)