0. Управление запасами с учетом издержек на производство

В этом параграфе мы рассмотрим модель, в которой наряду с издержками, связанными с запасами, учитываются затраты на производство самой продукции.

Некоторая фабрика производит определенный вид продукции, для хранения которой имеет свой собственный склад. Продукция может предназначаться как для внешних потребителей, так и для самой фабрики. Обозначим через спрос на эту продукцию, возникший в течение периода (дня, недели и т.д.). Если в начале года уровень запасов на складе равнялся , то после первого периода (при отсутствии пополнения) он упадет до уровня , после второго – до и т.д. Может оказаться так, что запасы исчерпываются и в этом случае будем учитывать неудовлетворенные требования, т.е. фактически введем понятие отрицательных запасов.

Предположим, что уровень производства данной продукции на период должен быть установлен до того, как становится известным спрос на этот период. Обозначим через количество единиц продукции, произведенной в -ый период. Естественно, что отклонения от могут быть значительны, и это повлияет на политику управления запасами.

Рассмотрим следующую стратегию: уровень производства в -ый период всегда равняется спросу в -й период.

.

Если в течение первой недели произведено единиц товара, то легко видеть, что уровень запасов в конце периода равняется . Трудности, связанные с реализацией такой стратегии очевидны. Производство должно очень гибко реагировать на флуктуации спроса, что влечет за собой больше издержки. Возникают проблемы с занятостью рабочих в периоды низкого спроса, со сверхурочными работами и т.д.

Альтернативная, вторая стратегия, заключается в следующем: уровень производства в период равняется математическому ожиданию спроса в период.

.

Если все случайные величины имеют одно и то же среднее ,

.

В этом случае производство всегда остается на одном и том же уровне, поэтому трудностей, типичных для предыдущей стратегии, здесь нет. Но при этом возникнут трудности, связанные с большими флуктуациями остатков относительно . В самом деле, если все имеют одну и ту же дисперсию , то остатки продукции (положительные в случае избытка и отрицательные в случае дефицита) в конце -го периода имеют дисперсию.

.

При »1 дисперсия может стать как угодно большой. Заметим, что в первой стратегии

.

Поэтому во второй стратегии могут возникнуть большие издержки, связанные с хранением запасов и дефицитом.

Можно предположить еще одну политику управления запасами, которая в некотором смысле будет компромиссом между двумя первыми. Эту стратегию естественно называть стратегией экспоненциального сглаживания.

Пусть

,

где называется константой сглаживания, . При мы получаем 2-ой случай, при – первый. Параметры являются варьируемыми переменными:

Справедливы следующие рекуррентные соотношения:

,

.

Отсюда

,

.

Видно, что при является взвешенным средним от значений спроса в течение всего прошедшего времени, причем вес слагаемого задается выражением , т.е. экспоненциально убывает с ростом . Как и в первой стратегии, уровень производства реагирует на колебания спроса, но в отличие от 1-го примера эта реакция носит более сглаженный характер.

Изучим стратегию экспоненциального сглаживания в предположении, что случайные величины не зависят друг от друга и имеют нормальное распределение со средним и дисперсией .

Тогда, как легко видеть, являются нормальными случайными величинами, при этом

,

.

В пределе средние и дисперсии случайных величин будут сходиться к значениям:

,

.

Случайные величины также нормально распределены. При этом

,

,

.

.

Введем меру, оценивающую изменения уровня производства:

.

Если , то , и поэтому

.

Отсюда видно, что если , то , и поэтому вероятность возникновения неудовлетворенных требований увеличивается. Но при этом колебания уровня производства становятся незначительными.

Пусть, как обычно, величина характеризует удельные издержки по содержанию запасов, характеризует издержки, связанные с наличием неудовлетворенных требований. В общие издержки необходимо включить затраты, связанные с колебаниями уровня производства – соответствующий коэффициент обозначим через . Тогда мы можем написать

.

Здесь предполагаем, что , и поэтому средний уровень запасов . Учтено также то обстоятельство, что в пределе имеет нормальное распределение с параметрами .

При оптимизации зафиксируем предварительно параметр , и продифференцируем по :

.

Отсюда следует, что если

,

то , в противном случае

.

Подставим в , получим

.

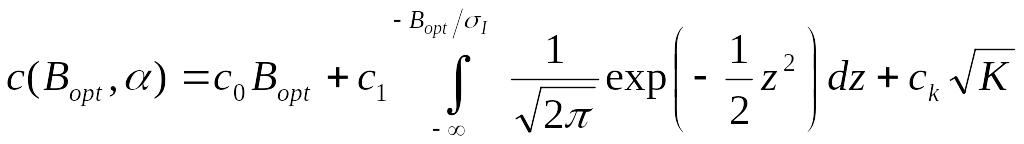Минимизация по может быть проведена численными методами.

Отметим, что более точно издержки по содержанию запасов учитываются следующим образом: вместо надо подставить величину

.

Но в этом случае минимум по с самого начала надо искать численными методами.

Задачи

1. Пусть себестоимость производства одной единицы продукта равна руб., розничная цена одной единицы продукта в сезон равна руб. По окончании сезона остатки продукции могут быть распроданы по сниженной цене руб. за единицу. Спрос на продукт в течение сезона имеет функцию распределения . Постройте функцию издержек и вычислите оптимальный уровень запасов, исходя из критерия среднего значения.

2. Цена батона в универсаме равна 10 руб. при закупочной цене 7 руб. за один батон. Спрос на батон имеет показательное распределение со средним значением единиц в день. Менеджер, отвечающий за торговлю хлебом, исходит из ошибочного предположения, что спрос имеет показательное распределение со средним значением единиц. Каковы будут средние потери в прибыли, если менеджер при расчете запасов исходит из критерия оптимизации средней прибыли?

3. Запас некоторого химического вещества на складе равен 100 кг. Стоимость хранения одного кг вещества в течение месяца равняется руб. Потери от нехватки 1 кг сырья равны руб. Стоимость подачи заказа равняется 200 руб., а стоимость закупки 1 кг этого сырья равна 50 руб. Количество вещества в килограммах, используемого в течение месяца, равномерно распределено в интервале . Какое количество сырья нужно закупить?

4. Фирма продает в течение года в среднем 5000 упаковок стирального порошка. Спрос на этот товар в течение года имеет равномерное распределение в интервале . Цена подачи заказа равна 3000 руб., закупочная цена одной упаковки равна 150 руб., стоимость хранения одной упаковки в течение года составляет 20% от цены. Время исполнения заказа равно 2 неделям. Менеджеры фирмы считают, что один случай дефицита обходится фирме в 250 руб. (потеря хорошего отношения клиента к фирме и затем потеря самого клиента). Каковы оптимальные значения размера заказа и точки подачи заказа ? Какова вероятность возникновения дефицита?