Вероятностные модели управления запасами
2.1. Одноэтапная модель управления запасами
Рассмотрим классическую задачу управлениями запасами, которую называют еще задачей о торговце газетами, или задачей о рождественской елке. Пусть есть товар, который можно продать только в течении какого-то периода времени. К концу этого периода товар либо испортится, либо станет никому не нужным (вчерашние газеты, елки после Нового года).
Спрос на товар
является случайной величиной с известным
законом распределения. Заказывать товар
можно только к началу периода (сезона).
Обозначим через
потери, которые мы понесем от одной
единицы нереализованного товара. Пусть
обозначает потери, которые мы понесем
при отсутствии одной единицы товара в
случае, когда спрос превысит предложение.
Обозначим через
количество товара, которое мы запасли
перед началом периода. Тогда функция
потерь (или издержек) примет вид:
(2.1)
В терминах первой главы обозначает наше действие, – состояние среды.
Рассмотрим сначала случай, когда товар штучный. Спрос является дискретной случайной величиной, – целочисленная переменная. Критерий среднего значения ставит задачу минимизации функции.
,
где
.
Предположим, что
функция
достигает минимума в одной точке
.
Условие на минимум в дискретном случае
запишется как
.
(2.2)
Рассмотрим разности
:
.
Поскольку
и
,
то
,
где
– функция распределения случайной
величины
.
Тогда условия (2.2) запишутся как
.
(2.3)
Мы получим не вполне очевидный ответ для такой простой задачи.
Рассмотрим теперь
случай непрерывного случайного спроса
с плотностью
.
Среднее значение функции издержек
(2.1) запишется как
.
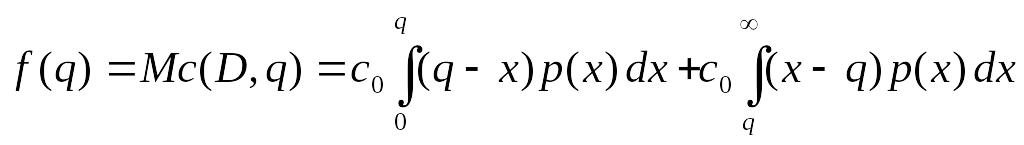Тогда
.
Приравнивая эту производную к 0, получаем, что оптимальный запас находится из уравнения
.
(2.4)
В силу монотонности
и непрерывности функции
ясно, что уравнение (2.4) имеет решение.
Тот факт, что это решение дает минимум
функции издержек, следует из того, что
.
Пример. Посредническая фирма скупает у дирекции спортивного комплекса билеты для проведения концерта по цене 500 руб. за штуку и собирается продавать их по цене 800 руб. Статистика показывает, что спрос на билеты имеет нормальное распределение с математическим ожиданием 4000 и стандартным отклонением 300. Сколько билетов стоит выкупить этой фирме?
Цена покупки
рублей.
В случае, когда спрос превысит предложение,
недополученная прибыль от одного билета
равна
800
руб.-500 руб.=300 руб. Мы должны решить
уравнение
,
где
,
где
–
функция распределения стандартного
нормального распределения
.
Так как
квантиль нормального
распределения
,
то
.
Заметим, что нормально распределенная величина может принимать и отрицательные значения, но в нашем случае это не приводит к противоречиям, поскольку вероятность такого события очень мала.
Константу можно интерпретировать как издержки, связанные с хранением единицы нереализованной продукции. Издержки, связанные с дефицитом товара, очень трудно оценить. В предыдущем примере эти издержки интерпретировались как недополученная прибыль. Когда речь идет о системе управления запасами на производстве, дефицит запчастей может привести к простою и соответствующим убыткам или к штрафным санкциям со стороны заказчиков.
В том случае, когда оценка издержек дефицита затруднительна, иногда запас определяют исходя из требования, чтобы вероятность возникновения дефицита не превышала заданной вероятности :
.