Стохастическое программирование
В последующих главах пособия будут изучаться различные стохастические модели исследования операций. При анализе этих моделей мы будем использовать в основном методы элементарной теории вероятностей и математического анализа.
Но известно, что многие задачи исследования операций могут быть сведены к задачам линейного программирования. Существует целое направление в современной науке, называемое стохастическим программированием, которое изучает вероятностные версии задач математического программирования. Алгоритмы решения задач стохастического программирования достаточно громоздки и часто приводят к решению задач линейного программирования большой размерности. Поэтому мы ограничимся лишь кратким обсуждением простейших примеров.
Предположим, что задача линейного программирования имеет вид:
(1.2)
при ограничениях
,
(1.3)
,
(1.4)
,
(1.5)
где векторы
и
,
а также матрица
являются случайными, а матрица
и вектор
–
не случайными. Предположим, что закон
распределения всех случайных величин
известен.
Если случайными
величинами являются только коэффициенты
целевой функции
,
то критерий среднего значения предлагает
искать максимум линейной функции
при тех же неслучайных ограничениях (1.3) – (1.5).
Но в общем случае
задача (1.2) – (1.5) существенно сложнее.
Простой рецепт, состоящий в том, чтобы
заменить все случайные коэффициенты
на их средние значения, может привести
к противоречию. Например, решение такой
«усредненной» задачи может не удовлетворять
ограничениям ни при каком наборе значений
коэффициентов
.
Один из возможных подходов к постановке задач стохастического программирования состоит в том, чтобы условия (1.2) – (1.5) заменить на условия
(1.6)
при ограничениях
,
(1.7)
, (1.8)
, (1.9)
где
–
заданные вероятности. Другой вариант
– вместо выполнения
условий (1.7) потребовать выполнение
одного условия
,
.
Рассмотрим следующий
пример. Фирма владеет
единицами некоторого сырья, из которого
можно изготовить два вида продукции.
Спрос на 1-ый вид обозначим
,
на 2-ой–
,
и
являются случайными величинами с
известными законами распределений. Из
одной единицы сырья можно получить
единиц продукции 1-го вида и
единиц продукции 2-го вида. Руководство
фирмы хочет максимизировать прибыль,
но при условии, что вероятности сбыта
продукции были больше заданных
вероятностей
и
.
Задача с вероятностными ограничениями
имеет вид:
(1.10)
при ограничениях
,
(1.11)
,
(1.12)
,
(1.13)
.
(1.14)
Здесь
и
–
цена продукции 1-го и 2-го вида соответственно.
Пусть
и
имеют нормальное распределение,
~
,
~
.
Тогда
.
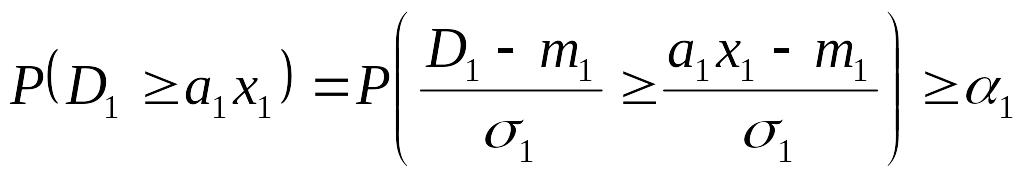(1.15)
Пусть
–
-
квантиль стандартного гауссовского
распределения:
.
Тогда условие (1.15) означает, что
или
.
(1.16)
Аналогичное условие
возникает на
:
.
(1.17)
Возникает простая задача линейного программирования, задаваемая условиям (1.10), (1.13), (1.14), (1.16), (1.17).
В случае, когда коэффициенты матрицы также являются случайными величинами с многомерным нормальным распределением, вероятностные ограничения вида (1.17) приводят к квадратичным неравенствам. Рассмотренный выше пример модели с вероятностными ограничениями относится к классу так называемых одноэтапных стохастических моделей. В одноэтапных задачах мы принимаем решения за один этап, исходя из критерия среднего значения и информации о распределениях вероятностей случайных параметров, входящих в условия задач.
Существует другой класс моделей стохастического программирования, называемых двухэтапными моделями. Рассмотрим конкретный пример такой постановки.
Имеются посевные
площади размером в
га и мы выращиваем на них две посевные
культуры, например, зерно и картофель.
Для внутренних потребностей хозяйства
(корм для скота и прочее) нам нужно
тонн зерна и
тонн картофеля. Если зерна не хватает,
то мы должны купить его на стороне по
цене
рублей за тонну, а если образуются
излишки, то сможем продать по цене
.
Для картофеля соответствующие цены
равны
и
.
Затраты на выращивание зерна равны
рублей на гектар, затраты по выращиванию
картофеля –
рублей на гектар. Урожайность этих
культур зависит от климатических
условий. Статистические данные за
прошлые годы и консультации у специалистов
дают нам следующую информацию: будущий
сезон будет нормальным с вероятностью
,
плохим – с вероятностью
и хорошим – с вероятностью
.
Пусть урожайность по зерну при нормальных
условиях равна
тонн с гектара, при плохих –
,
при хороших –
тонн с гектара. Аналогичные величины
для картофеля обозначим через
.
Введем переменные:
и
– площади, отведенные под зерно и
картофель соответственно,
и
– количество зерна или картофеля,
которое придется закупить в случае
нехватки в сезоне, находящемся в состоянии
,
и
– излишки зерна и картофеля, которые
можно будет продать в сезоне, находящемся
в состоянии
.
Поставим задачу двухэтапного стохастического программирования:
(1.18)
при ограничениях
,
(1.19)
,
(1.20)
,
(1.21)
,
(1.22)
,
(1.23)
,
(1.24)
,
(1.25)
.
(1.26)
В такой постановке имеются три возможных «сценария» – нормальный, плохой и хороший. Есть переменные, общие для всех трех сценариев – и . С каждым сценарием связаны свои переменные, которые играют роль компенсирующих переменных. Решения принимаются в два этапа. На первом этапе решается вопрос о том, какие площади и отдать под зерно и картофель. Например, и находятся из решения задачи линейного программирования (1.18) – (1.26). После того, как сезон подойдет к концу, можно будет понять, надо ли закупать зерно или картофель или наоборот, останутся излишки. Пусть, например, сезон оказался хорошим. В этом случае надо будет решить задачу:
(1.27)
при ограничениях
, (1.28)
,
(1.29)
(1.30)
(здесь и уже известны).
Таким образом, на
втором этапе можно будет обнаружить
«невязки» и компенсировать их с помощью
набора переменных
.
Конечно, выбор переменных 1-го этапа
и
должен быть таков, что задача 2-го этапа
(1.27) – (1.30) имела решение.
Переменные предварительного плана и можно находить также исходя из «усредненного» сценария. Вычислим средние урожайности по зерну и картофелю:
,
и решим задачу ЛП для этих средних значений:
(1.31)
при ограничениях
,
(1.32)
,
(1.33)
.
(1.34)
Далее ждем окончания сезона. Если он оказался, например, хорошим, решаем задачу (1.27) – (1.30), используя вместо переменных и значения, полученные при решении «усредненной» задачи (1.31)–(1.34).
Очевидным недостатком двухэтапных моделей является резкий рост размерности задачи при увеличении количества сценариев.
Задачи
1.. Придумайте пример матрицы потерь, для которой критерии Вальда, Лапласа и Сэвиджа дают разные ответы.
2. Устройство состоит из блоков, надежность каждого из них равна . Выход из строя одного блока выводит из строя все устройство. Для повышения надежности системы решено провести дублирование с помощью дополнительных блоков. Какой способ дублирования дает большую надежность: а) дублирование каждого блока; б) дублирование всей системы?
а
б
3. Рассмотрите пример простой задачи линейного программирования со случайными коэффициентами. Найдите решение «усредненной» задачи ЛП, в которой все коэффициенты заменены на их средние значения. Постройте пример задачи, в которой решение «усредненной» задачи не удовлетворяет условиям ни при каком наборе значений случайных коэффициентов.
4. Фирма изготавливает
продукцию двух видов, цены на которые
образуют случайный гауссовский вектор
со средними значениями
рублей,,
рублей и матрицей ковариаций
Затраты на производство продукции 1-го и 2-го вида равны 40 и 50 рублей соответственно. При каких минимальных затратах на производство доход продажи продукции превысит 100000 рублей.
5. Рассмотрите конкретный числовой пример для задачи о зерне и картофеле (двухэтапная стохастическая модель). Просчитайте модель (1.18) – (1.26) и (1.31) – (1.346). Сравните полученные результаты при различных сценариях.
6. Прогноз спроса на некоторый товар следующий: с вероятностью 0,6 он будет равен 1000 ед., с вероятностью 0,4 – 1500 единиц. Фирма может сама производить этот продукт по цене 3000 рублей за штуку или импортировать по цене 5000 рублей за штуку. Фирма обязана удовлетворить спрос, но стремится минимизировать издержки. Постройте двухэтапную модель стохастического программирования для этой задачи и решите ее.