7.5. Метод Монте Карло марковских цепей. Метод отжига в задачах комбинаторной оптимизации

В различных приложениях, использующих метод статистического

моделирования, часто возникает следующая задача. Имеется набор положительных чисел и надо смоделировать распределение вероятностей вида

,

где – нормирующий множитель. При этом сумму невозможно вычислить явно (например, из-за того, что очень велико). Это означает, что мы фактически не знаем значений , а можем вычислить только отношения вида .

Идея, состоит в том, чтобы построить марковскую цепь с матрицей переходных вероятностей таким образом, чтобы распределение являлось предельным распределением для этой цепи.

Пусть является однородной марковской цепью с дискретным временем и конечным множеством состояний и матрицей переходных вероятностей . Распределение вероятностей на называется обратимым для марковской цепи , если выполняются уравнения баланса:

для всех и . (7.23)

Заметим, что если выполнено условие (7.23), то распределение является стационарным для марковской цепи. Действительно,

,

т.е. .

Алгоритмы, которые моделируют заданные распределения с помощью марковских цепей, называются Монте Карло алгоритмами марковских цепей ( Markov Chain Monte Carlo – MCMC). Приведем один из наиболее общих алгоритмов МСМС – алгоритм Метрополиса-Хастингса.

Пусть . Определим следующим способом:

Шаг 1. Моделируем номер кандидата на следующее состояние с помощью некоторого распределения . Распределение должно удовлетворять условиям

а) если , то ,

б) должно задавать матрицу переходных вероятностей неразложимой марковской цепи на .

Шаг 2. Мы полагаем с вероятностью и полагаем с вероятностью , где

.

Таким образом, матрица переходных вероятностей для цепи имеет вид

.

Покажем, что распределение обратимо для цепи :

. (7.24)

Пусть, например, и . Тогда

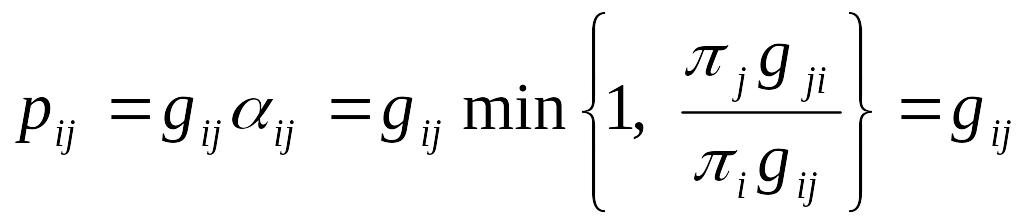. (7.25)

Также

. (7.26)

Из (7.25) и (7.26) следует (7.24).

Если матрица удовлетворяет условиям теоремы о предельных вероятностях (гл.3), то стационарное распределение является предельным распределением для этой цепи. Таким образом, выбирая любое начальное состояние и генерируя достаточно большое количество шагов эволюции этой цепи, мы можем рассчитывать на то, что с большой точностью

.

В качестве примера построим матрицу переходных вероятностей для моделирования пуассоновского распределения

.

Пусть . Промоделируем :

Шаг 1. Положим

То есть, кандидат на следующее состояние выбирается с равной вероятностью из состояний .

Шаг 2. Мы принимаем с вероятностью

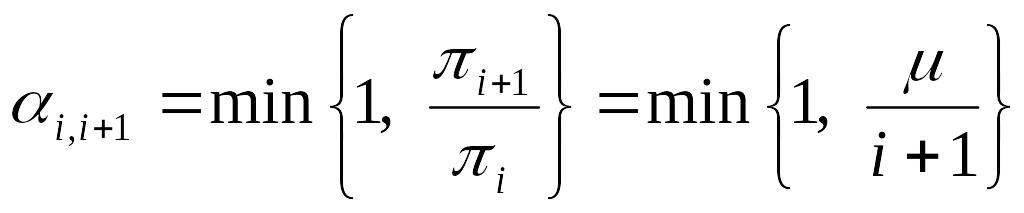
и принимаем с вероятностью

.

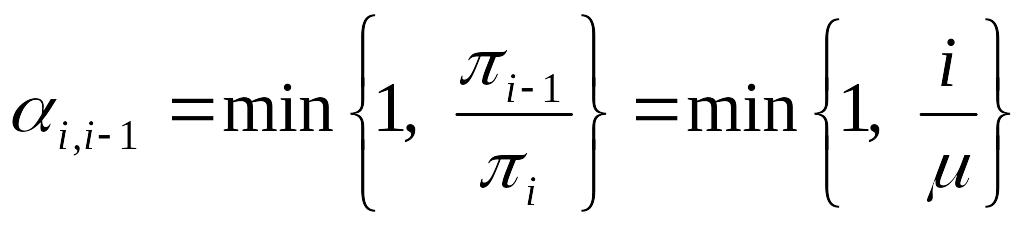Если , то состояние отвергается и принимается .

Одним из наиболее известных применений алгоритмов МСМС является метод отжига в задачах комбинаторной оптимизации. Предположим, что имеется сложная задача комбинаторной оптимизации (например, задача коммивояжера). Это значит, что мы имеем очень большое (конечное) множество вариантов , и функцию

,

которую мы хотим минимизировать. Пусть .

.

Определим распределение вероятностей на

, (7.27)

.

Здесь – вещественный параметр. В литературе иногда параметр называется температурой, функцию – энергией, распределение – распределением Больцмана (или Гиббса). Терминология пришла из статистической физики, в которой метод отжига был придуман. Сам алгоритм отжига имеет аналогию с процедурой закаливания материалов в металлургии.

Рассмотрим предельные распределения

,

.

Предложение 7.3. Распределения и являются равномерными распределениями на и соответственно:

(7.28)

. (7.29)

Доказательство.

.

Если , то и . Если , то и . Значит, при

.

Если , то выбирая , получаем

.

Похожие рассуждения доказывают (7.29).

Применим алгоритм Метрополиса-Хастингса к моделированию . Для каждой точки определим окрестность со следующими условиями:

1. 

2. для любых и тогда и только тогда, когда

3. для любых и существует и такие, что

.

Распределение определим как для и для . Тогда марковская цепь задается матрицей переходных вероятностей

Заметим, что матрица удовлетворяет условиям теоремы о предельных вероятностях. Действительно, из свойств окрестностей следует, что из любого состояния можно попасть в любое состояние за конечное число шагов, т.е. цепь является неразложимой. Кроме того, если функция не является константой, то легко видеть, что существует такое, что . Отсюда следует, что существует такое, что мы можем из любого состояния попасть в любое состояние за шагов с ненулевой вероятностью.

Алгоритм отжига является эвристическим алгоритмом, основанным на аналогии с процедурой закаливания металла. Известно, что медленное охлаждение металлического листа приводит к большей прочности материала по сравнению с процедурой быстрого охлаждения. Обычная процедура локального поиска в сложных задачах комбинаторной оптимизации приводит к тому, что мы спускаемся в какой-то локальный минимум, из которого уже не можем выйти. В то же время сложная задача комбинаторной оптимизации обычно имеет большое количество локальных минимумов, далеко отстоящих от глобального минимума. Алгоритм моделирования гиббсовского распределения (7.27) позволяет нам выскакивать из локального минимума с некоторой вероятностью и продолжить поиск.

Алгоритм отжига сводится к следующим шагам:

Шаг 1. Выбирается большое значение параметра (температуры), начальное значение и моделируется случайное блуждание алгоритма Метрополиса-Хастингса для получения гиббсовского распределения (7.27).

В силу предложения 7.3. распределение (7.27) при больших значениях близко к равномерному. Случайное блуждание легко преодолевает «энергетические» барьеры между локальными минимумами и позволяет свободно двигаться по всему пространству в поисках очередного решения.

Шаг 2. Температура снижается до значения , в качестве стартового значения выбирается то значение , на котором было остановлено случайное блуждание при температуре . Опять используется алгоритм Метрополиса-Хастингса для моделирования распределения .

Далее процедура повторяется с постепенным снижением температуры до некоторого малого значения . В силу предложения 7.3. при малых значениях температуры распределение сосредоточено вблизи глобального минимума и есть шанс получить «почти оптимальное» значение .

В этом алгоритме есть несколько эвристических моментов:

1. не определено количество шагов алгоритма Метрополиса-Хастингса при фиксированной температуре для получения распределения с заданной точностью (хотя в конкретных случаях возможны теоретические оценки)

2. не ясно, как выбирать температурное расписание . В качестве вариантов используются убывающие арифметические и геометрические последовательности.

Теоретический анализ эффективности этого алгоритма весьма сложен. Но в качестве эвристической процедуры метод отжига пользуется популярностью.

Задачи

1. Обоснуйте алгоритм моделирования геометрического

распределения, основанного на формуле (7.1).

2. Придумайте алгоритм моделирования случайной перестановки из элементов (все перестановки должны быть равновероятны).

3. Объясните, как моделировать следующие распределения:

а) равномерное распределение на отрезке

б) распределение Коши с плотностью

в) треугольное распределение с плотностью

.

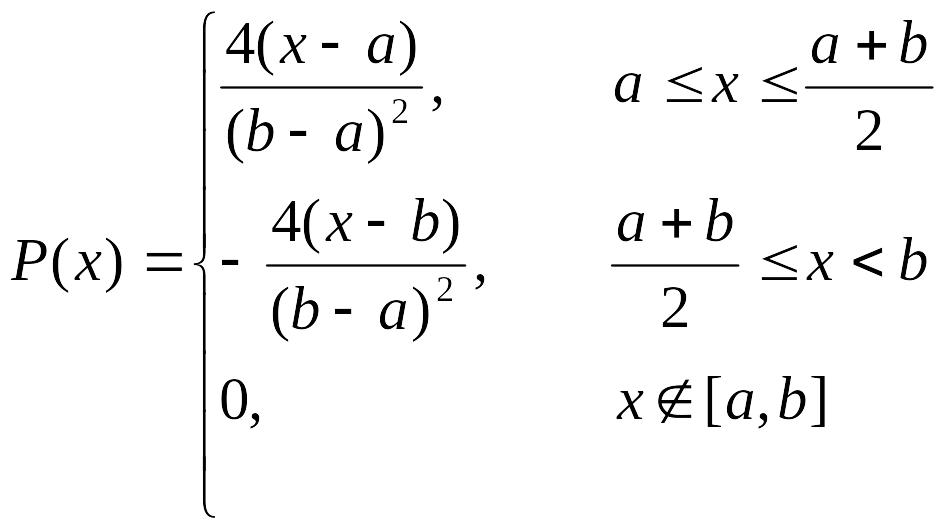4. Дана конечная марковская цепь с матрицей переходных вероятностей за один шаг и начальным распределением . Предложите алгоритм моделирования этой цепи.

5. Предложите алгоритм моделирования нормального распределения с помощью метода отсечений.

6. Докажите формулы (7.9) и проверьте, что величины (7.10) имеют двумерное гауссовское распределение с вектором средних и матрицей ковариаций .

7. Предложите определение окрестности допустимого решения в задаче коммивояжера и запрограммируйте алгоритм отжига для решения этой задачи.