7. Статистическое моделирование

7.1. Моделирование случайных величин

Пусть - некоторая случайная величина с заданным законом распределения. Задача состоит в том, чтобы научиться строить достаточно длинную последовательность чисел, которую можно было бы рассматривать с некоторой точностью как выборку независимых наблюдений над величиной . Существуют различные способы моделирования случайных величин, но мы будем обсуждать только программные генераторы случайных чисел.

Оказывается, что главное в этой науке – это научиться моделировать случайную величину, равномерно распределенную на отрезке . В алгоритмах, которые обсуждаются ниже, каждое новое число в последовательности однозначно определяется предыдущим числом и рано или поздно последовательность зацикливается. Ясно, что последовательности таких чисел не могут рассматриваться теоретически как случайные последовательности и поэтому их называют еще псевдослучайными. В дальнейшем мы для краткости будем называть псевдослучайные числа, моделирующие равномерное распределение на просто случайными числами. Качество последовательности псевдослучайных чисел проверяется с помощью статистических тестов на равномерность и независимость.

Проверку на равномерность можно провести, например, с помощью критерия Колмогорова-Смирнова. Пусть – эмпирическая функция распределения для выборки :

,

где – индикатор луча ,

Функция распределения случайной величины с равномерным распределением равна

Статистика Колмогорова

должна быть мала, если выборка взята из распределения . По теореме Колмогорова

.

Для заданного уровня значимости критерий Колмогорова отвергает гипотезу о равномерности, если , где – соответствующий квантиль функции .

Проверку на независимость можно провести, например, с помощью критерия перестановок. Для данной выборки рассмотрим блоки произвольной длины , и т.д. Если гипотеза о независимости наблюдений верна, то все различных упорядочений должны быть одинаково вероятны, а это можно проверить с помощью критерия .

Проблема построения хороших датчиков случайных чисел до сих пор является актуальной, и в ее истории случались курьезные моменты.

Один из первых датчиков случайных чисел предложен Дж.Нейманом. Интересно отметить, что Дж.Нейман и С.Улам впервые использовали только что появившиеся ЭВМ для статистического моделирования в ходе работы над американским атомным проектом. Метод середины квадратов состоит в том, что берется произвольное четырехзначное число , возводится в квадрат, из которого выделяются четыре средние цифры. Например, обозначим получившееся число . Тогда первое случайное число . Далее процедура применяется к числу и т.д. Ясно, что этот датчик зациклится по крайней мере через 10⁴ шагов.

В настоящее время часто используются так называемые конгруэнтные датчики. Они имеют вид:

,

,

где - натуральные числа, - произвольное натуральное число. Числа образуют последовательность псевдослучайных чисел, . Если , то датчик называется мультипликативным. Популярным примером является датчик с . Неудачным оказался датчик RANDU ( ), вошедший в библиотеку научных программ для IBM-360. Недостатком конгруэнтных датчиков является заметная корреляция между последовательными значениями случайных чисел.

В дальнейшем мы будем считать, что датчики, использующиеся в программном обеспечении современных компьютеров, достаточно хороши и выдерживают проверку статистических критериев на равномерность и независимость при больших объемах выборок.

Обратимся теперь к вопросу моделирования наиболее часто используемых распределений вероятностей.

Дискретная случайная величина (общий случай). Пусть - дискретная случайная величина,

.

Обозначим через случайную величину с равномерным распределением на . Разобьем отрезок на интервалы

.

Зададим случайную величину правилом: , если . Ясно, что . Отсюда получаем алгоритм:

1. Прогенерировать случайное число (пользуясь своим или компьютерным датчиком)

2. Определить номер того интервала , для которого

3. Положить .

При построении выборки для каждого числа нам нужно одно случайное число из выборки для равномерного закона. Этот алгоритм можно эффективно использовать в том случае, когда число значений величины не очень велико. Для моделирования дискретных случайных величин с большим или бесконечным числом значений используются другие алгоритмы.

Геометрическое распределение. Пусть случайная величина имеет геометрическое распределение с параметром , если

.

Рассмотрим последовательность независимых испытаний, в которых «орел» выпадает с вероятностью , а «решка» - с вероятностью . Тогда количество испытаний до первого выпадения «орла» имеет геометрическое распределение. Отсюда следующий алгоритм для моделирования :

1. Генерировать последовательность случайных чисел для распределения и определить номер такой, что

2. Положить .

В этом алгоритме для моделирования одного числа может понадобиться достаточно много случайных чисел .

Другой алгоритм следует из того факта, что случайная величина

(7.1)

имеет геометрическое распределение с параметром . Здесь  , обозначает целую часть числа.

Биномиальное распределение. Пусть случайная величина имеет биномиальное распределение с параметрами и :

.

Вспомним, что биномиальное распределение возникает, когда мы вычисляем вероятность выпадения ровно «орлов» в серии из независимых испытаний, а вероятность выпадения «орла» в одном испытании равна .

Алгоритм:

1. Генерируем случайных чисел из распределения

2. Подсчитываем сумму

,

где - индикатор отрезка

3. Полагаем .

Случай пуассоновского распределения мы обсудим в следующем разделе. Перейдем к непрерывным распределениям вероятностей. Здесь удобно использовать метод обратного преобразования.

Пусть случайная величина имеет функцию распределения .

Предложение 7.1. Определим функцию как

. (7.2)

Тогда, если случайная величина  , то случайная величина имеет функцию распределения .

Доказательство. Из (7.2) следует и

.

Отсюда

и

.

Метод обратного преобразования легко использовать в случае, когда функцию можно определить явно.

Показательное распределение. Пусть имеет показательное распределение с параметром . Ее функция распределения имеет вид:

.

Тогда

и если  , то

(7.3)

имеет искомое распределение. Заметим, что т.к. также имеет распределение , то можно использовать формулу

. (7.4)

Распределение Эрланга. Распределение Эрланга при имеет функцию распределения, для которой трудно вычислить обратную функцию. Вспоминая, что сумма независимых случайных величин  имеет распределение Эрланга и, пользуясь (7.4), получаем необходимый алгоритм:

1. Прогенерировать случайные числа из распределения

2. Положить

.

Такой метод моделирования случайных величин называется методом свертки (плотность распределения Эрланга является сверткой плотностей показательного распределения).

В общем случае, когда трудно вычислить обратную функцию и трудно использовать специфические свойства распределения, можно использовать метод исключения. Пусть случайная величина имеет плотность распределения вероятностей и функцию распределения . Пусть существует плотность распределения вероятностей такая, что для некоторой константы и для всех . Предположим, что мы можем моделировать распределение с плотностью . Алгоритм исключения для моделирования случайной величины с плотностью состоит в следующем:

1. Прогенерировать величину из распределения с плотностью . Предположим

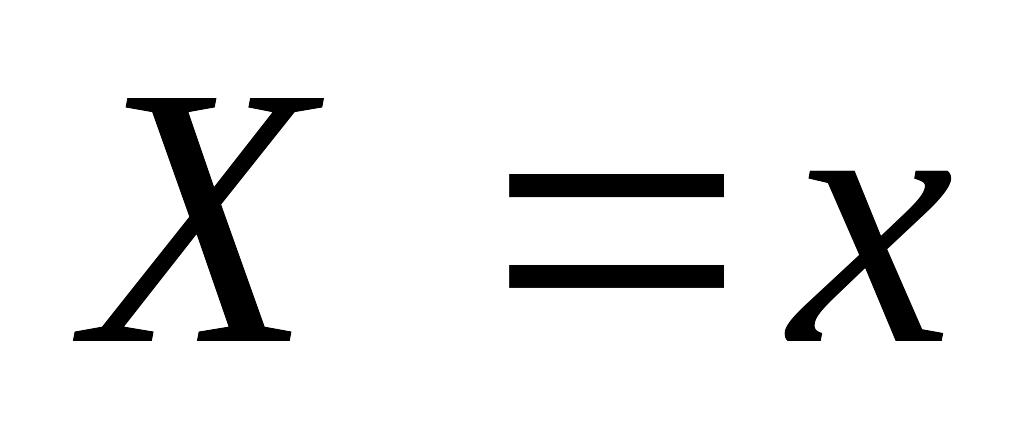
2. Прогенерировать из распределения

3. Принять , если . В противном случае вернуться к шагу 1.

Докажем справедливость этого алгоритма. Пусть обозначает случайную величину с плотностью и – характеристическая функция множества , если , если . Тогда

.

В частности

.

Следовательно,

и величина , при условии, что она принята, действительно имеет плотность .

Рассмотрим в качестве примера плотность

Ясно, что трудно вычислить обратную функцию к функции распределения такой величины. Легко видеть, что

.

Значит плотность мажорируется функцией , где – плотность распределения . Отсюда алгоритм:

Генерируем две величины из распределения и если , то полагаем , в противном случае повторяем процедуру.

Нормальное распределение. Обсудим два способа моделирования нормального распределения. Приближенный метод использует центральную предельную теорему, которая утверждает, что для любой последовательности независимых, одинаково распределенных величин со средним и дисперсией

.

Здесь означает сходимость по распределению, обозначает стандартное нормальное распределение. Пусть  . Тогда . Следовательно, величина приближенно имеет нормальное распределение. В этом алгоритме для получения одного «нормального» случайного числа требуется 12 обычных случайных (равномерных) чисел. Для увеличения точности нужно брать большее количество слагаемых, но тогда нужна дополнительная нормировка. Метод Бокса-Мюллера является точным.

Предложение 7.2. Пусть    независимые случайные величины. Тогда

, (7.5)

(7.6)

являются независимыми величинами,   .

Доказательство. Рассмотрим случайные величины

,

( и можно рассматривать как полярные координаты точки в плоскости ). Выполняя обратное преобразование, получаем

.

Из (7.5), (7.6) следует, что

,

.

Так как и независимы, то и также независимы. При этом ~ , и значить плотность для . Простая выкладка показывает, что плотность случайной величины равна . Значит, совместная плотность

.

Тогда

,

где интегрирование ведется по множеству

.

Переходя к декартовым координатам,

и зная, что , получаем

.

Последняя формула означает, что и независимы, и имеют стандартное нормальное распределение.

Формулы (7.5) и (7.6) и определяют алгоритм Бокса-Мюллера.