6. Марковские процессы принятия решений

6.1. Модели с конечным горизонтом планирования. Задача о замене оборудования

Предположим, что имеется марковская система с конечным множеством состояний . Будем считать, что время дискретно, . Если система находится в состоянии в момент времени , то у нас имеется возможность повлиять на поведение системы с помощью некоторого управления , где – множество всех возможных управлений в состоянии . Выбор управления влияет на вероятности перехода в момент времени :

.

Предположим, что при переходе из состояния в состояние в случае использования управления мы получаем доход . Если в момент времени система оказывается в состоянии , то мы получаем дополнительный доход (финальную плату) . Таким образом, для случайной эволюции , в которой мы использовали управления , суммарный доход записывается как

.

Если нам известно начальное распределение вероятностей состояний системы , то среднее значение дохода за весь период равняется

.

Задача состоит в том, чтобы найти стратегию управления , максимизирующую средний доход за весь период времени. При этом мы будем предполагать, что управление зависит только от времени и текущего состояния .

Эта задача сводится к задаче динамического программирования с конечным числом этапов. Определим как оптимальный средний доход за этапы при условии, что система находилась в состоянии в момент времени . В дальнейшем для большей простоты мы будем предполагать, что множество возможных управлений для всех состояний является одним и тем же: . Мы можем записать обратное рекуррентное соотношение, связывающее функции и :

, (6.1)

. (6.2)

Уравнение (6.1) называют уравнением динамического программирования или уравнением Беллмана. Оно следует из того соображения, что для оптимизации управления на интервале можно сначала оптимизировать управление на интервале , найти функцию , а затем оптимизировать управление на интервале , используя в качестве финальной платы функцию . Решая рекуррентные соотношения (6.1) – (6.2), мы должны запомнить управления

. (6.3)

В результате мы получим стратегию , которая будет максимизировать средний доход за весь период

. (6.4)

Если ввести обозначение для среднего дохода за один этап при переходе из состояния в состояние при управлении

, (6.5)

тогда уравнения (6.1) – (6.2) можно переписать как

, (6.6)

. (6.7)

В качестве примера рассмотрим задачу о замене оборудования. Под состоянием оборудования будем понимать длительность эксплуатации этого оборудования. Пусть множество возможных состояний оборудования равно . В каждом состоянии мы можем использовать два управления: – продолжить использование оборудования, – произвести замену. При управлении система из состояния переходит в состояние с вероятностью , и с вероятностью переходит в состояние 0, если произойдет поломка оборудования (в этом случае старое оборудование придется заменить на новое с нулевым сроком эксплуатации). С увеличением срока эксплуатации вероятность поломки увеличивается и при достижении критического срока она достигает значения 1:

. (6.8)

При управлении система из любого состояния переходит в состояние 0 с вероятностью 1. Таким образом, матрицы переходных вероятностей имеют вид:

.

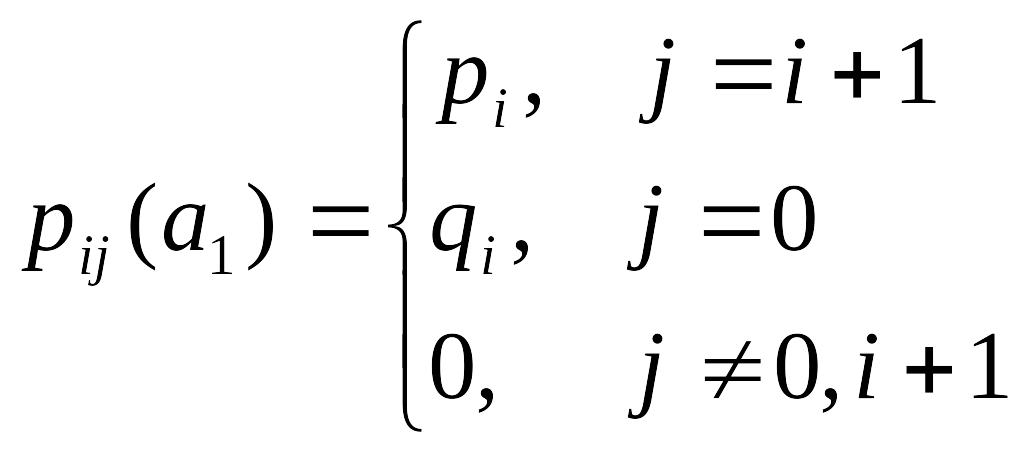
Предположим, что при переходе из состояния в состояние доход , а при переходе в состояние 0 доход . При случайной поломке возможны даже убытки, но мы примем этот уровень доходов за нулевой. При плановой замене оборудования доход от эксплуатации оборудования за соответствующий период равен . Естественно считать, что

. (6.9)

Под финальной платой будем понимать остаточную стоимость оборудования в момент времени ,

. (6.10)

Заметим, что средний доход за один этап равен

,

.

Введем обозначения

, (6.11)

, (6.12)

Тогда уравнения (6.6) – (6.7) примут вид:

, (6.13)

. (6.14)

Обозначим через оптимальное управление (решение), которое следует принять в начале -го периода в случае, когда срок эксплуатации оборудования равняется :

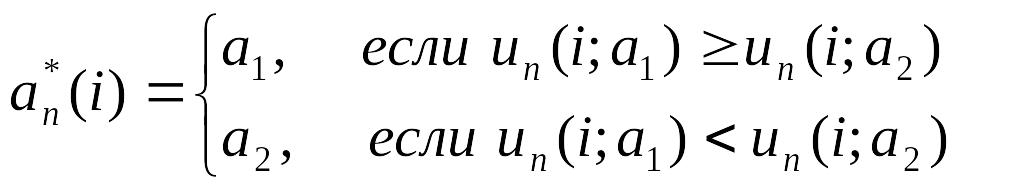. (6.15)

Таким образом, для того, чтобы найти оптимальную стратегию, надо решать рекуррентные соотношения (6.11) – (6.14) и попутно вычислять оптимальные уравнения (6.15).

Явных аналитических формул для величин и не существует, но можно дать качественное описание ответа. Обозначим через множество состояний , в котором оптимальным управлением в момент времени является управления . Кажется правдоподобным, что если в некоторый момент времени выгодно заменить оборудование в возрасте , то тем более выгодно заменить более старое оборудование. Можно доказать, что множество имеет следующую структуру: , . Множество дополнительно к и имеет вид . Используя предположения (6.8) – (6.10), несложно увидеть, что  это наименьшее значение , удовлетворяющее условию

. (6.16)