2. Многоканальная марковская смо с ожиданием. Дисциплины взаимопомощи

Рассмотрим марковскую СМО , в которой имеется каналов обслуживания и мест в очереди.

Под состоянием системы понимается количество заявок в системе. Заявка, приходящая в систему, встает на обслуживание в любой свободный канал, в противном случае встает в очередь. Если же длина очереди достигла максимального значения , заявка уходит из системы. Граф состояний выглядит следующим образом:

1

n

n+1

n+m

0

рис. 5.3

Из анализа, проведенного в разделе 5.1, следует, что

,

,

.

Поскольку мы имеем дело с процессом «размножения и гибели», то, используя (5.6), (5.8), получаем

, (5.34)

, (5.35)

(5.36)

Отсюда следуют следующие выражения для вероятности отказа, относительной и абсолютной пропускных способностей:

, (5.37)

, (5.38)

. (5.39)

Среднее количество заявок в очереди

.

Воспользовавшись формулой (5.19), получаем

, (5.40)

где .

Подсчитаем среднее время ожидания заявки в очереди. Если заявка приходит в систему, в которой есть свободные каналы, то она сразу встанет на обслуживание. Если система находится в состоянии (очередь пустая, все каналы работают), то заявка будет ждать до первого освобождения. Это время равно , где все ~ и независимы между собой. Следовательно, время ожидания заявки в очереди ~ и . Если же заявка приходит в систему, находящуюся в состоянии , она должна пропустить впереди себя заявок, и поэтому среднее время ожидания такой заявки в очереди будет равно . Значит, среднее время ожидания заявки в очереди

. (5.41)

Формула Литтла остается справедливой и в этом случае:

.

В этой СМО появляется такая новая характеристика, как среднее число работающих каналов. Пусть – число работающих каналов. Математическое ожидание этой случайной величины равно

.

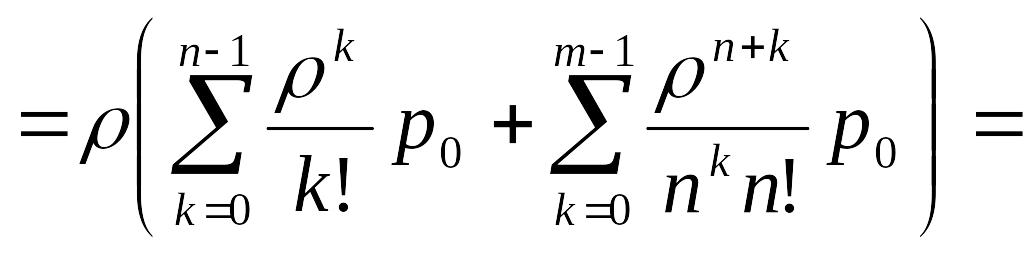
Из этой выкладки следует, что

. (5.42)

Из формул (5.39) и (5.42) следует соотношение

, (5.43)

которое легко интерпретируется и фактически предлагает более легкий способ получения формулы (5.42). Действительно, если один канал за единицу времени может обслужить заявок, а в целом система за единицу времени обслуживает заявок, то среднее число работающих каналов должно равняться .

Среднее число заявок в системе находится из соотношения

. (5.44)

Используя формулы (5.24) и (5.25), получаем, что среднее время пребывания заявки в системе равно

, (5.45)

где – относительная пропускная способность (или вероятность обслуживания).

Приведем ответы для системы с бесконечной очередью. Эти ответы могут быть получены непосредственно или предельным переходом при из ответов для системы . Для того, чтобы предельные вероятности существовали, необходимо потребовать, чтобы . При стационарного состояния не существует и очередь бесконечно возрастает.

Формула (5.36) для изменится на формулу

, (5.46)

а соотношения (5.34), (5.35) останутся теми же.

Очевидно, что в случае бесконечной очереди

. (5.47)

Среднее число заявок в очереди равно

. (5.48)

Среднее время ожидания в очереди

. (5.49)

Среднее число работающих каналов

. (5.50)

Рассмотрим различные варианты «взаимопомощи» между каналами. Если каналы работают «каждый сам за себя», то мы имеем дело с системой , характеристики которой мы только что описали. Предположим теперь, что все каналы объединяются в один, но этот канал способен обслужить за единицу времени в среднем в раз заявок больше, чем обычный канал. Предположим также, что новая система по-прежнему является марковской, т.е. время обслуживания является показательным. Такое предположение ничем не мотивировано, но мы сделали его для того, чтобы остаться в рамках разработанной схемы. Фактически мы приходим к системе , в которой интенсивность канала равна . Такая дисциплина взаимопомощи называется дисциплиной « все как один».

Наконец, предположим, что каналы работают по принципу « равномерной взаимопомощи». Это означает, что в случае, когда в системе находится заявок, , то все каналы разбиваются на группы, и каждая группа обслуживает одну заявку. Если какая-то группа закончила свою работу, то она приходит на помощь другим группам. Опять предположим, что при такой взаимопомощи марковский характер системы не изменится.

Граф состояний системы с равномерной взаимопомощью имеет вид:

0

1

2

n+m

Рис. 5.4

Фактически мы имеем дело с одноканальной системой с интенсивностью канала и максимальной длиной очереди .

Несложно показать, что основные характеристики системы с равномерной взаимопомощью лучше, чем у систем с другими дисциплинами взаимопомощи. Но надо понимать, что анализ этих вопросов в реальных СМО сложнее. Например, предположение о том, что объединение каналов приводит к -кратному увеличению интенсивности разумно только при небольших значениях .