Сложный пуассоновский процесс и процессы риска в страховой математике
Пусть имеется пуассоновский поток заявок, а если заявки характеризуются независимыми случайными величинами (размерами этих заявок). Например, имеется случайный поток покупателей, каждый из которых заказывает какое-то свое количество одного и того же товара. Или имеется поток страховых случаев по определенному виду страхования, и ущерб по каждому иску имеет свое значение.
Мы формализуем такие потоки в виде так называемого сложного пуассоновского процесса.
Пусть
-
последовательность независимых одинаково
распределенных случайных величин,
.
Величины
задают размеры заказов или исков. Для
упрощения мы предположим, что величины
являются целочисленными. Пусть
- пуассоновский случайный процесс
интенсивности
,
независимый от случайных величин
.
Рассмотрим случайный процесс
,
который мы будем называть сложным пуассоновским процессом.
Теорема.
Математическое
ожидание и дисперсия процесса
равны
.
Доказательство.
Трудность состоит в том, что мы имеем
случайное количество случайных слагаемых.
Воспользуемся формулой полной вероятности.
События
образуют полную группу событий.
.
Для вычисления
дисперсии вычислим сначала
:
.
Отсюда
.
Так как
,
то мы получаем утверждение теоремы.
Можно показать,
что для случайной величины
при
справедлив аналог центральной предельной
теоремы:
.
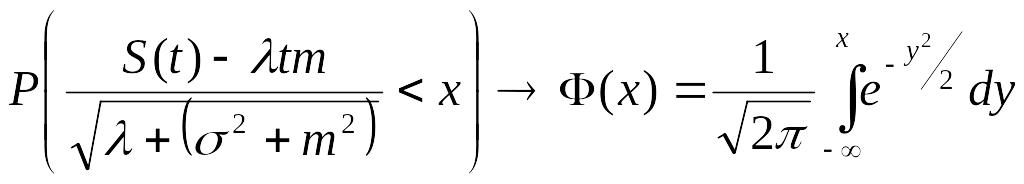Это означает, что распределение центрированной случайной величины при больших значениях или можно считать приближенно гауссовским.
Если интерпретировать величины как размеры выплат по страховым случаям, а - количество наступивших страховых случаев за время , то процесс означает суммарную выплату и в страховой математике называется процессом риска.
Пусть страховая
компания имеет в начале года капитал
,
и в единицу времени собирает
рублей страховых сборов. Предположим
для простоты, что все выплаты по всем
страховым случаям в интервале
будут производиться в конце периода,
т.е. в момент времени
.
Какова должна быть интенсивность
страховых сборов
,
чтобы с заданной вероятностью
компания была способна произвести все
выплаты?
.
Пусть
-
-квантиль
нормального распределения,
.
Тогда
.
Задачи
1. Случайный поток
заявок является пуассоновским потоком
с интенсивностью
заявки в час. Какова вероятность того,
что между 10 и11 часами придет а) 0 заявок,
б) более 3 заявок? Предположим, что первые
две заявки пришли в течение часа (с10 до
11). Какова вероятность того, что обе
заявки пришли в течение первых 30 минут?
2. Пусть
и
являются независимыми пуассоновскими
процессами с интенсивностью
и
соответственно. Докажите, что суммарный
поток
является пуассоновским потоком с
интенсивностью
.
3. Пусть
является пуассоновским потоком заявок
с интенсивностью
.
Каждая заявка независимо от других с
вероятностью
является заявкой 1-го типа и с вероятностью
– заявкой 2-го типа. Докажите, что заявки
только 1-го и только 2-го типов образуют
независимые пуассоновские потоки с
интенсивностью
и
соответственно.
4. Докажите, что плотность распределения Эрланга имеет вид (4.8).
5. Фабрика шьет модные рубашки на летний сезон. Известно, что половина покупателей берет одну рубашку, треть – две и оставшаяся часть – три рубашки. Число покупателей в сезон имеет пуассоновское распределение с интенсивностью 10000 человек за сезон. Себестоимость одной рубашки – 100 рублей, а цена – 300 рублей. Оцените, какое число рубашек следует пошить, чтобы средний доход был максимален.