2. Пуассоновский поток как марковский процесс. Немарковские потоки

Рассмотрим марковскую цепь с непрерывным временем, в которой множеством состояний является , а вероятности перехода за малое время удовлетворяют следующим условиям:

(4.5)

, если .

Мы интерпретируем эту марковскую цепь как случайный поток событий, где состояние цепи в момент времени определяется как количество событий, происшедших в интервале . Понятно, что при увеличении времени число событий только увеличивается, и переход из состояния с большим номером в состояние с меньшим номером невозможен. Запишем уравнения Колмогорова для вероятностей . В данном случае плотность выхода из состояния равна , при . Уравнения (3.25) будут выглядеть так:

, (4.6)

.

Начальные условия имеют вид

.

Введем функции . Уравнения (4.6) перепишутся следующим образом:

,

,

с начальными условиями при . Используя математическую индукцию, легко доказать, что решения этой бесконечной системы уравнений имеют вид

.

Отсюда

и значит, величина имеет пуассоновское распределение с параметром .

Этот марковский процесс можно охарактеризовать еще следующим образом. Пусть - случайные моменты поступления требований при . Предположим, что в каждый момент поступает только одно требование. Тогда последовательность таких величин называется точечным случайным процессом. Обозначим - промежуток времени между поступлением -го и -го требования. Случайный точечный процесс , для которого случайные величины образуют последовательность независимых одинаково-распределенных случайных величин, называется простым процессом восстановления. Величина называется -ым моментом восстановления. Такие процессы возникают в задачах теории массового обслуживания и теории надежности. Название объясняется следующей задачей. Пусть некоторый элемент технической системы, отработав случайное время , выходит из строя. Он мгновенно меняется на другой однотипный элемент, который обслужив случайное время , также выходит из строя и т.д. Тогда момент времени называется моментом -го восстановления.

Для марковской цепи, задающий пуассоновский процесс, время пребывания в состоянии имеет показательное распределение с параметром . Значит, пуассоновский процесс можно определить как простой процесс восстановления, для которого функция распределения величин равна

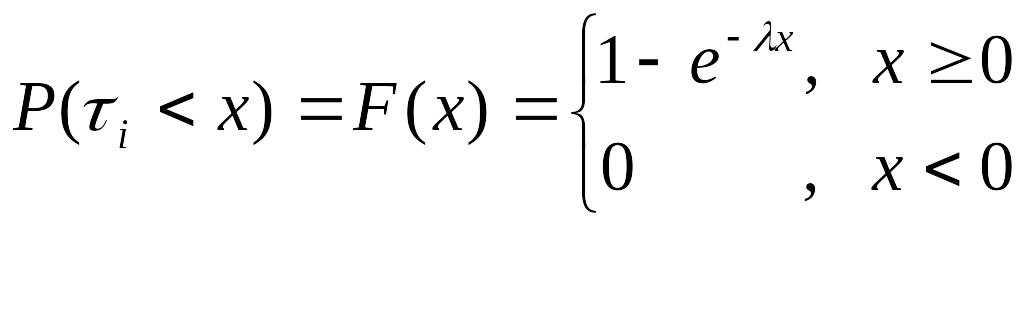
Для произвольного простого процесса восстановления обозначим через количество требований, поступивших в интервале . Очевидно, что

.

Интенсивностью процесса восстановления называется величина

.

Справедлива так называемая элементарная теорема восстановления:

с вероятностью 1 и

. ( 4.7 )

Для пуассоновского процесса

,

и поскольку , предельное равенство (4.7) превращается просто в равенство.

Момент прихода -ого требования для пуассоновского процесса

имеет распределение Эрланга (частный случай гамма-распределения ). Плотность распределения Эрланга имеет вид

, ( 4.8)

.

Если величины не имеют показательного распределения, то процесс восстановления не будет марковским. Понятно, что процесс восстановления можно интерпретировать как случайный поток требований (или событий). Если случайные величины , то такой поток называется детерминированным и при кодировке систем массового обслуживания он обозначается буквой . Пуассоновский поток обозначается буквой ( в силу марковского свойства).

Если времена между поступлениями заявок имеет распределение , то соответствующий случайный поток называется потоком Эрланга порядка и обозначается . Чтобы получить такой поток, надо «прореживать» пуассоновский поток и оставлять из него каждое -е требование. Для потока Эрланга

, .

Обозначим интенсивность потока буквой :

.

Предположим, что интенсивность зафиксирована и равна некоторой константе: . Тогда

.

Мы видим, что математическое ожидание времени между поступлениями заявок постоянно, а дисперсия стремится к 0 при . Другими словами, поток Эрланга «сходится» к детерминированному потоку при , а при он совпадает с пуассоновским потоком . Потоки Эрланга заполняют широкий спектр потоков от простейшего случайного (пуассоновского) потока до детерминированного и поэтому их удобно использовать при моделировании систем массового обслуживания.