Тема 16. Основы теории вероятностей
Пискунов, гл. XX, упр.1-12,14-27, 30-32, 34-38. Разберите решения задач 38—44 из данного пособия.
Задача 38. Всхожесть семян данного растения составляет 90 %. Найти вероятность того, что из пяти посеянных семян взойдут: а) четыре; б) не менее четырех.
Решение: Воспользуемся формулой Бернулли. Если производится п независимых испытаний, при каждом из которых вероятность осуществления событий А постоянна и равна р, а вероятность противоположного события q=1-р, то вероятность Рп(т) того, что при этом событие А осуществляется ровно m раз, вычисляется по формуле:
, (1)
– есть
число сочетаний из п
элементов
по т.
а) По условию задачи вероятность всхожести семян р=0,9; тогда q= 0,1; в данном случае n=5 и т = 4. Подставляя эти данные в формулу Бернулли (1), получим
.
б)
Искомое событие А
состоит
в том, что из пяти посеянных
семян взойдут или четыре, или пять. Таким
образом,
Первое
слагаемое уже найдено.
Для вычисления второго снова применяем
формулу
(1):
.
Следовательно, Р(А) =0,328 +0,591 = 0,919.
Задача 39. Вероятность появления события А в каждом из 625 испытаний равна 0,64. Найти вероятность того, что событие А в этих испытаниях появится ровно 415 раз.
Решение: Если число испытаний п велико, то применение формулы Бернулли приводит к громоздким вычислениям. Использование этой формулы становится практически невозможным. В таких случаях применяют приближенную формулу, которая выражает суть локальной теоремы Лапласа.
Если
вероятность наступления события А
в
каждом из
независимых
испытаний постоянна и равна р
(р отлично
от нуля и единицы), а число п
достаточно
велико, то вероятность Рп(т)
того,
что в этих испытаниях событие
А
наступит
т
раз
(безразлично, в какой последовательности)
вычисляется приближенно по формуле
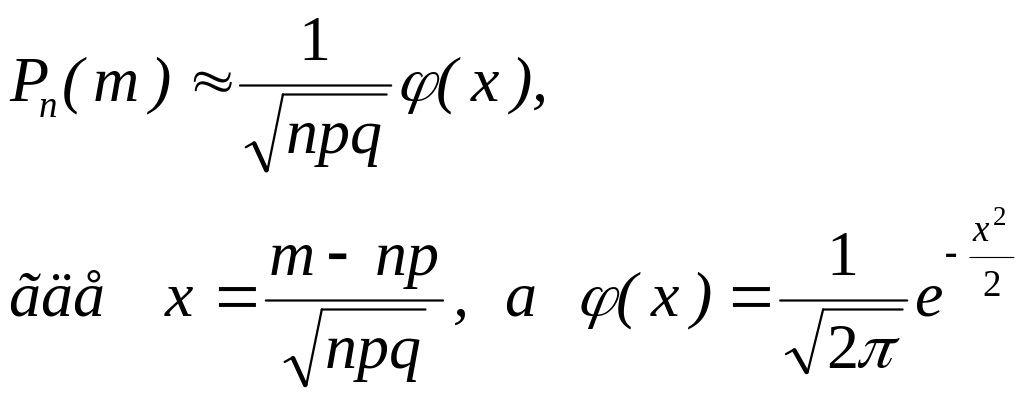(2)
Имеются
готовые таблицы значений функции
(см.
табл. 1 Приложения). Для
х>5
считают,
что
Так как функция φ(х)–четная, то φ(-х)=φ(х). По условию задачи n=625, m=415, р=0,64. Находим q=1–0,64=0,36. Определяем значение x:
По таблице 1 находим, что φ(1,25)=0,1826. Подставив это значение в (2), получим
Задача 40. Среди семян ржи 0,04 % сорняков. Какова вероятность при случайном отборе 5000 семян обнаружить 5 семян сорняков?
Решение: Применение асимптотической формулы (2) для случая, когда вероятность р близка к нулю, приводит к значительному отклонению от точного значения Рп(т). При малых значениях р (и при малых значениях q) применяют асимптотическую формулу Пуассона.
Если вероятность появления события А в каждом из n независимых испытаний мала, а число испытаний п достаточно велико, то вероятность того, что событие А наступит ровно m раз, вычисляется приближенно по формуле
(3)
Формулу
(3) применяют в тех случаях, когда
При этом чем больше число п и меньше число р, тем точнее результат по этой формуле. По условию задачи n = 5000, m = 5, р = 0,0004. Тогда λ = 5000·0,0004 = 2. Применяя (3), получим
Задача 41. Вероятность попадания в цель при отдельном выстреле равна 0,6. Найти вероятность того, что число попаданий при 600 выстрелах будет заключено в пределах от 330 до 375.
Решение:
Формулы Бернулли, Пуассона, асимптотическая
формула (2), выражающая суть локальной
теоремы
Лапласа, позволяют найти вероятность
появления
события А
ровно
m
раз
при п
независимых
испытаниях.
На практике часто требуется определить
вероятность
того, что событие А
наступит
не менее т1
раз
и не более
т2
раз,
т. е. число т
определено
неравенствами
В
таких случаях применяют интегральную
теорему Лапласа.
Если вероятность наступления события А в каждом из п независимых испытаний постоянна и равна р (р отлична от нуля и единицы), а число п достаточно велико, то вероятность того, что событие А в таких испытаниях наступит не менее т1 раз и не более т2 раз, вычисляется приближенно по формуле
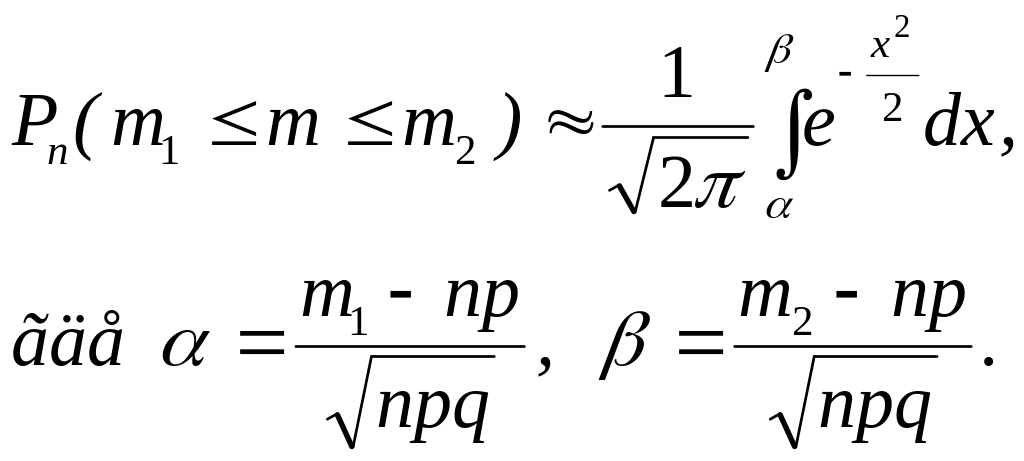(4)
Функция Ф(х) являйся монотонно возрастающей. При неограниченном возрастании х функция Ф(х) стремится к 0,5. Если воспользоваться готовыми значениями функции Лапласа, то формулу (4) можно записать так:
(5)
Имеются таблицы
значений функции
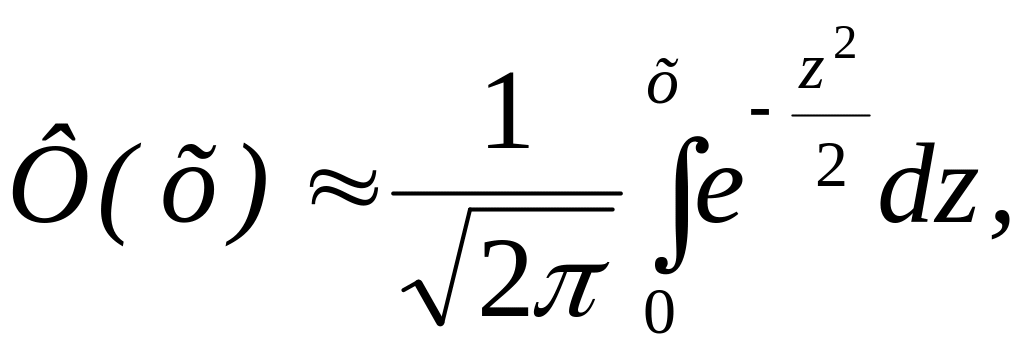(см. табл.
2 Приложения). Функция Φ(х) называется
функцией Лапласа. Эта функция является
нечетной, т.е.
Ф(–х)=–Ф(х).
Поэтому таблица значений дается только
для положительных чисел. По условию n
= 600, p=0,6,
m1=
330, m2=375.
Находим
По таб. 2 находим Ф( 1,25) = 0,3944; Ф(–2,5) = –Ф(2,5)= = – 0,4938. Подставив эти значения в (5), получим искомую вероятность:
Задача 42. Задан закон распределения случайной величины X (в первой строке таблицы даны возможные значения величины X, а во второй строке указаны вероятности р этих возможных значений).
X |
13 |
15 |
18 |
20 |
P |
0.2 |
0.1 |
0.4 |
0.3 |
Найти: 1) математическое
ожидание
;
2)
;
3) среднее квадратическое отклонение
.
Решение: 1)
Математическое ожидание
вычислим по формуле:
.
Тогда имеем:
2) Для вычисления дисперсии воспользуемся формулой:
.
Сначала вычислим
:
.
Тогда получим:
3) Среднее
квадратическое отклонение
:
.
Т.е.
.
Задача 43. Случайная величина X распределена по нормальному закону. Математическое ожидание М(Х) =5; дисперсия D(X) = 0,64. Найти вероятность того, что в результате испытания X примет значение в интервале (4,7).
Решение: Если случайная величина X задана дифференциальной функцией f(x), то вероятность того, что X примет значение, принадлежащее интервалу (α,β), вычисляется по формуле
Если величина X распределена по нормальному закону, то
(6)
где
а=М(Х)
и
.
По
условию задачи а
=
5,
,
α=4
и β=7.
Подставив эти данные в (6), получим:
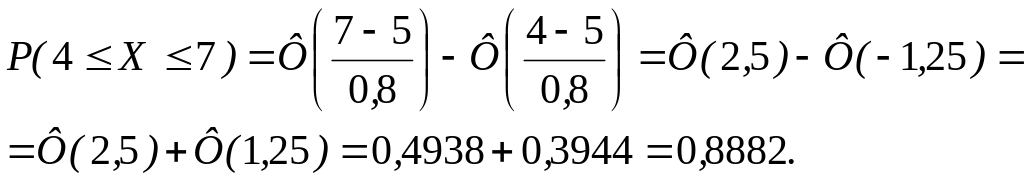
Задача 44. Считается, что отклонение длины изготавливаемых деталей от стандарта является случайной величиной, распределенной по нормальному закону. Стандартная длина (математическое ожидание) а = 40 см, среднее квадратическое отклонение σ = 0,4 см. Найти вероятность того, что отклонение длины от стандартной составит по абсолютной величине не более 0,6 см.
Решение: Если X — длина детали, то по условию задачи эта величина должна быть в интервале (а–δ, а+δ), где а = 40 и δ = 0,6. Подставив в формулу (6) α=а – δ и β= а + δ, получим
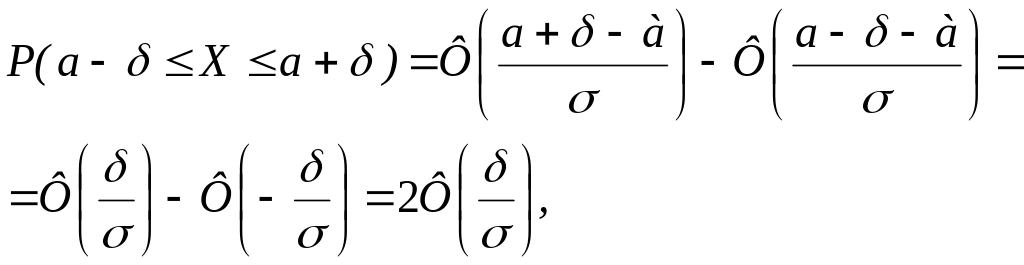
(7)
Таким образом, подставляя в (7) имеющиеся данные, получим
Итак, вероятность того, что изготавливаемые детали по длине будут в пределах от 39,4 до 40,6 см, составляет 0,8864.