2. Випадок кратних коренів

Якщо дійсний корінь х.р. повторюється разів , то відповідні йому ч.р-ки л.о.д.р. будуть такі :

, ,..., .

Якщо пара комплексних коренів х.р. повторюється m разів , то відповідні йому ч.р-ки л.о.д.р. будуть такі :

, , , ,...,

, .

Приклади:

1) ; (3.3.7)

, , .

, .

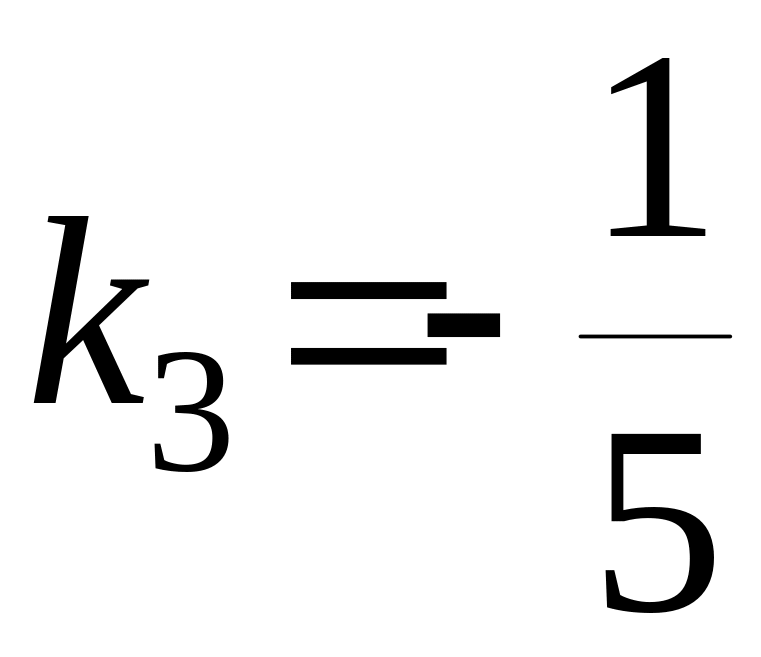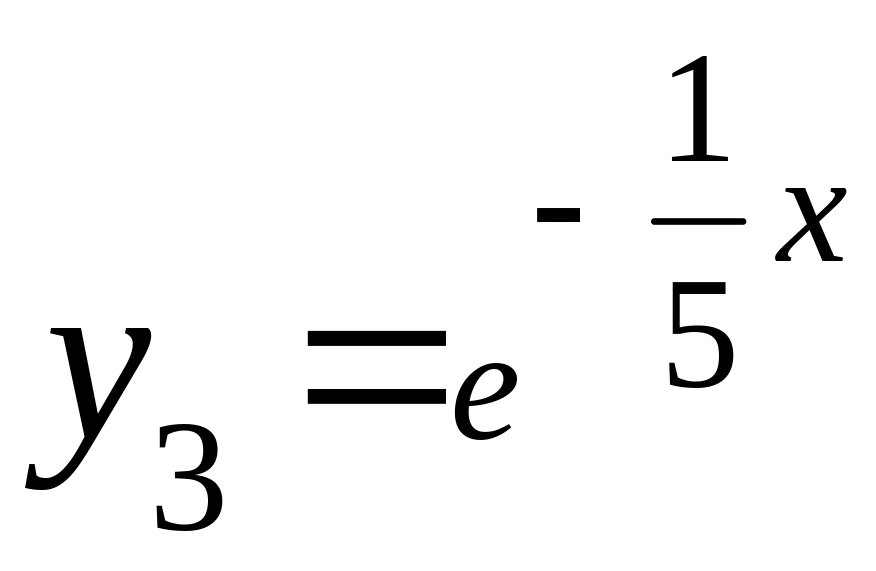З.р-к л.о.д.р. (3.3.7) такий : .

2) + +256=0 ; (3.3.8)

=0 , .

, .

Відповідь: .

3.4Лінійні неоднорідні рівняння зі сталими коефіцієнтами

Загальний розвязок л.н.д.р.

(3.4.1 )

шукаємо , спираючись на попередньо знайдені р-ки відповідного л.о.д.р.

, (3.4.2 )

або методом варіації сталих , або способом підбору ч.р-ку л.н.д.р. y*.

Якщо для л.н.д.р. , в якому коефіцієнти є функціями від х , знаходження y* являється

задачою випадкового підбору , то для лн.д.р. зі сталими коефіцієнтами існує кілька видів , для яких y* знайти завжди можливо.Розглянемо ці випадки.

1. Якщо = 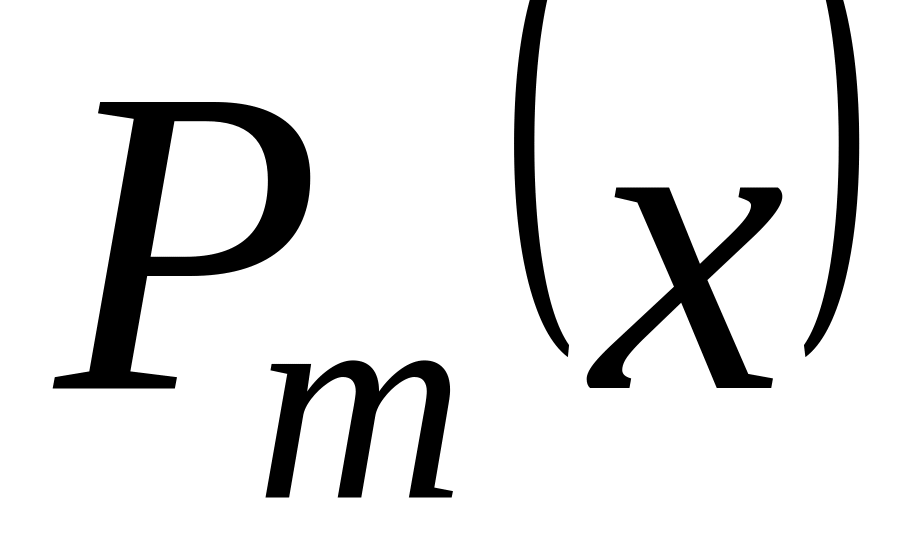, де є многочленом степеня m від х , а серед розв’язків характеристичного рівняння присутній 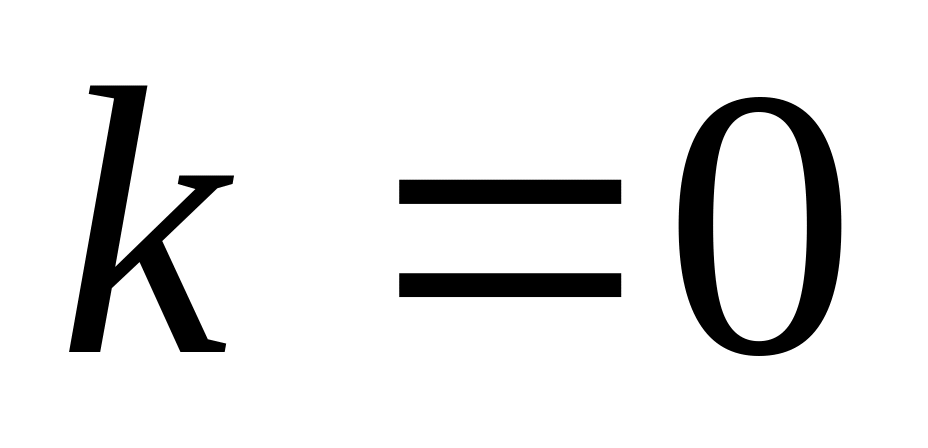кратності r , то шукаємо

, ( 3.4.3)

де є многочлен того ж степеня , що і .

Наприклад

, (3.4.4)

тут х.р. таке :

, ,

.

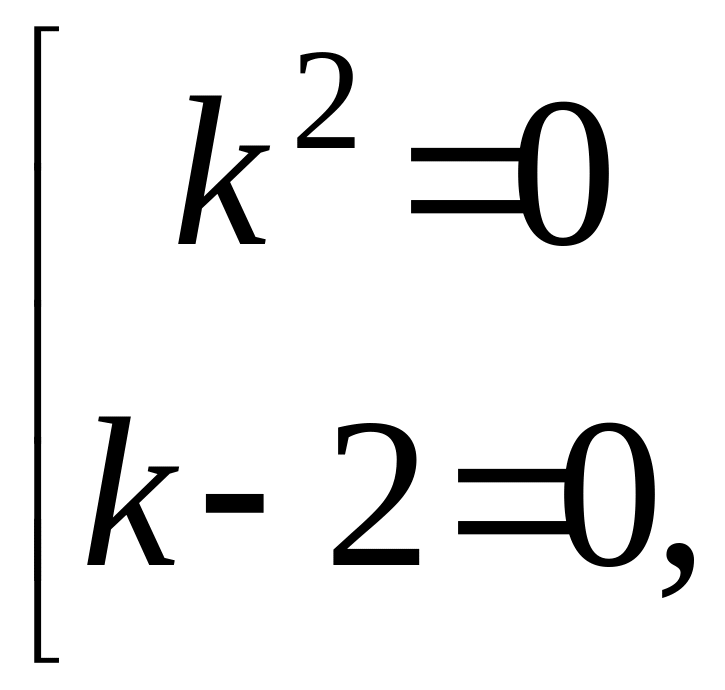
Загальний р-к л.о.д.р. такий :

= , = .

Маємо корінь кратності 2 , отже в (3.4.3) беремо = , (бо в (3.4.4)

є многочлен першого степеня). (3.4.3) прийме вид :

= .

, ,

Підставимо все отримане до (3.4.4).

.

Ця рівність повинна бути справедливою при всіх значеннях ,

а для цього необхідно , щоб були рівними коефіцієнти

при однакових степенях в лівій та правій частинах ріності.

Маємо систему лінійних алгебраїчних рівнянь відносно невідомих А та В.

, ,

.

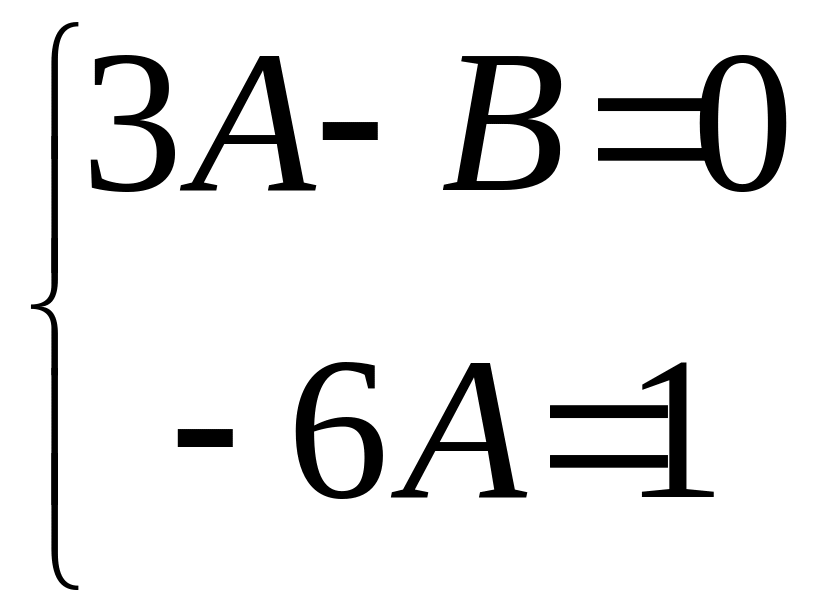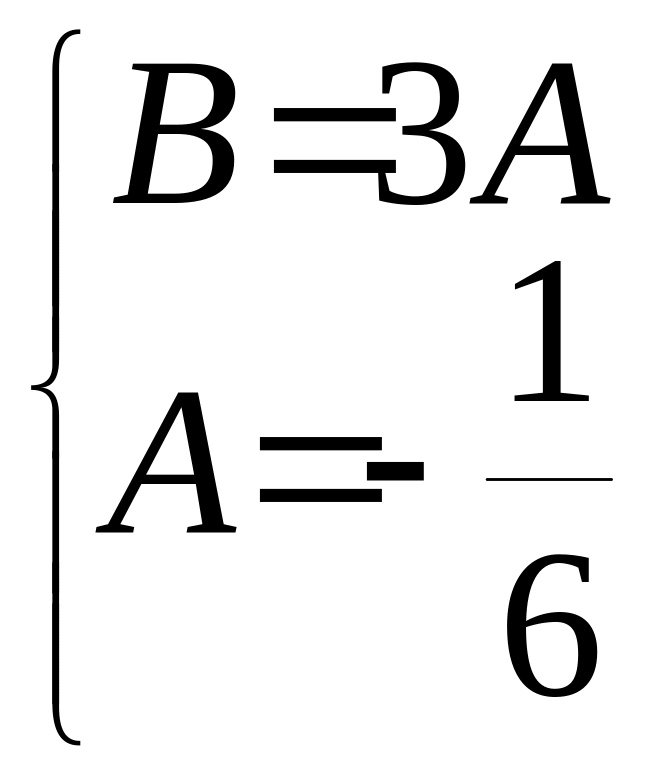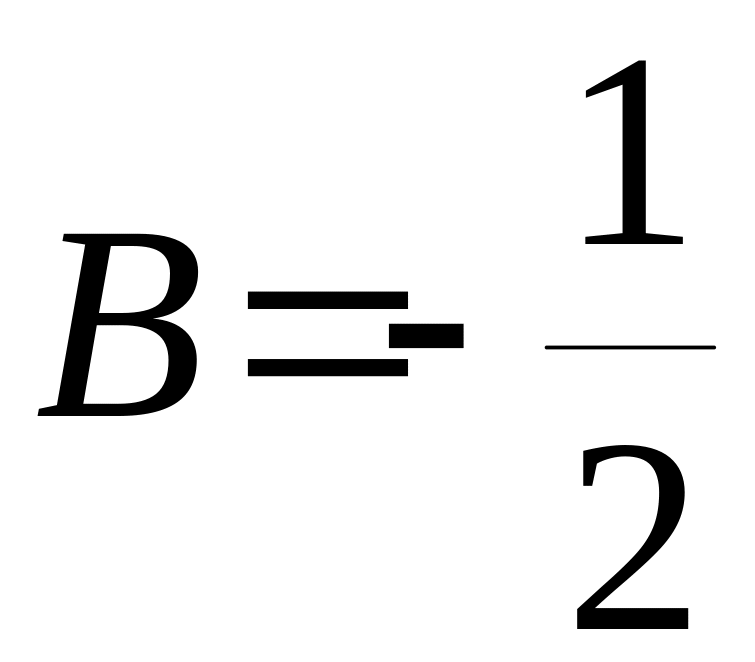
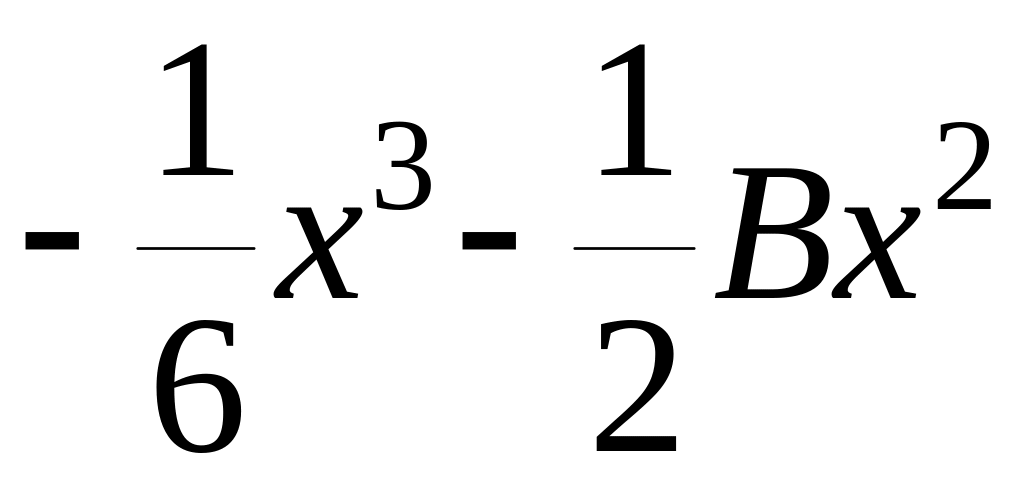З.р-к л.н.д.р. такий : .

Відповідь: = .

2. Якщо = 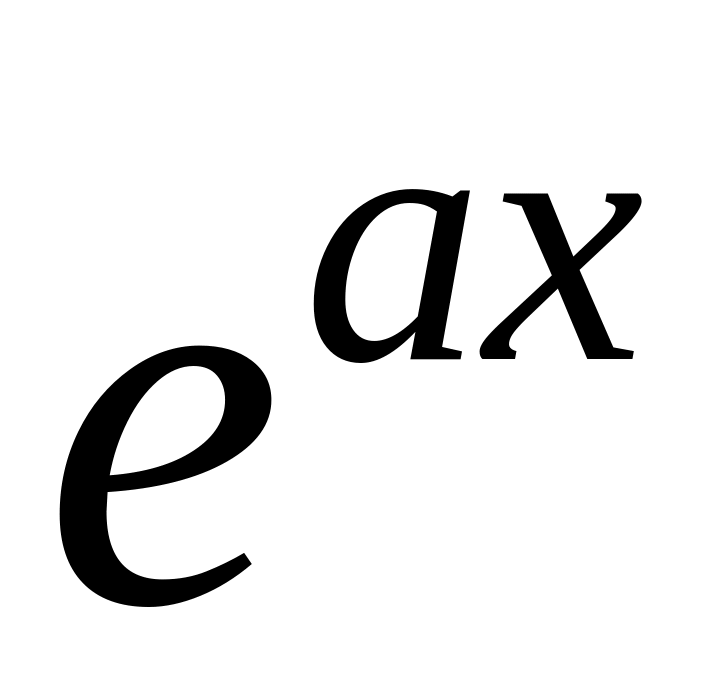, де є многочленом степеня m від х , а серед розв’язків характеристичного рівняння присутній 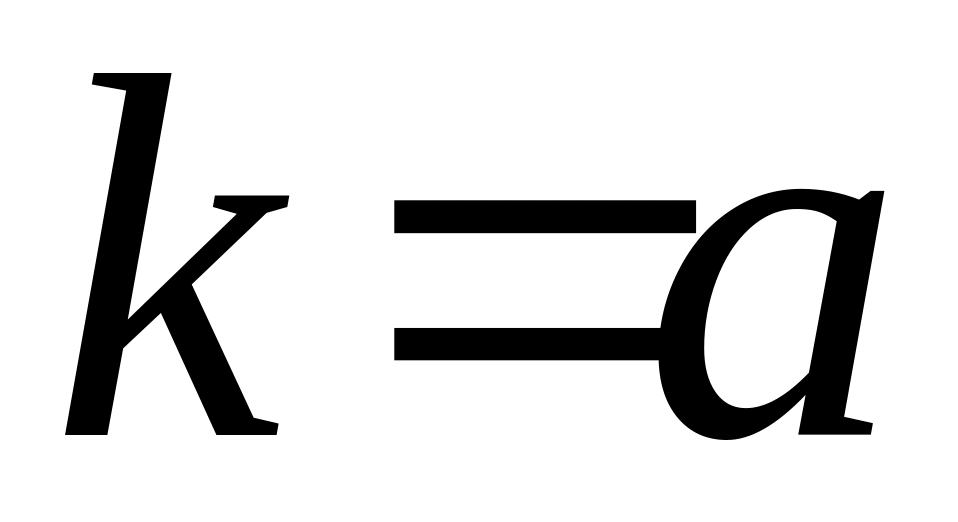кратності r , то шукаємо

, (3.4.3)

де є многочлен того ж степеня , що і .

В подальшому зосередимо свою увагу тільки на л.н.д.р. другого порядку:

, (3.4.4)

де та q є сталі. Відповідне л.о.д.р.

, х.р. таке : . (3.4.5)

Можливі три випадки

1. корені х.р. дійсні , різні , тоді 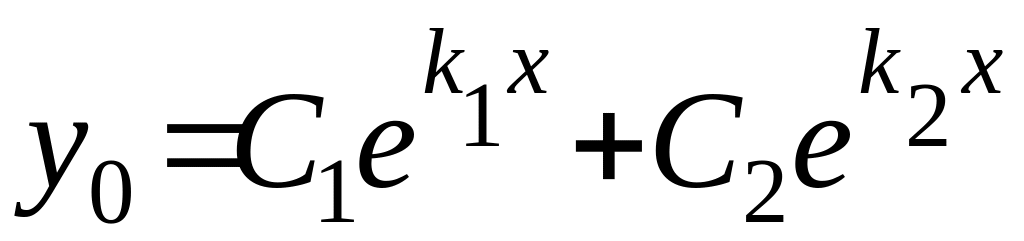, і розглянемо варіанти. Якщо

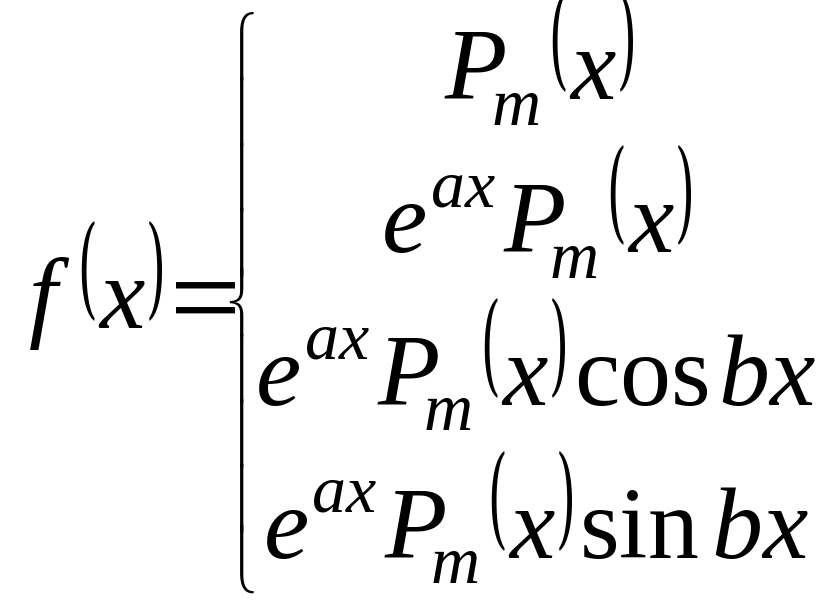
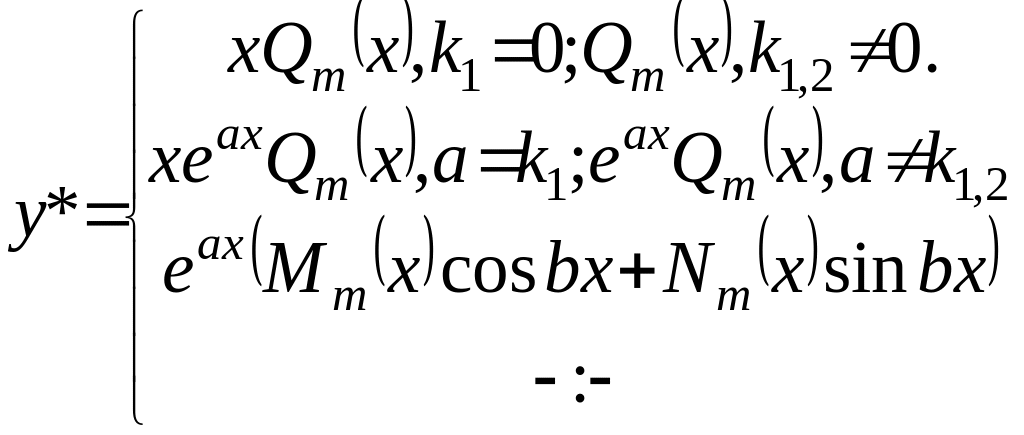
2. корені х.р. дійсні, рівні, тод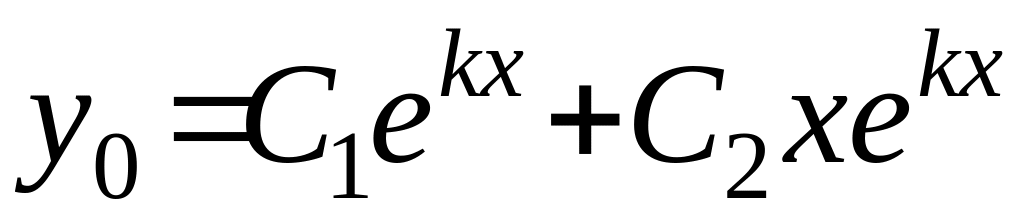і , і

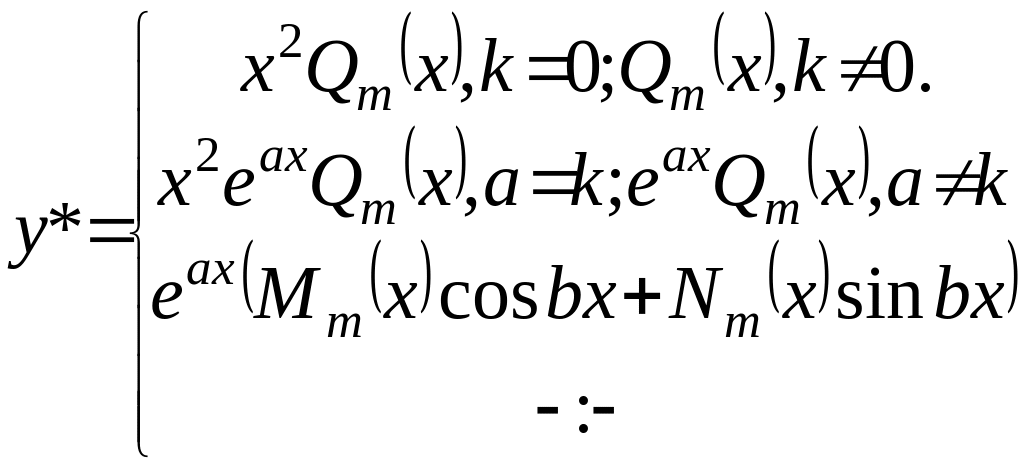
3) корені х.р. комплексні: тоді , і

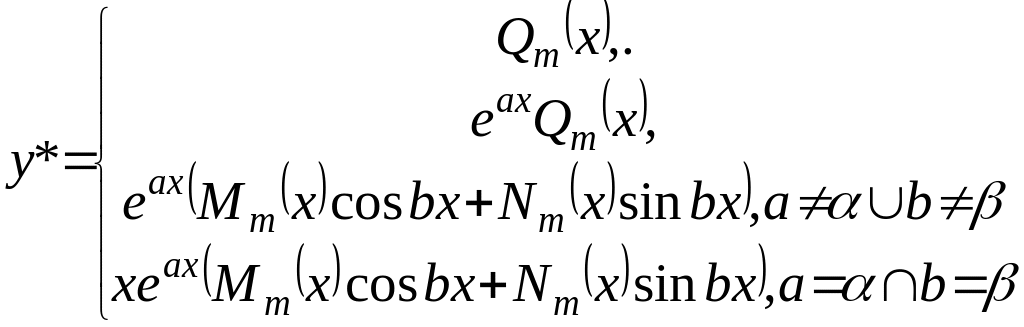
Приклади:

1а) ; (3.4.6)

; ;

; Підставляємо в (3.4.6) та прирівнюємо коефіцієнти при однакових степенях x в лівій та правій частинах рівняння :

; ;

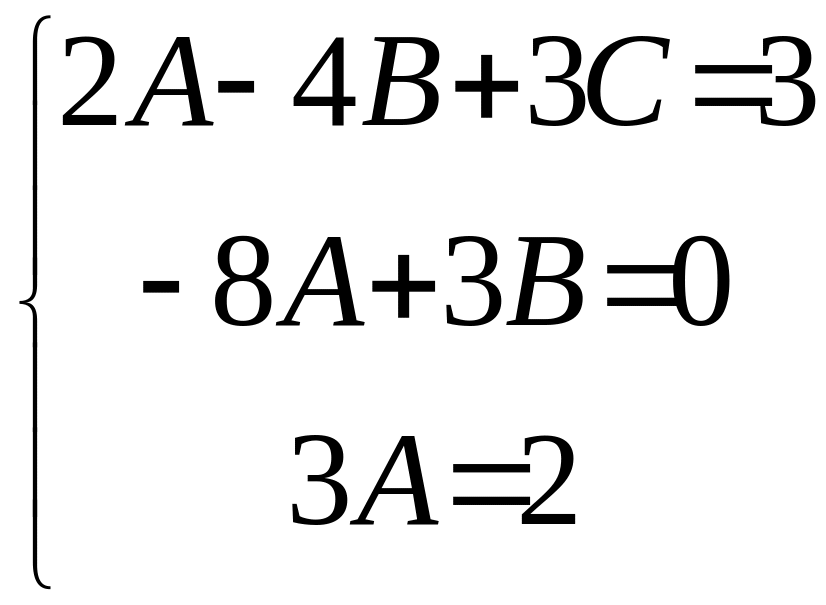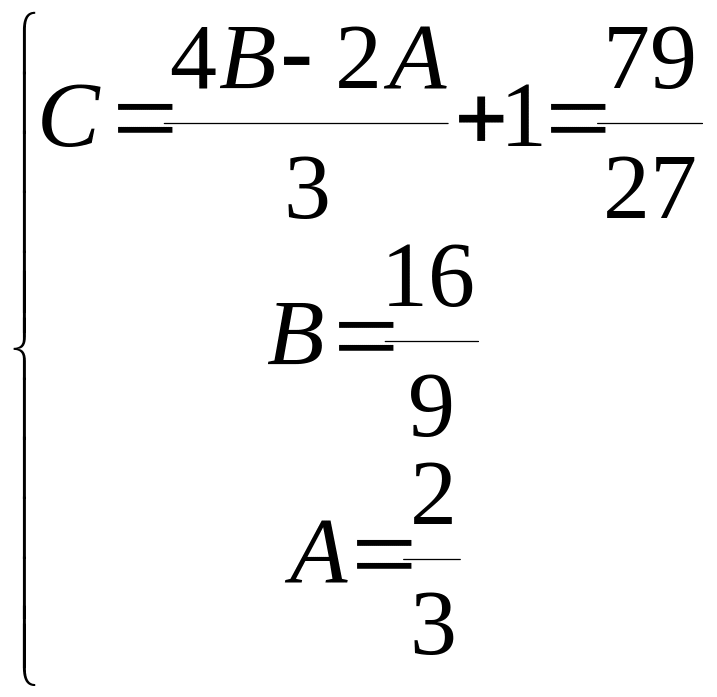Відповідь: y=

1б)

;

y*= ; .

9A +3A -2 = ; 10A=1 ; A= 0,1; y*=0,1 .

Відповідь: y= .

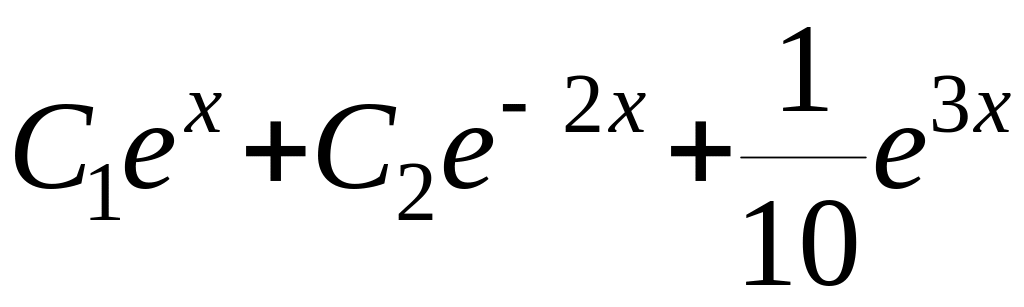1в)

;

; ; = ;

; 3A=-1 ; ; .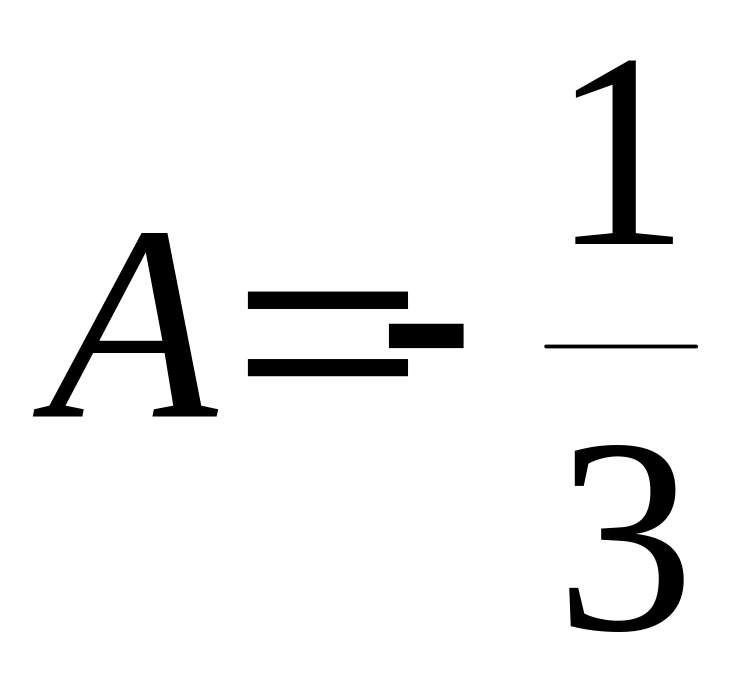

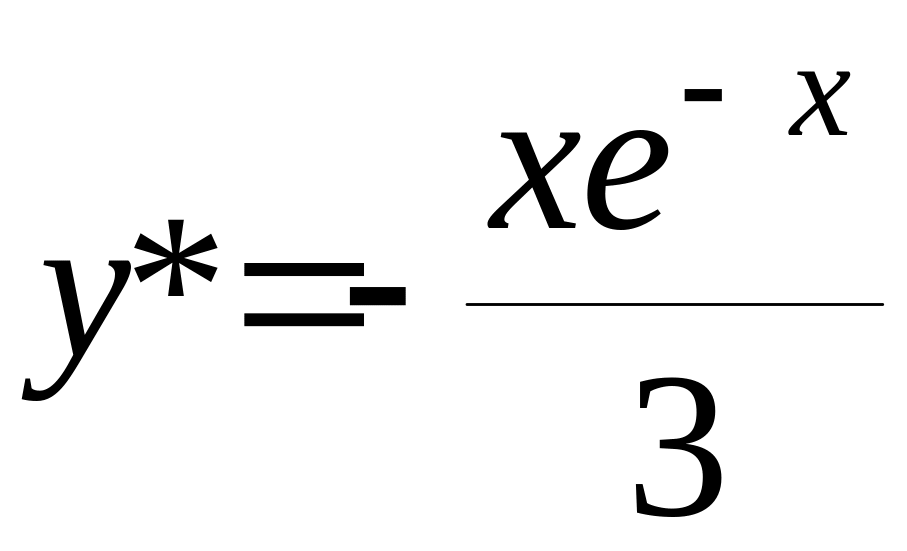Відповідь: .

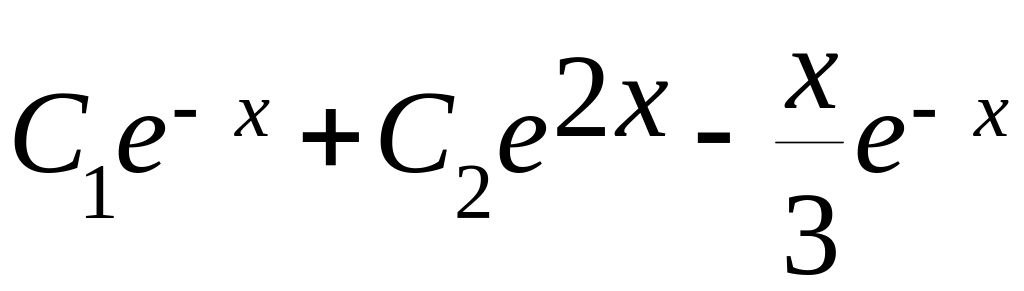1г)

; ;

; .

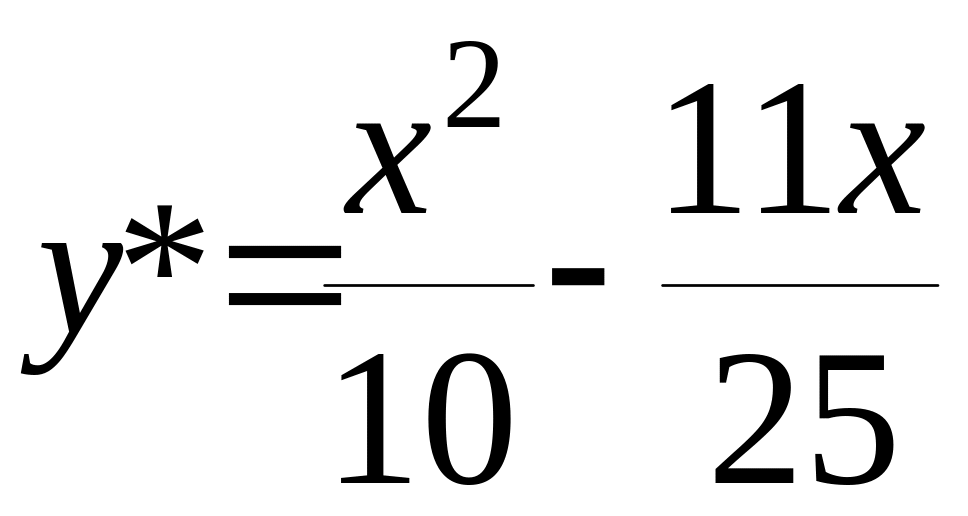Відповідь: .

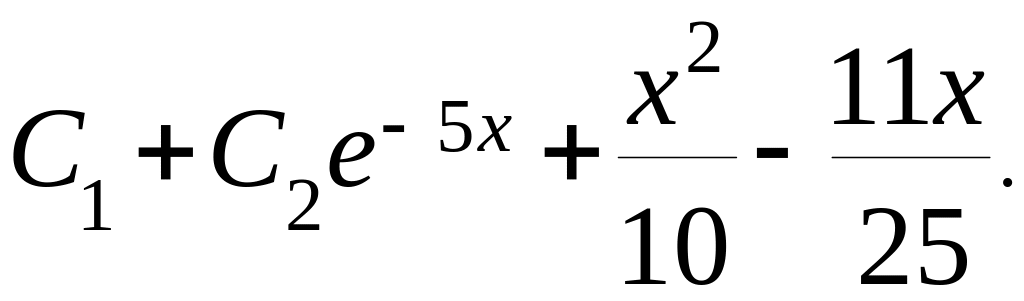1д)

; ;

y*= ; ;

;

Підставляємо y*, та до 1д) і прирівнюємо множники при та в лівій і правій частинах рівняння:

= .

; ; .

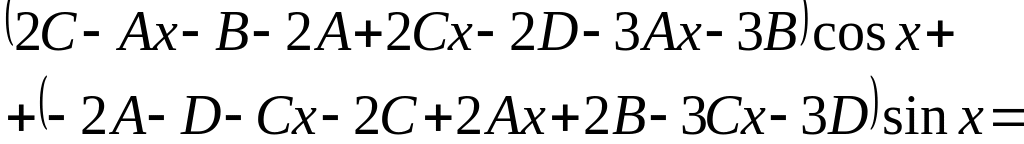
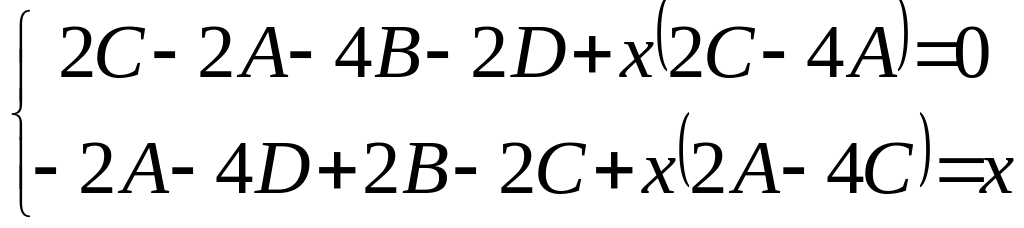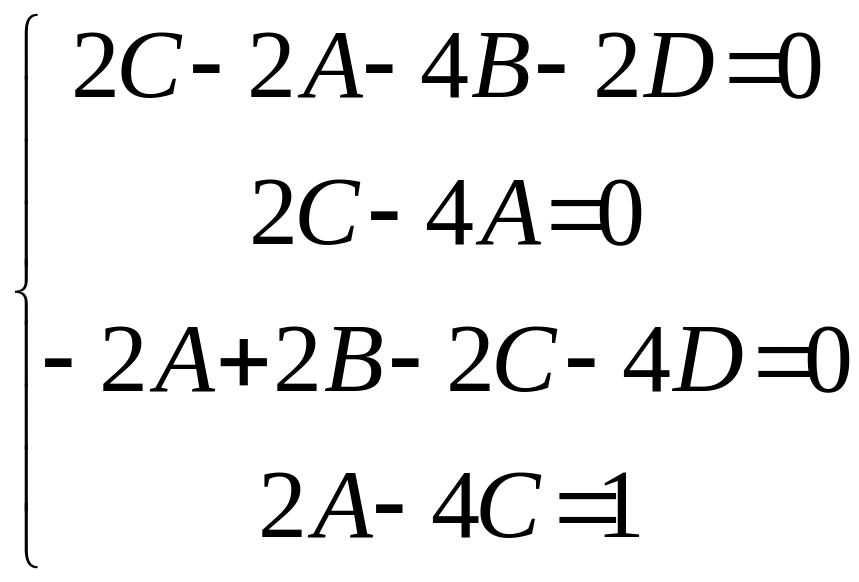
Відповідь: .

1є)

; ,отже = ;

= ;

= ;

Скорочуємо на та прирівнюємо множники при однакових степенях х в лівій і правій частинах рівняння:

; ; ; .

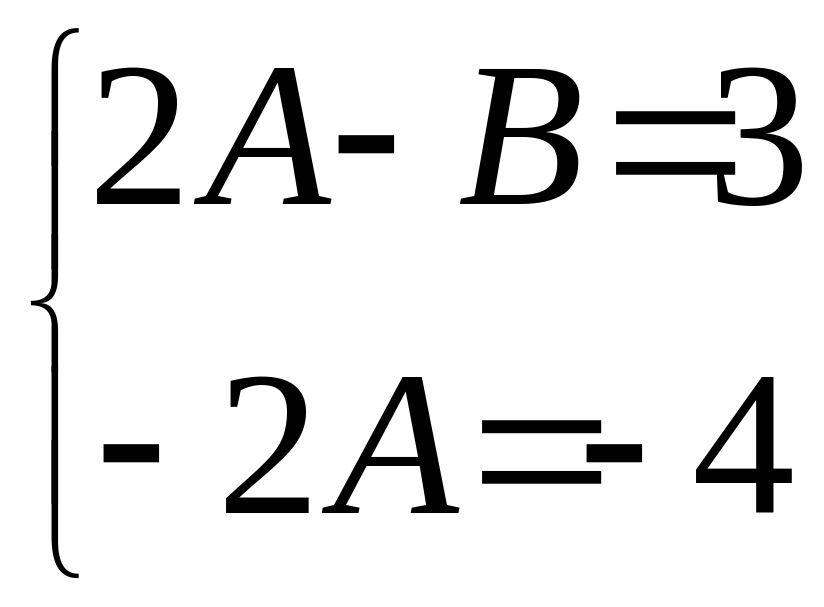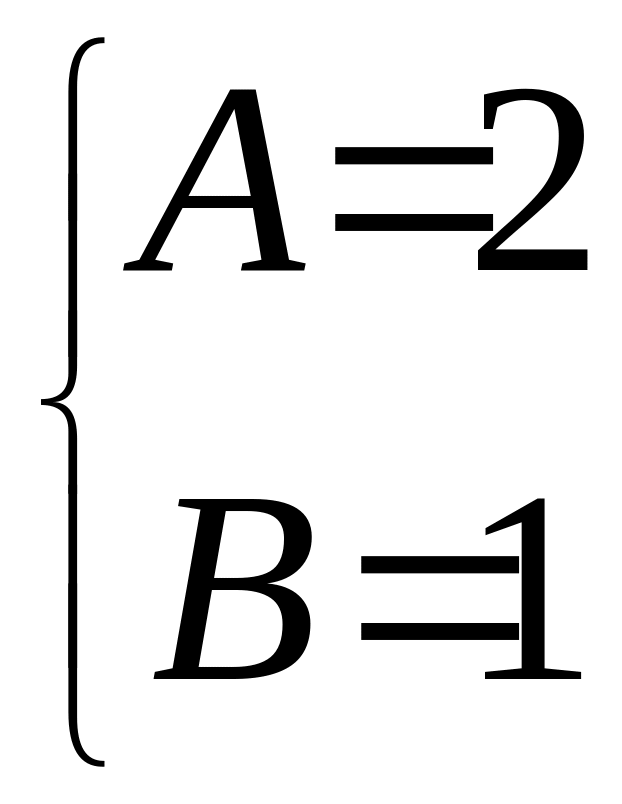Відповідь: .

2а) ;

; ; ; ;

; ; ;

;

; ; ;

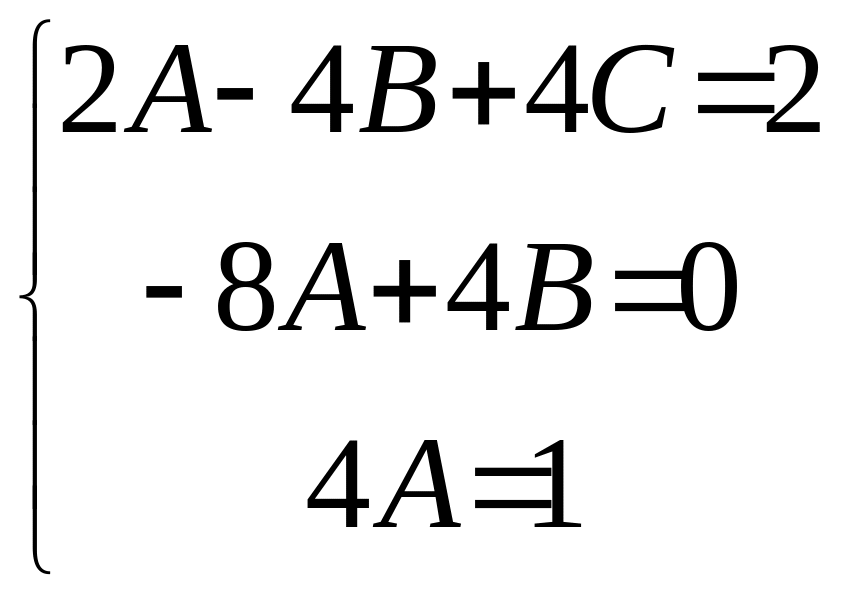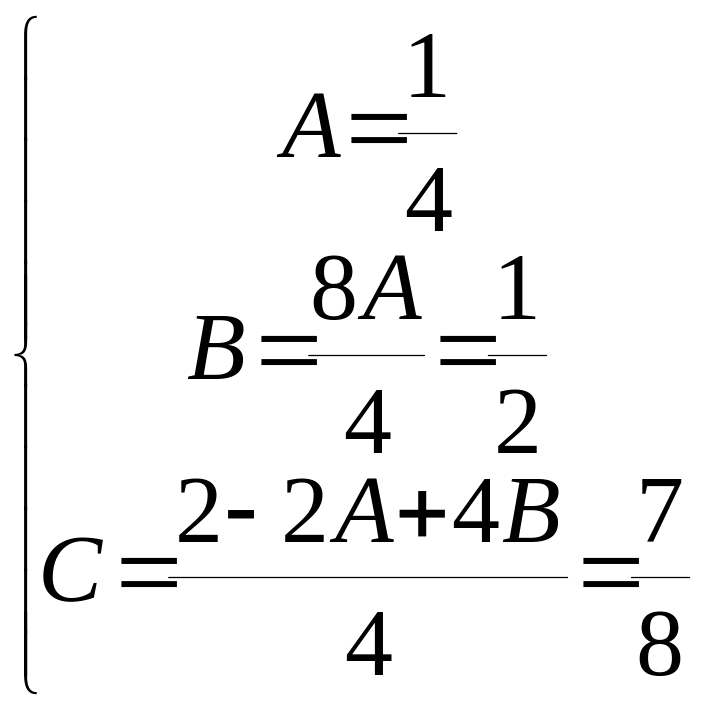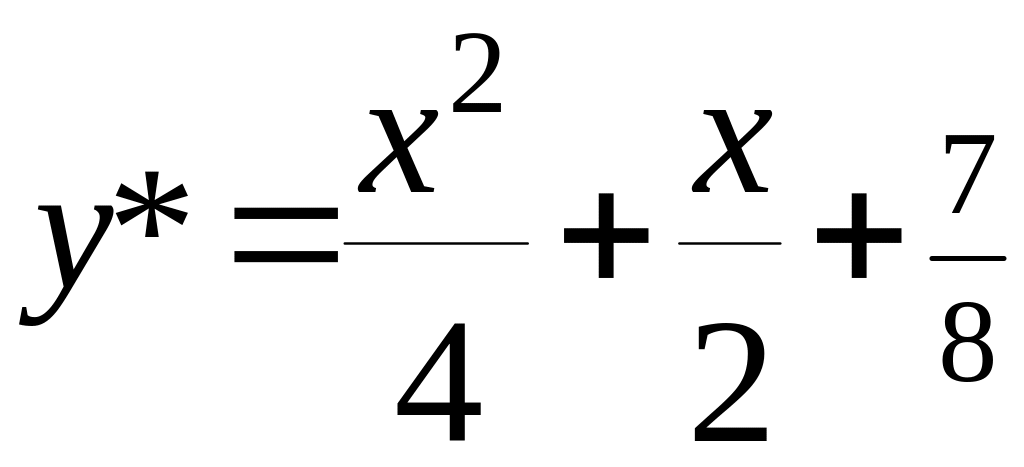Відповідь: .

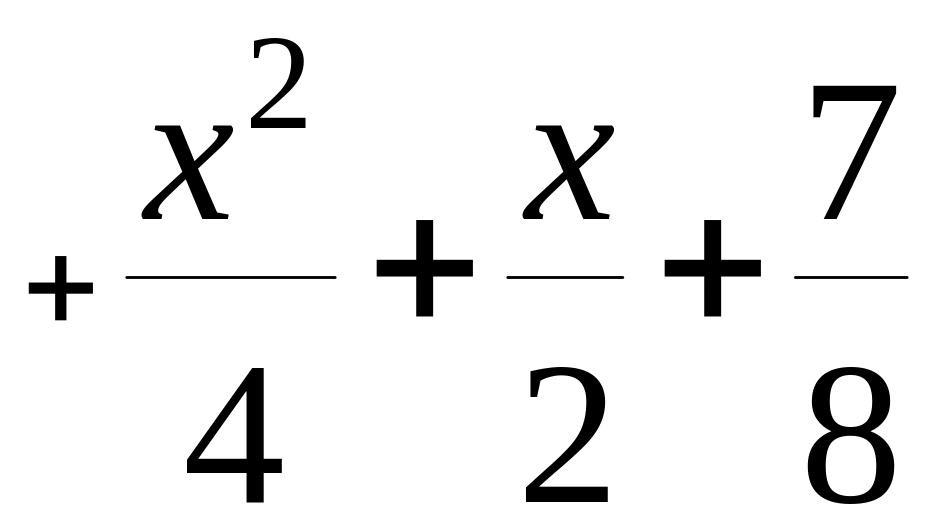2б) ;

: маємо подвійний збіг , отже = ;

.

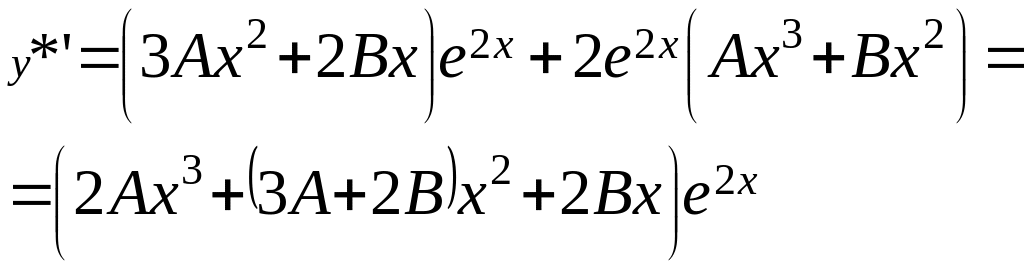
Підставляємо y*, та до 2б),скорочуємо на і прирівнюємо множники при однакових степенях х в лівій і правій частинах рівняння :

; ; ;

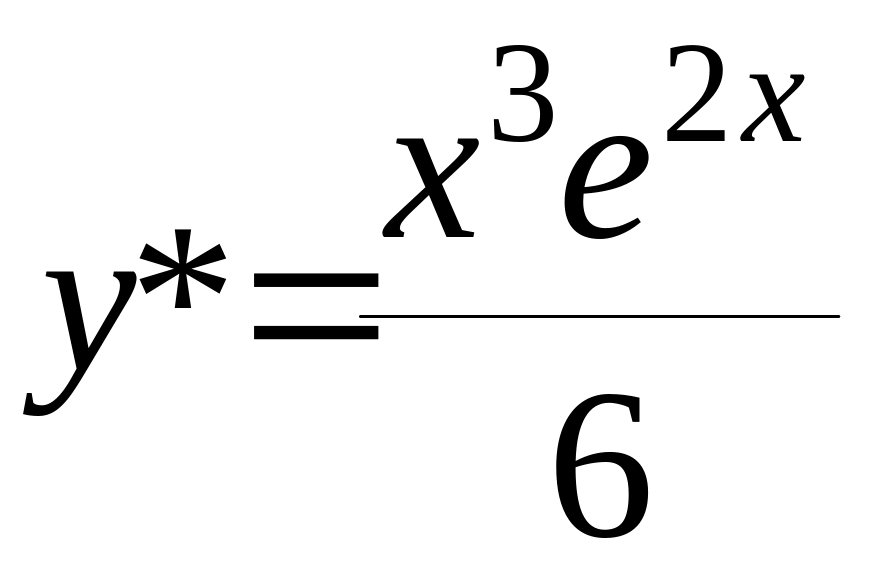Відповідь: .

2в) ;

; ; ; ;

; ;

;

підставляємо до 2в) та скорочуємо на :

+6 +9 =cosx;

прирівнюємо множники при та в лівій і правій частинах рівняння, знаходимо

А=-1,В=0, .

Відповідь: .

Взагалі , можна показати , що д.р.

має такий ч.р.: .

3а) ;

;в правій частині а=0,в=3 , отже шукаємо

, ; +

+ ; + ;

+ + = ;

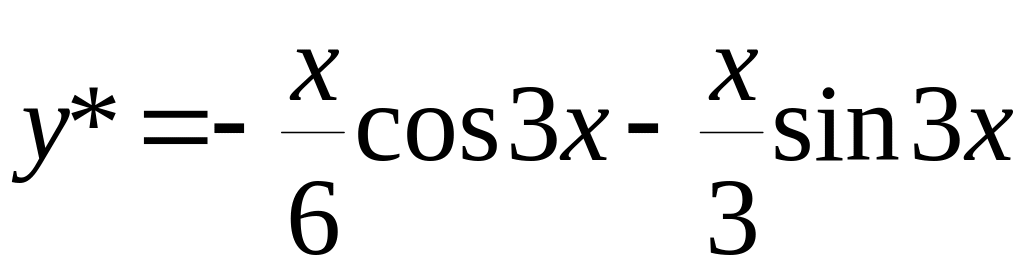.Враховуючи, що ,маємо

Відповідь: .

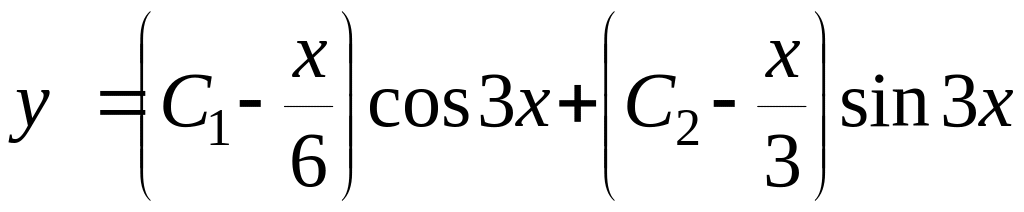Взагалі , можна показати , що д.р.

має такий ч.р.: .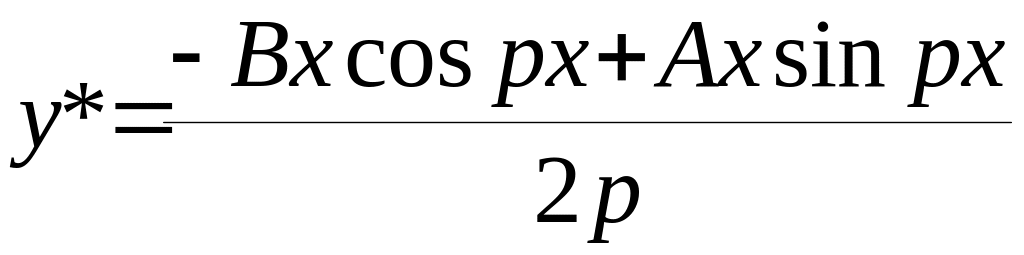

3б) ;

; ; ;

.

Пропонуємо самостійно показати, що .

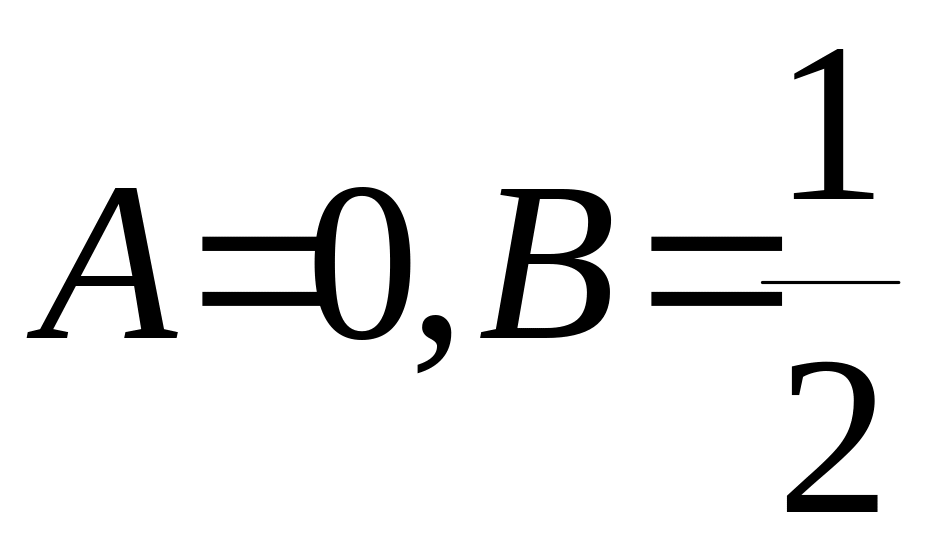Відповідь: .

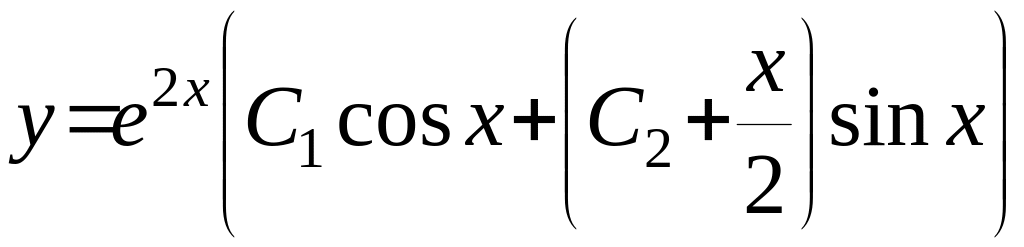3в) ;

; ; ;маємо збіг: , отже загальний вид правої частини 3в) треба множити на х,

щоб отримати = .

= .

= .

; ; ;

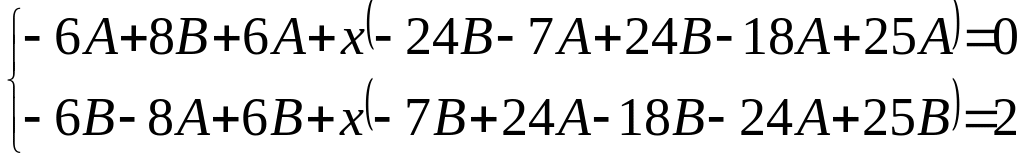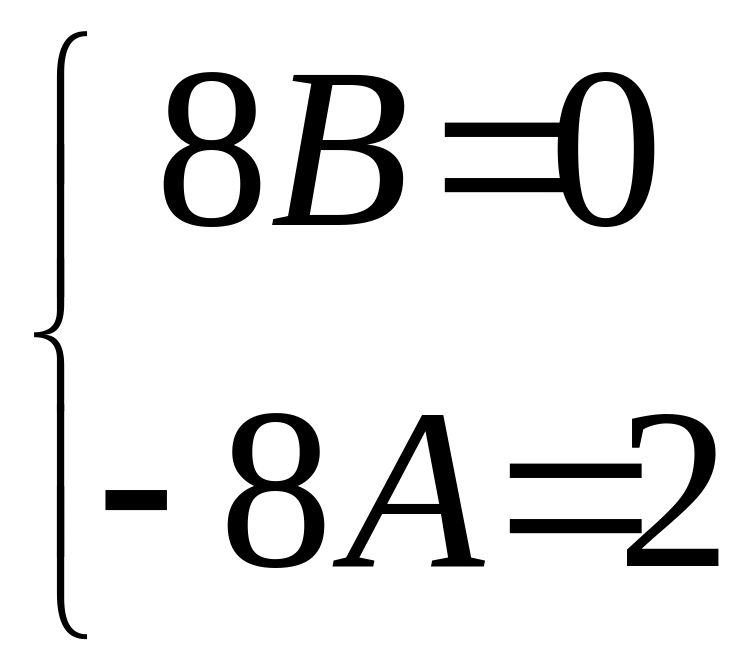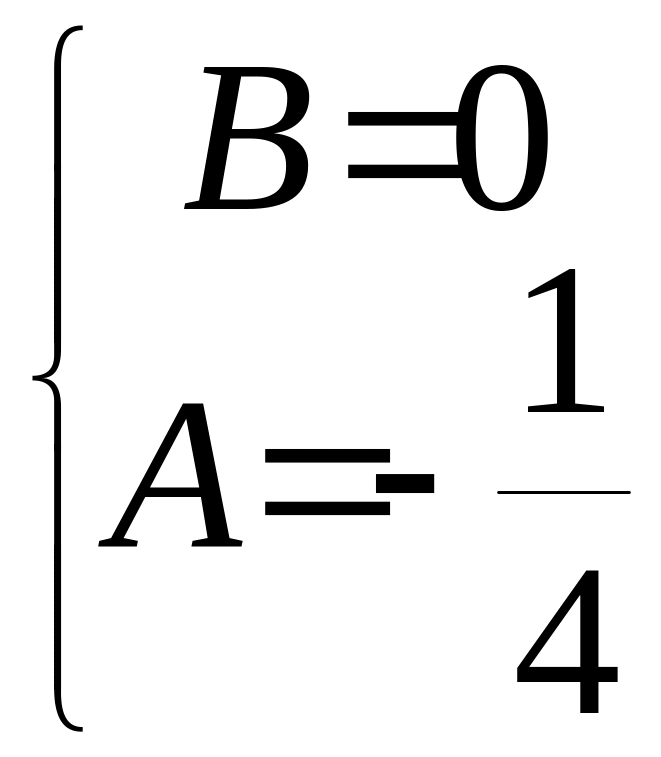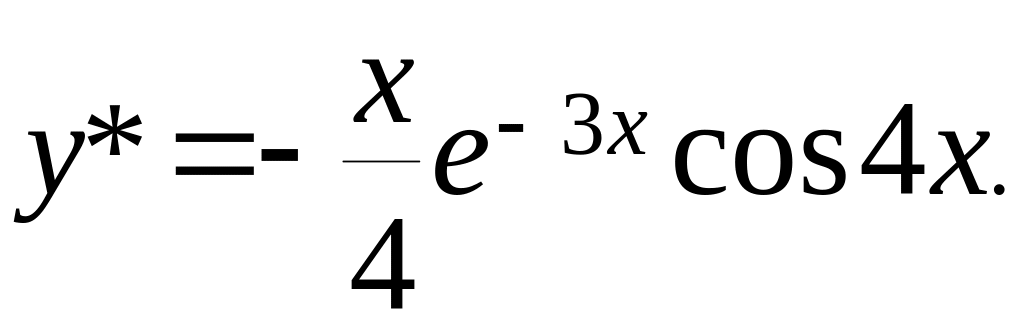
Відповідь: .

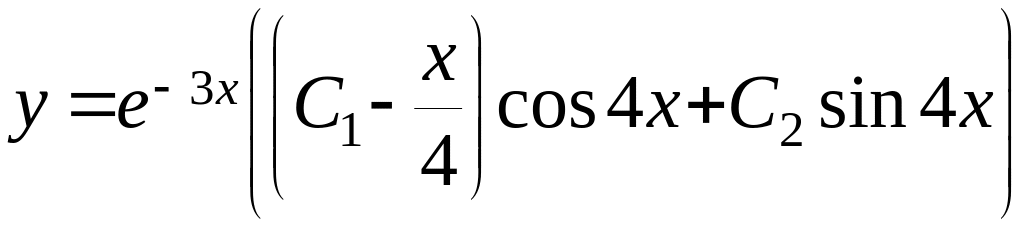Для знаходження загального розв’язкуку лінійного неоднорідного диференціального рівняння завжди можемо застосовувати метод варіації сталих (метод Лагранжа), але в випадках, коли

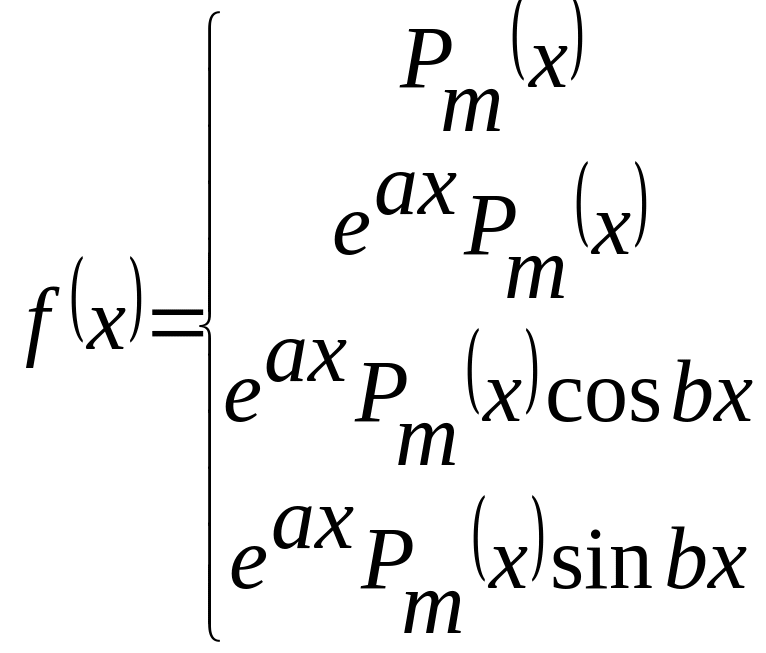, або є їх лінійною комбінацією, доцільним буває спосіб підбору.

В інших випадках користуємося методом Лагранжа,наприклад:

4) ; ; ; ; ;

.

, ,

, , .

,

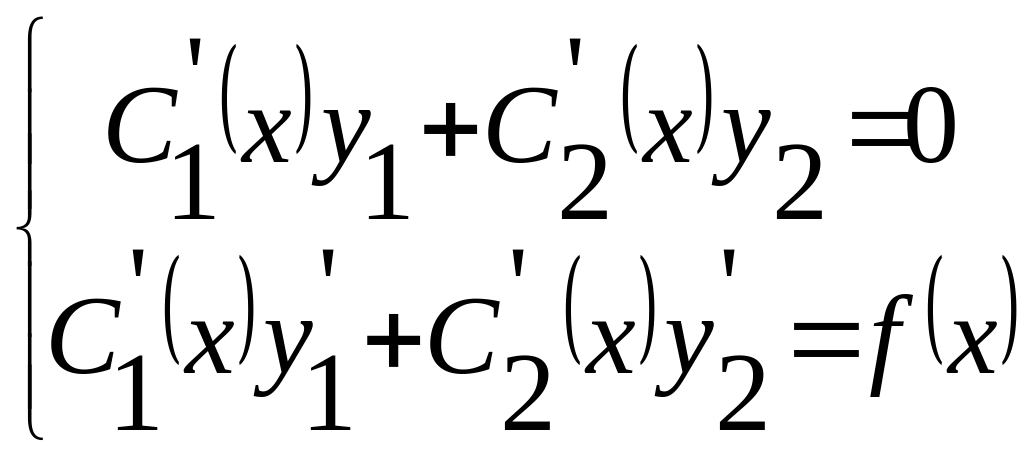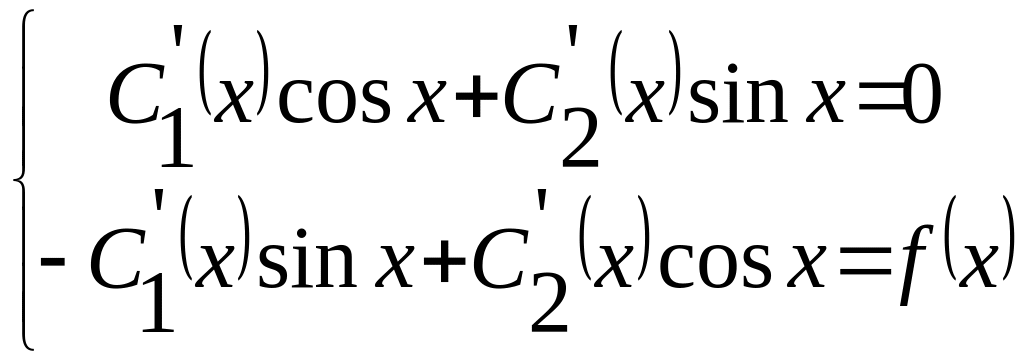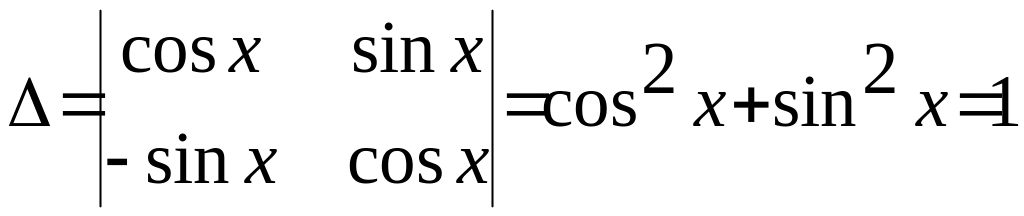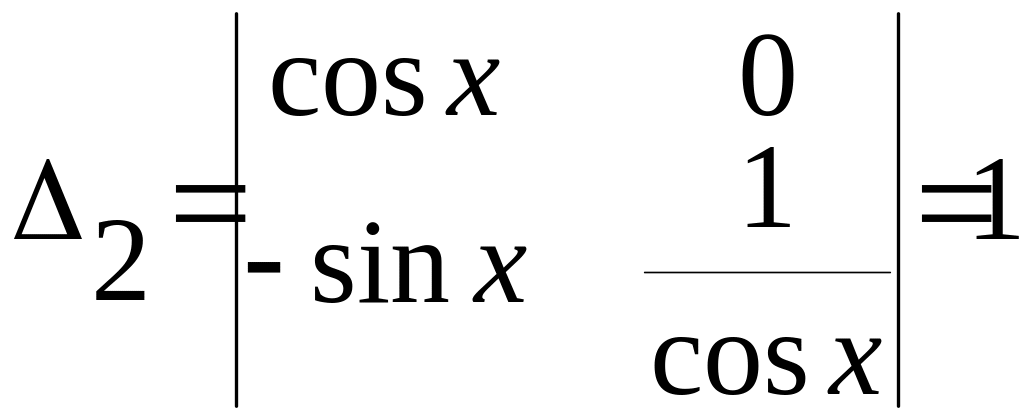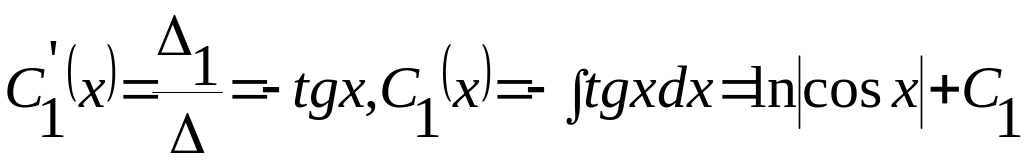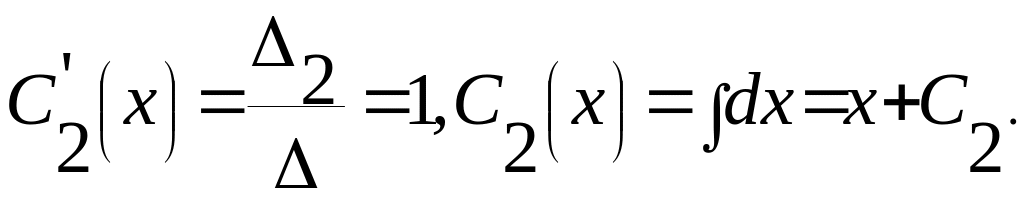
Відповідь:

Питання пошуку конкретного частинного розв’язку д.р. можливо поставити в двох видах:

а)задача Коші : за даними початковими умовами та ;

б)крайова задача :за даними значеннями шуканої функції, чи її похідної для двох значень аргумента:

та , або та , або та .