
- •О.Частинним розв’язком д.Р.(2,2) наз. Розв’язок , який отримують із загального при конкретному значенні за допомогою початкових умов.
- •2.1Рівняння з відокремлюваними змінними
- •2.2 Однорідні диференціальні рівняння
- •2.3 Лінійні рівняння першого порядку
- •2.4 Рівняння Бернуллі
- •Рівняння в повних диференціалах
- •Особливі розв’язки
- •3.1 Рівняння , які допускають зниження порядку
- •3.2Лінійні рівняння о. Д.Р. Виду
- •3.3Лінійні однорідні рівняння зі сталими коефіцієнтами
- •Випадок кратних коренів
- •3.4Лінійні неоднорідні рівняння зі сталими коефіцієнтами
- •Розділ 4
РОЗДІЛ1.
Основні поняття.
Означення.Диференціальним рівнянням(д.р.) називається рівняння, яке містить хоч би одну похідну або диференціал невідомої функції.
Oчевидно, що найпростіше д.р. має вид:dy=0 .
Іші приклади:

Невідома функція та незалежні змінні можуть і не входити до рівняння в явному вигляді,а от присутність похідної чи диференціала необхідна.
Означення. Д.р.називається звичайним, якщо невідома функція залежить лише від однієї незалежної змінної.
Саме на звичайних д.р. ми і зосередимо свою увагу.
Всяке д.р.має нескінченну кількість розв’язків, сукупність яких називають.загальним розв’язком(з.р.) або загальним інтегралом д.р.Кожен окремий розв’язок називається частинним розв’язком(ч.р.).З геометричної точки зору кожен з ч.р.визначає на координатній площині інтегральну криву.
Означення. Порядком д.р.наз.найвищий з порядків похідних,які входять до цього рівняння. Так д.р.(2)та(4)другого,(3)третього, а (1)першого порядків.
РОЗДІЛ 2.
Диференціальні рівняння першого порядку.
Д.р.першого порядку має такий загальний вигляд:
![]()
![]() (2.1)
(2.1)
Якщо це рівняння розв’язується відносно похідної,то його можемо записати так:
![]() (2.2)
(2.2)
Для рівняння (2,2) справджується теорема Коші:
Т.Якщо
![]() та
та
![]() неперервні в області D
,яка містить точку
неперервні в області D
,яка містить точку
![]() ,то існує єдиний розвязок рівняння
,який
задовольняє умову
,то існує єдиний розвязок рівняння
,який
задовольняє умову
![]() .
.
О.Умова ,яка полягає в тому ,що для р-ня (2.2) наз. початковою.
О.Загальним
розв’язком
д.р. (2.2)
наз. функція
![]() (*),яка
залежить від довільної сталої с
та задовольняє умови:
(*),яка
залежить від довільної сталої с
та задовольняє умови:
1)для довільної с вона є розв’язком (2.2),
2) для
довільних початкових умов
існує таке значення
![]() ,що
,що![]() .
.
О.Частинним розв’язком д.Р.(2,2) наз. Розв’язок , який отримують із загального при конкретному значенні за допомогою початкових умов.
Д.р.(2.2)
разом з умовою
![]() наз. задачею
Коші.
наз. задачею
Коші.
Наприклад,
д.р. (1) в вигляді (2.2) буде :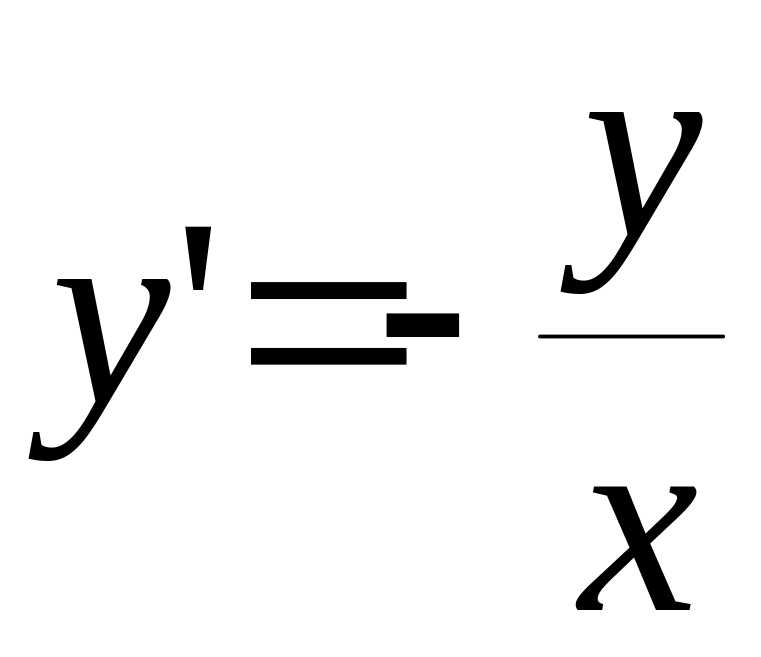 ;
;
функції
![]() -
-![]() та
та
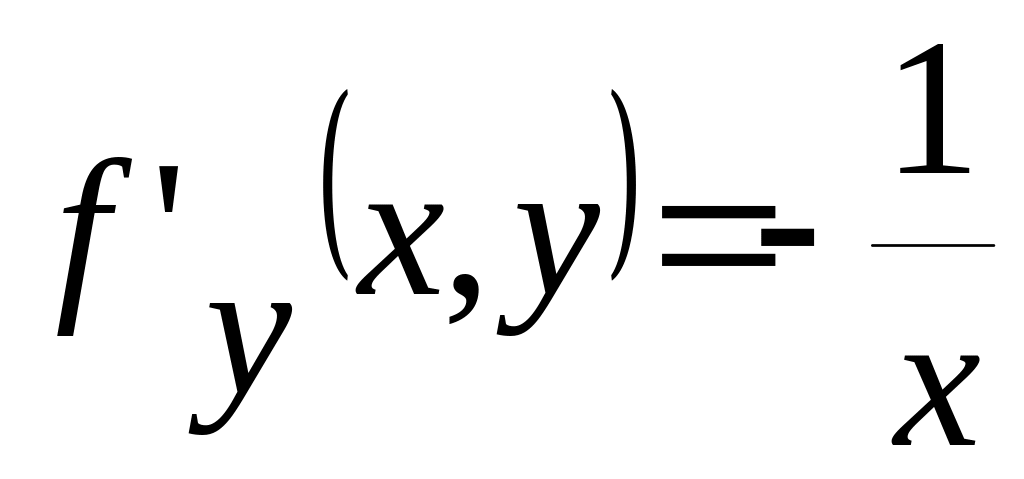 неперервні в довільній області, яка не
перетинає вісі ординат. Легко перевірити,
що
неперервні в довільній області, яка не
перетинає вісі ординат. Легко перевірити,
що
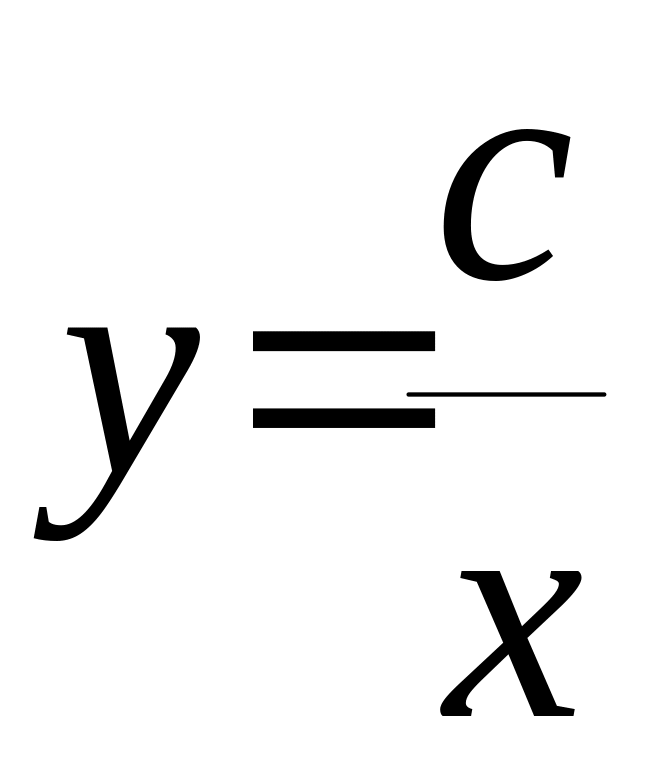 є загальним розв’язком д.р. (1), бо
є загальним розв’язком д.р. (1), бо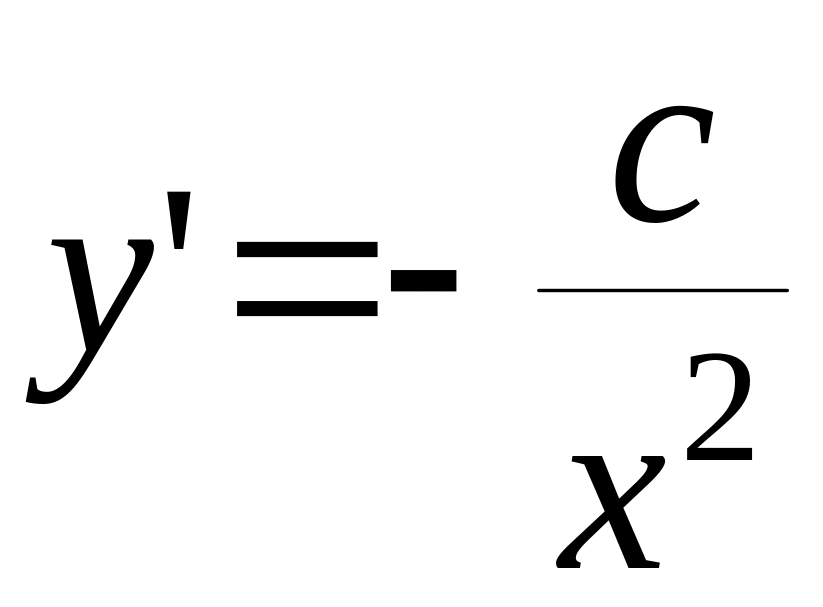 ,
отже
,
отже
 .
.
Візьмемо,
наприклад,
![]() ,
тоді маємо:
,
тоді маємо: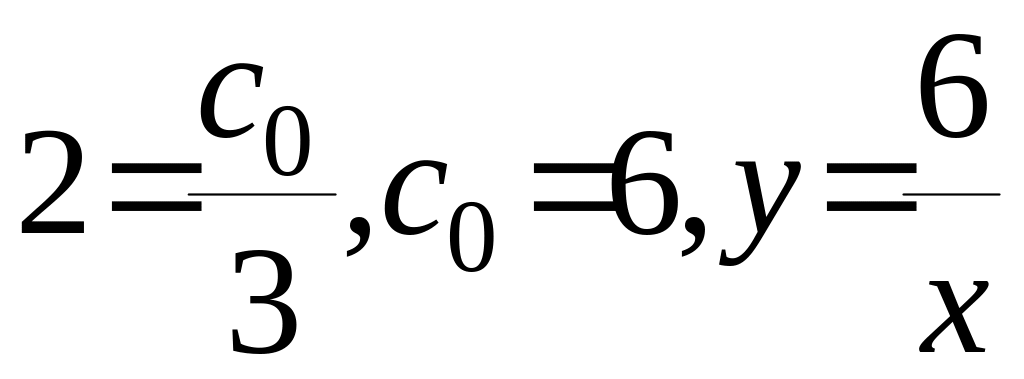 є частинний розв’язок .
є частинний розв’язок .
Інакше
кажучи, задача Коші :
;![]() має розв’язок
має розв’язок

Буває,що незручно або просто неможливо отримати розв’язок в вигляді (*),але легко дістати неявну функцію Ф(x,y)=с, яка наз. загальним інтегралом д.р.Відповідно, Ф(x,y)= наз. частинним інтегралом д.р.
2.1Рівняння з відокремлюваними змінними
О.
Д.р. виду
![]() (2.1.1)
(2.1.1)
наз. рівнянням з відокремленими змінними.
Наприклад
:
![]()
![]() (2.1.2)
(2.1.2)
(2.1.1)
є рівність двох диференціалів (бо dy=![]() dx)
деяких
функцій від x,
невизначені інтеграли від яких
відрізняються на довільну сталу C
dx)
деяких
функцій від x,
невизначені інтеграли від яких
відрізняються на довільну сталу C
![]() =
=![]() +C
(2.1.3)
+C
(2.1.3)
У випадку (2.1.2) маємо
![]()
![]() +С,
+С,
![]() ,
Відповідь:
,
Відповідь:
![]() -загальний
інтеграл або Відповідь:
-загальний
інтеграл або Відповідь:
![]() -функція
в явному виді.
-функція
в явному виді.
Якщо в (2.1.3) хоч один з невизначених інтегралів не виражається через скінченну кількість елементарних функцій (“не береться”) то кажуть,що рівняння розв’язано в квадратурах(“квадратура”-синонім терміну “невизначений інтеграл”).Наприклад:
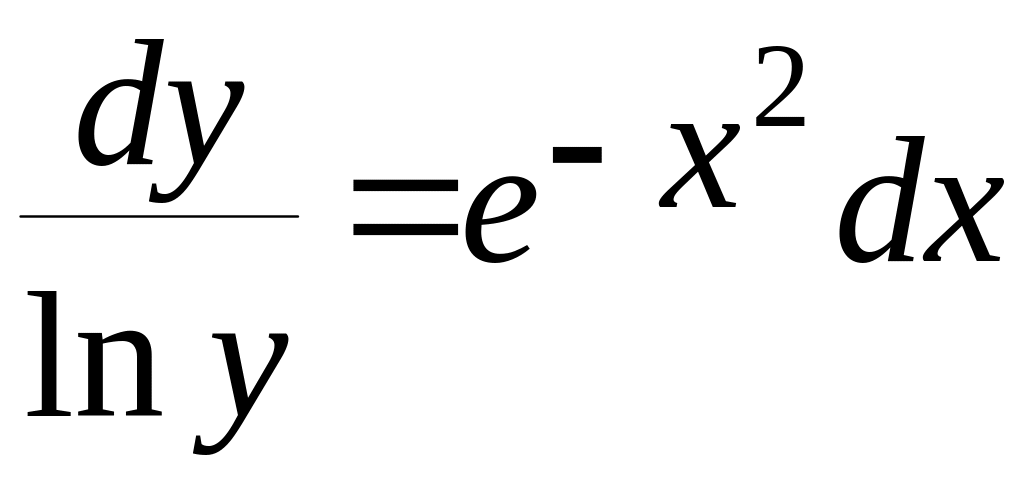 ,
(2.1.4)
,
(2.1.4)
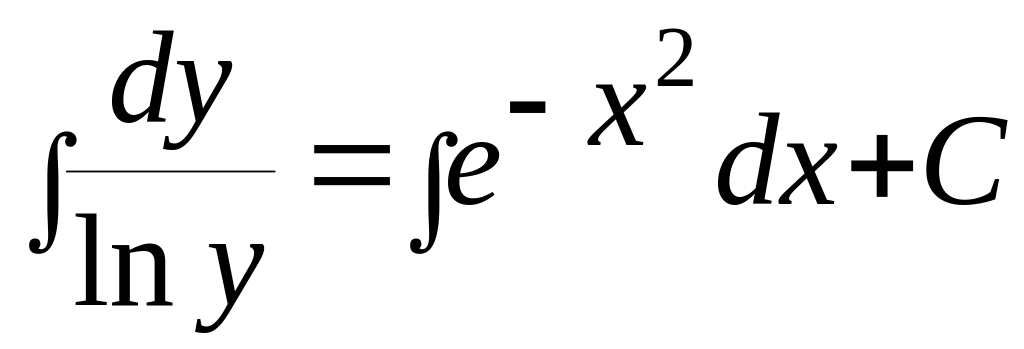 ,
Відповідь:
,
Відповідь:
 -
-![]() =C,
що є загальним
інтегралом д.р
(2.1.4).
=C,
що є загальним
інтегралом д.р
(2.1.4).
О. Д.р. яке шляхом алгебраїчних операцій зводиться до виду (2.1.1), наз. д.р. з відокремлюваними змінними.
Приклади:
1)![]() =
=
![]() (2.1.5)
(2.1.5)
поділивши
обидві частини д.р. на
![]() ,маємо:
,маємо:
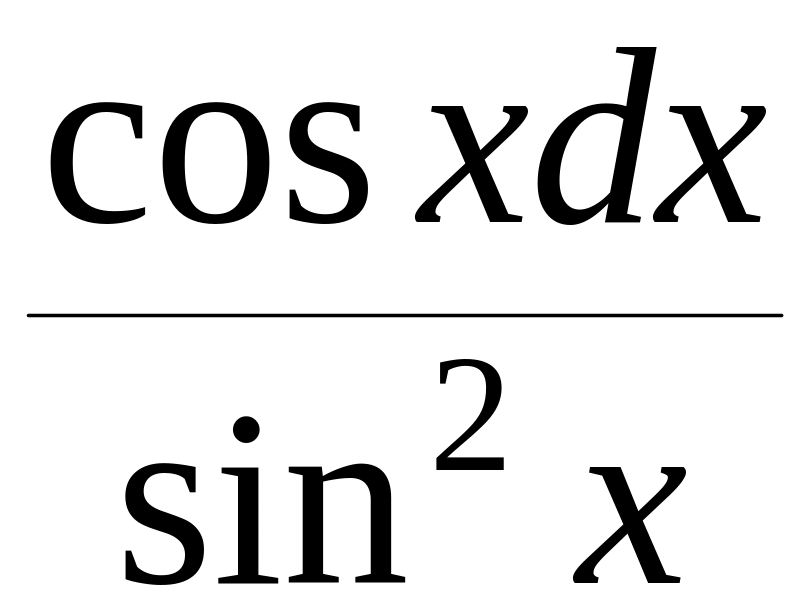 =
= ,
,
 =
=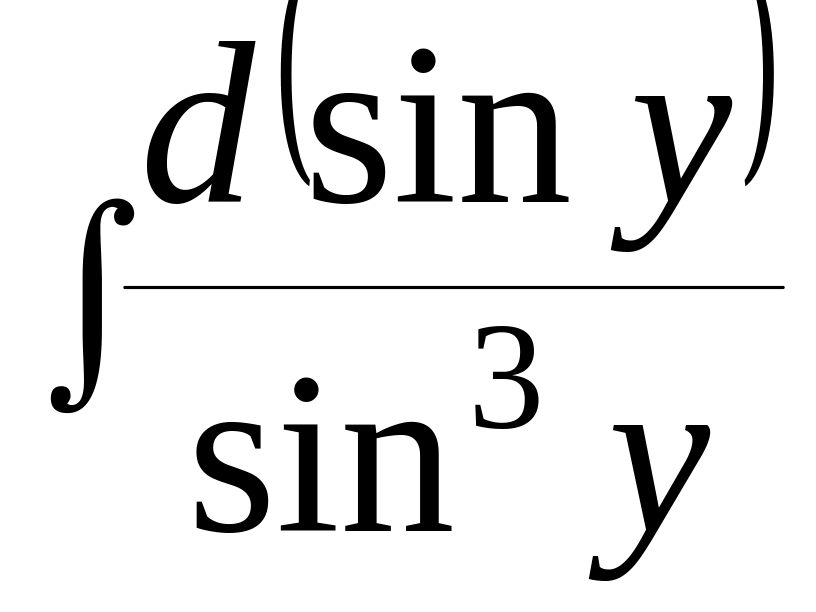 ,-
,-
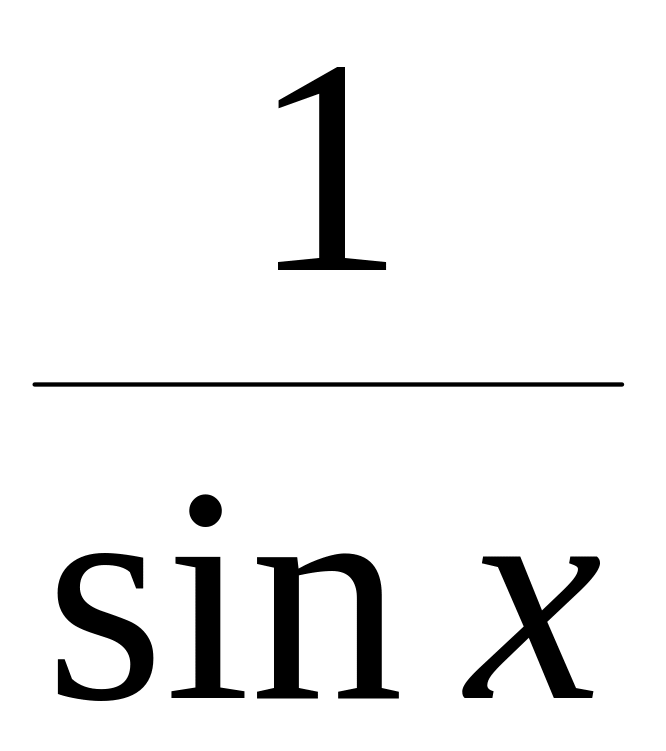 =-
=-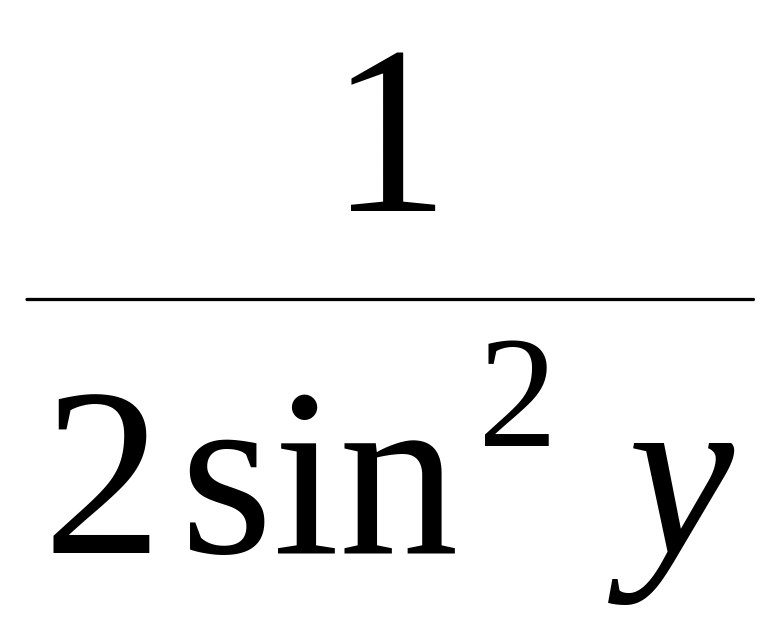 +C
,
+C
,
Відповідь: - =C.
2)![]()
![]() +
+
![]()
![]() =0
(2.1.6).
=0
(2.1.6).
Врахуємо,
що
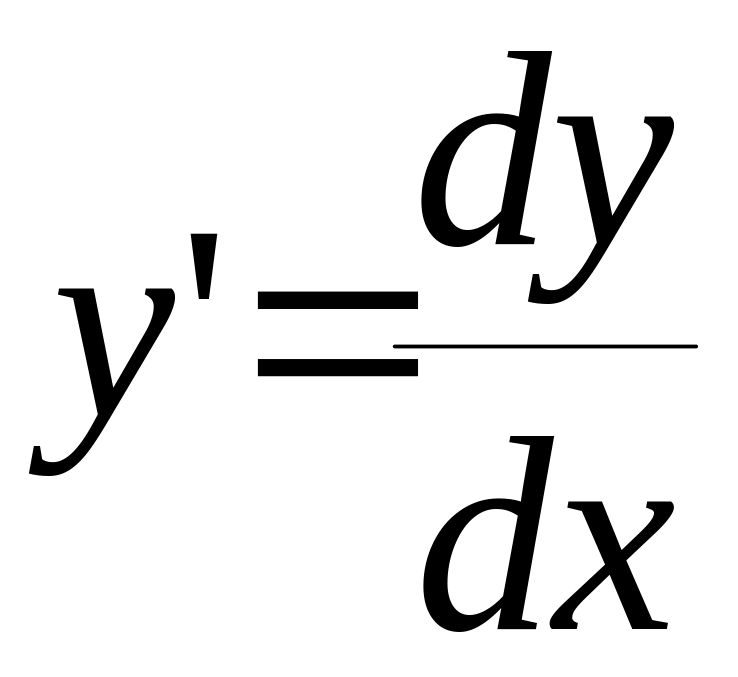 та поділивши на
і,
помноживши на
та поділивши на
і,
помноживши на
![]() ,
отримаємо
,
отримаємо
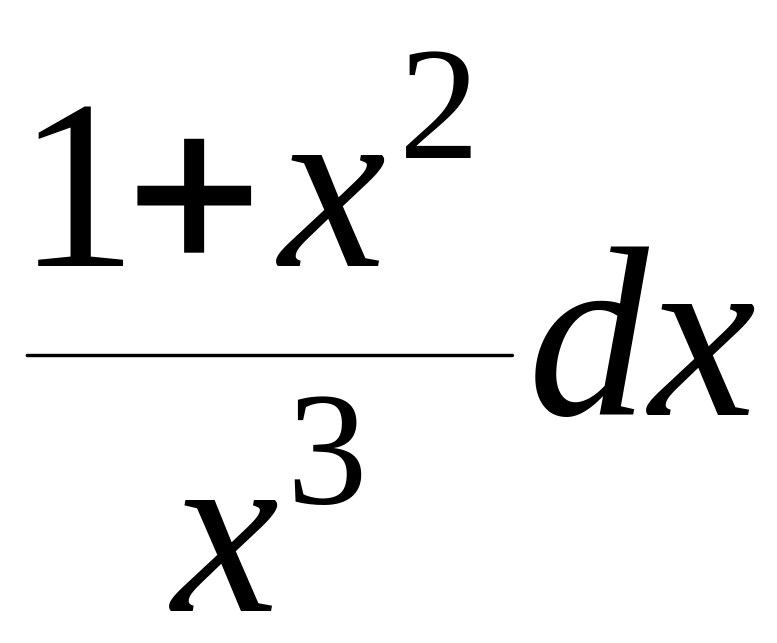 =
=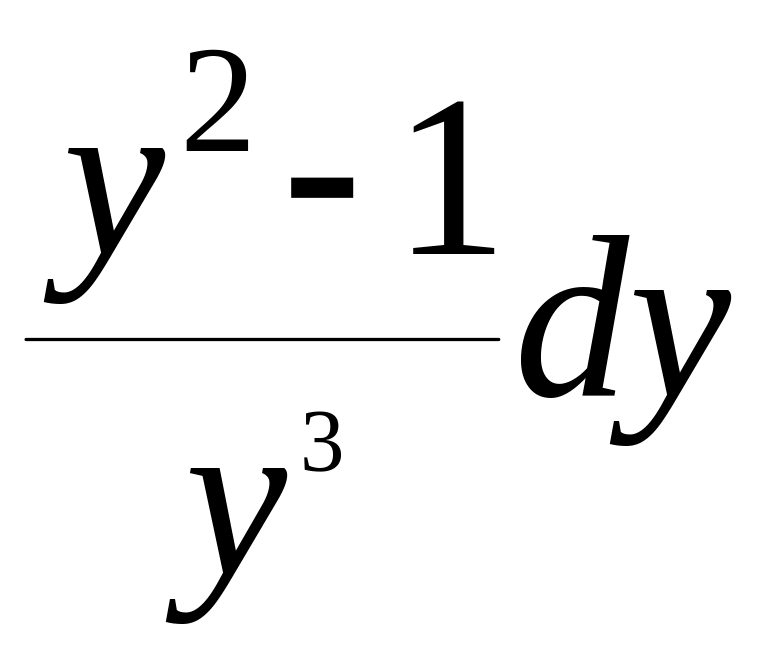 ,
,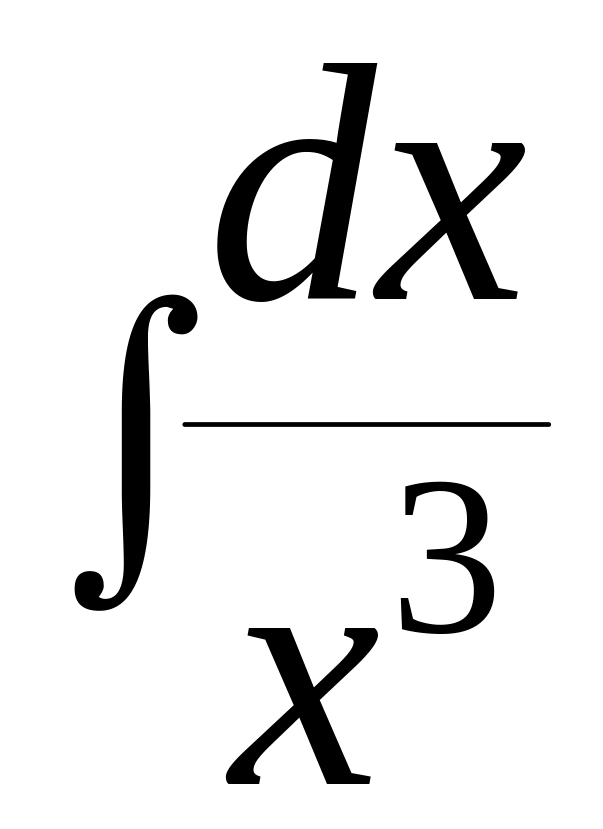 +
+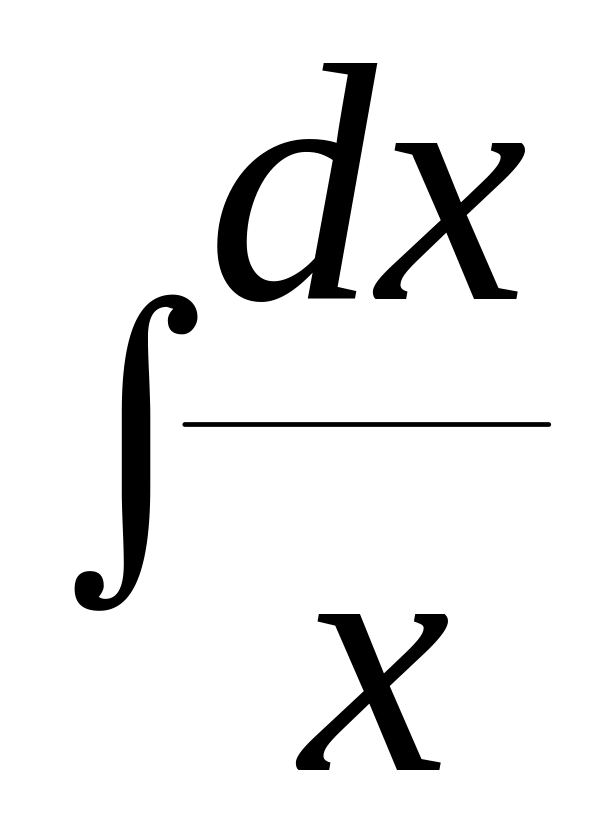 =
=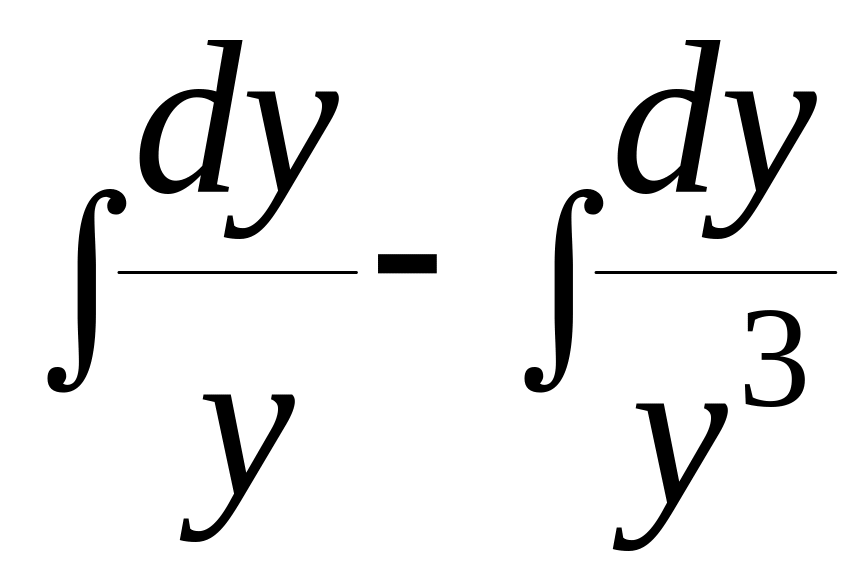 ,
,
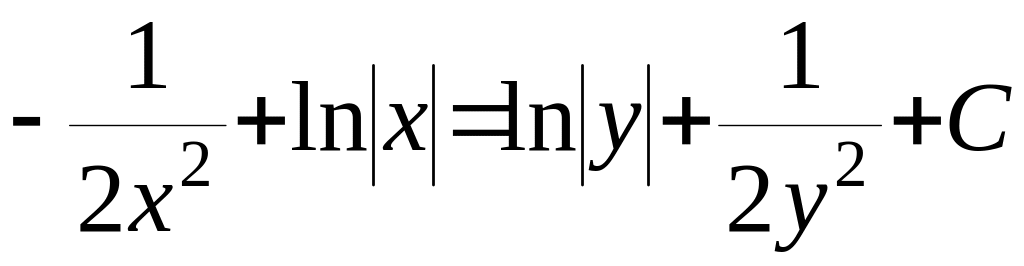 ,
і остаточно :
Відповідь:
,
і остаточно :
Відповідь:
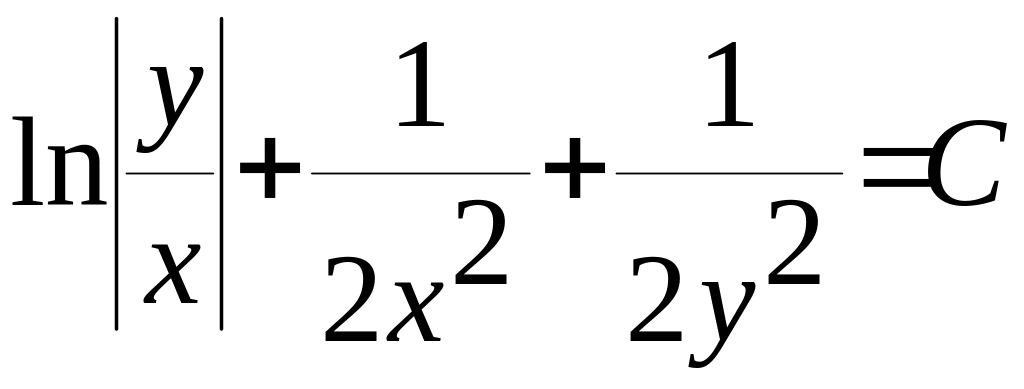 ,
що є загальним інтегралом д.р. (2.1.6).
,
що є загальним інтегралом д.р. (2.1.6).
3)![]() +
+![]() =0
,
(2.1.7)
=0
,
(2.1.7)
 =
=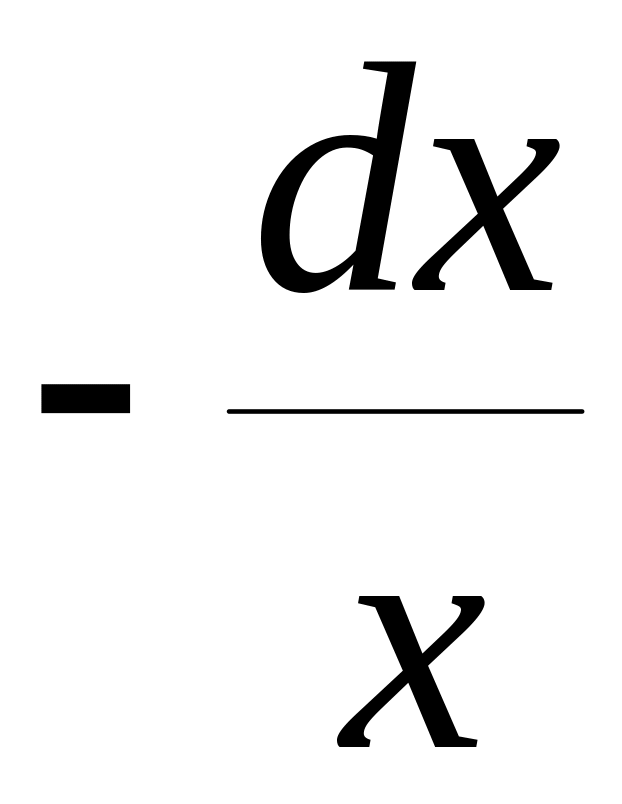 ,
,
![]() =-
=-![]() +
+![]() ,
,
![]() =
=![]() ,
Відповідь:
y=
,
Відповідь:
y=
![]() .
.
4)
![]() (2.1.8),
(2.1.8),
=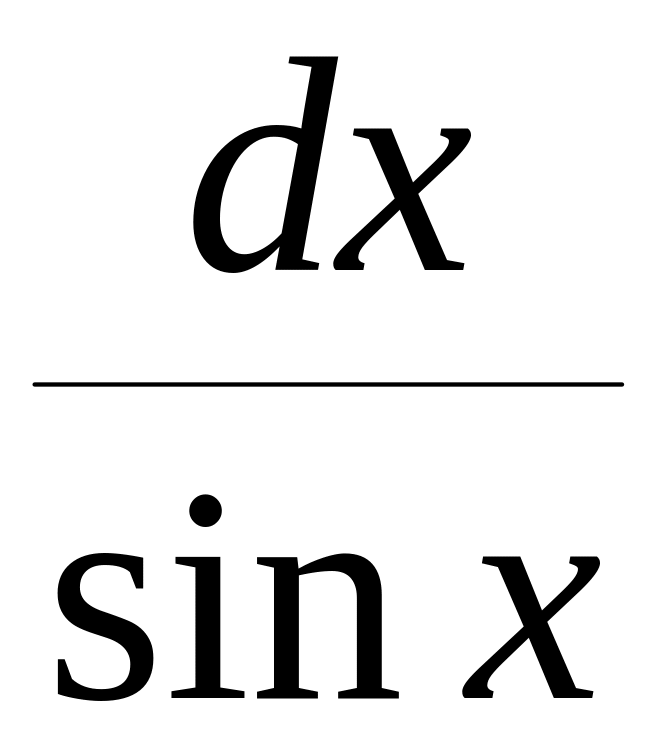 ,
, =
=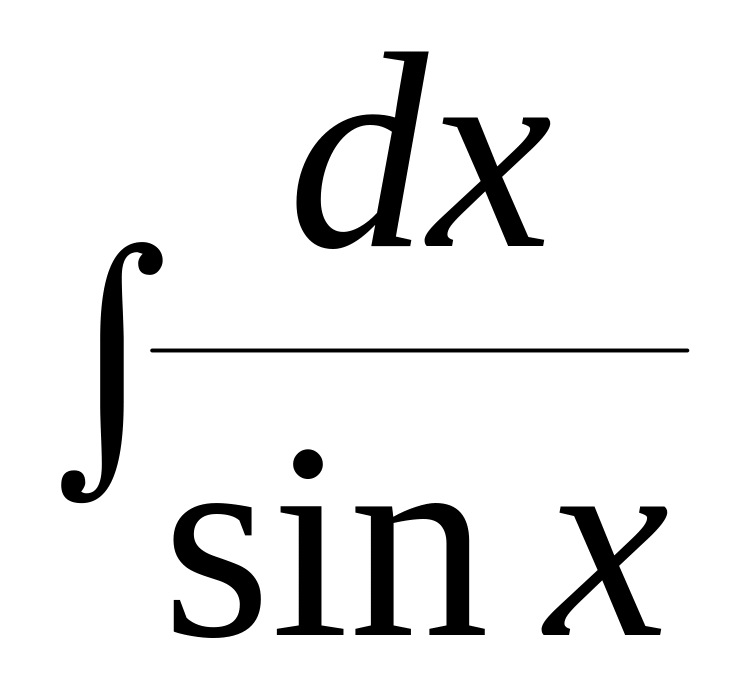 ,
=
,
=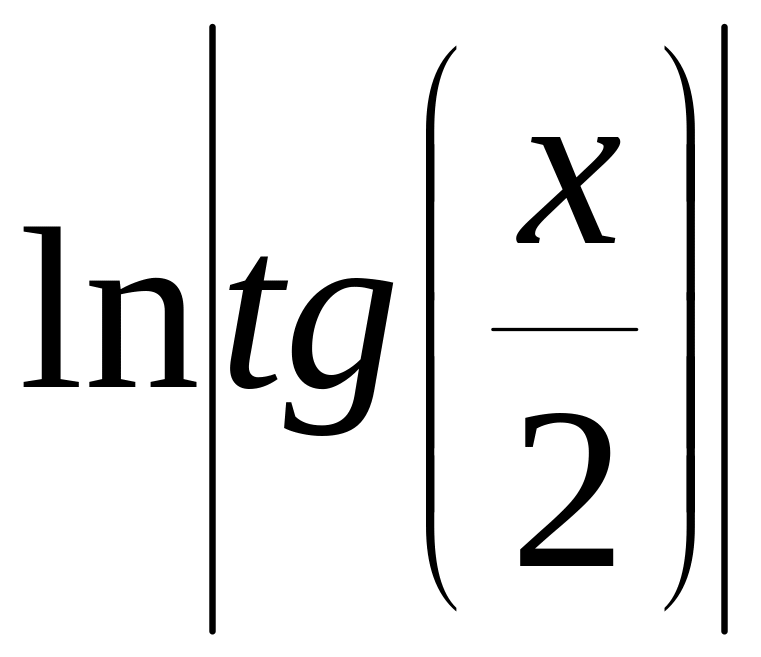 +
+![]() ,
,
 Відповідь:
Відповідь:
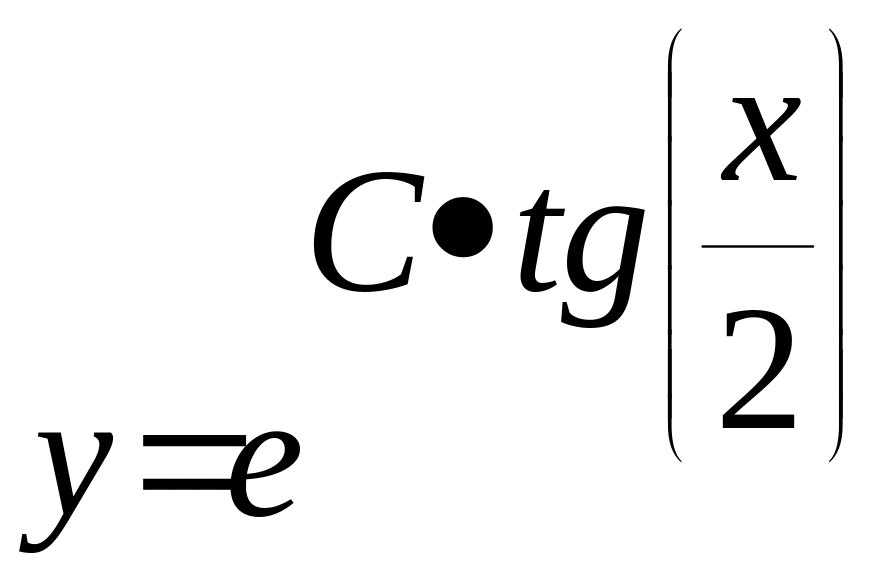 .
.
5)Задача
Коші :
 ;
;
 =
=![]() ,
,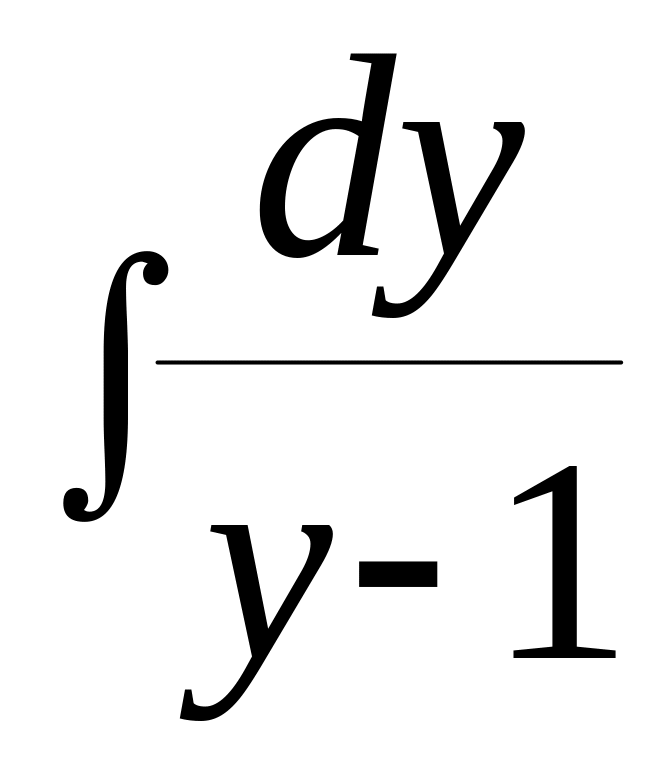 -
- =
,
=
,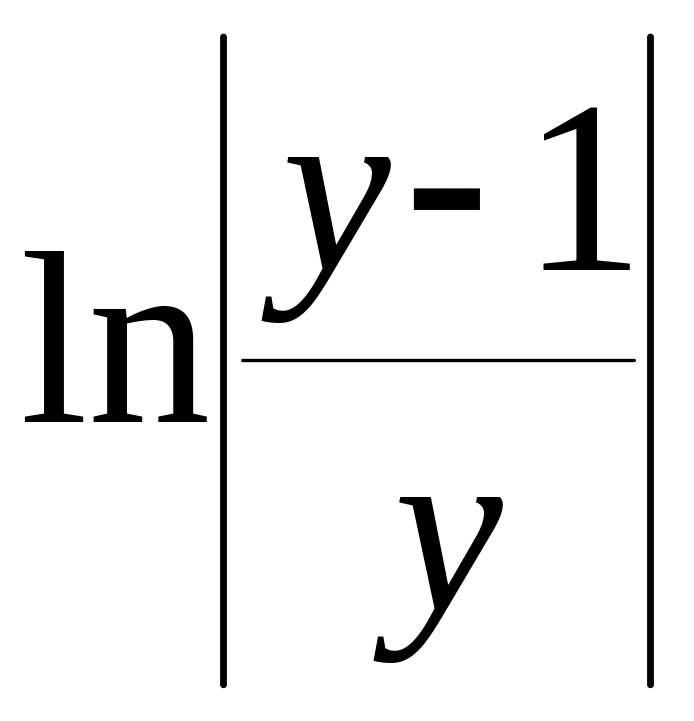 =
=![]() ,
,
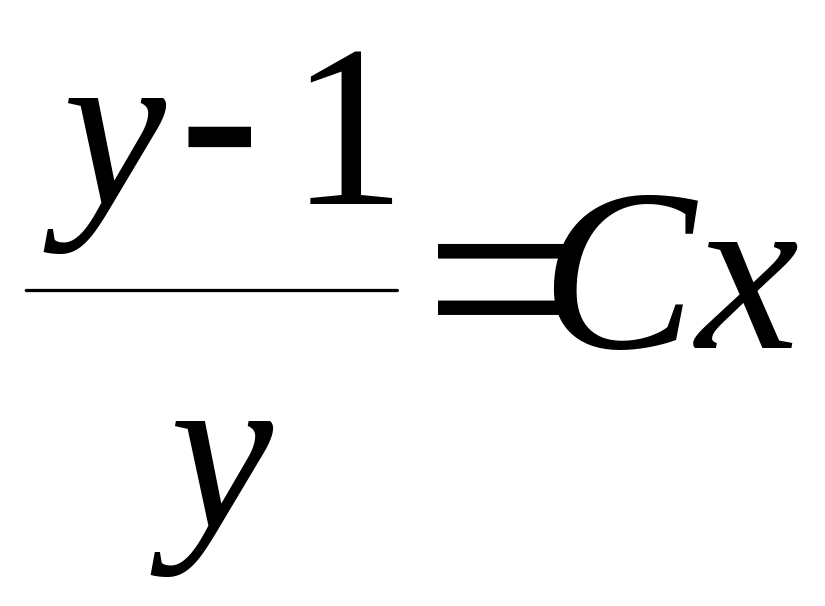 (*),
(*),
Відповідь:
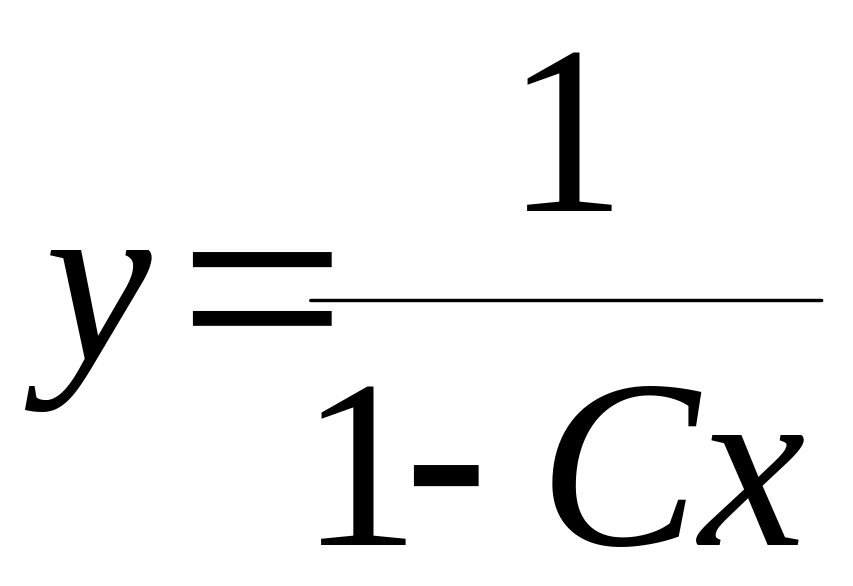 (**),
(**),
підставимо
початкові умови в (*)
: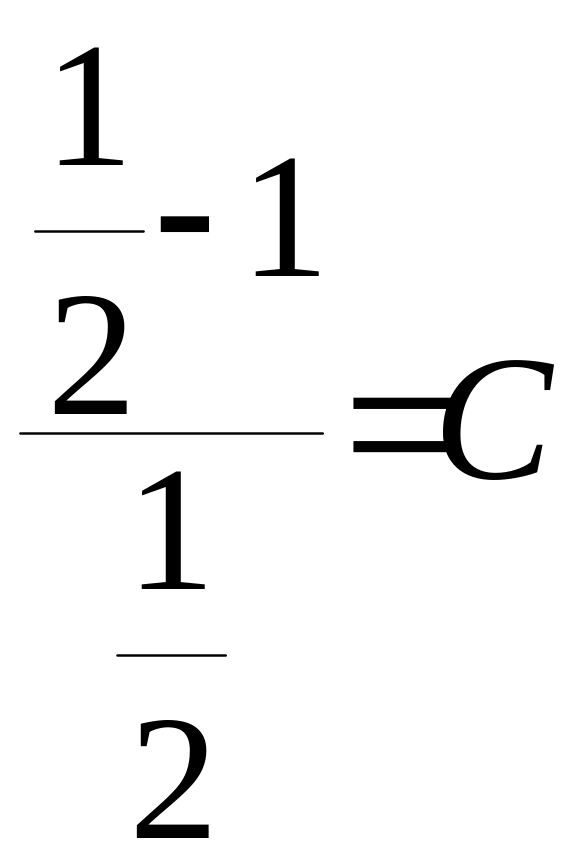 ,
С=-1
,
Відповідь:
,
С=-1
,
Відповідь:
 ,що
і є розв’язком задачі Коші тобто
частинним розв’язком д.р. В прикладах
1)-4) ми давали загальні розв’язки.
,що
і є розв’язком задачі Коші тобто
частинним розв’язком д.р. В прикладах
1)-4) ми давали загальні розв’язки.
До д.р. з відокремлюваними змінними зводяться д.р. виду
![]() ,
(2.1.9)
,
(2.1.9)
де
a
та b
є константи. Для зведення робиться
заміна :
![]() ,
,
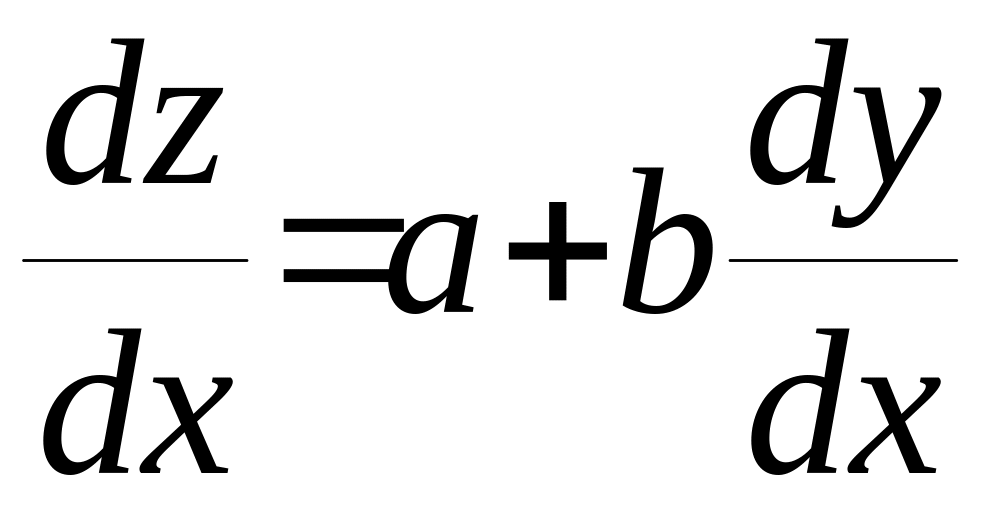 .Тоді
(2.1.9) матиме вид :
.Тоді
(2.1.9) матиме вид :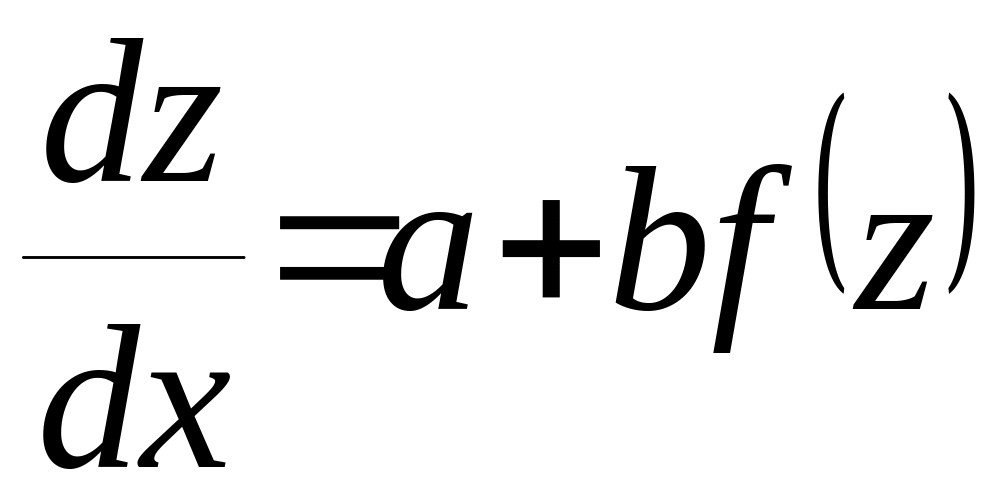 ,
а це вже є д.р. з відокремлюваними
змінними.
,
а це вже є д.р. з відокремлюваними
змінними.
Наприклад:
1)![]()
![]() ,
,![]() ,
і
д.р. прийме вигляд:
,
і
д.р. прийме вигляд: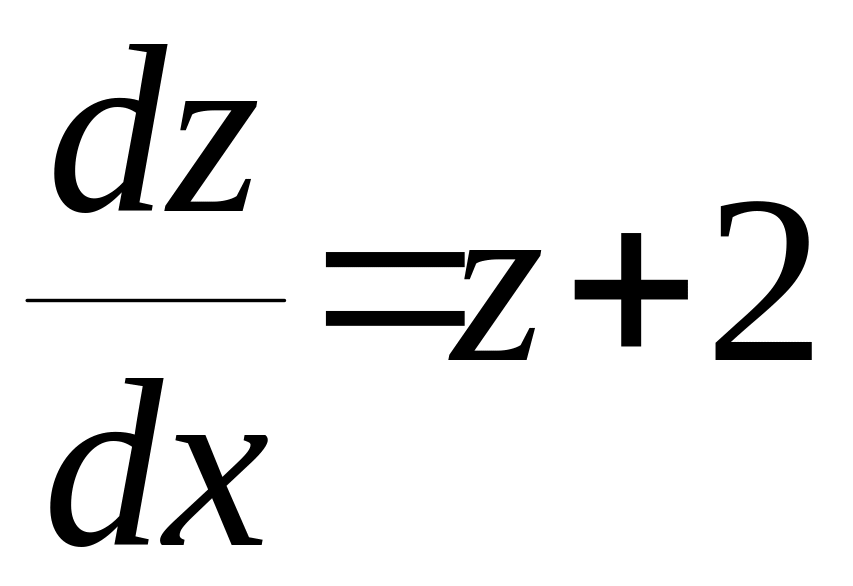 ,
,
 .
Після інтегрування маємо :
.
Після інтегрування маємо :
![]() ,
,
 ,
,
![]() ,
,
![]() ,
Відповідь:
,
Відповідь:
![]() .
.
2)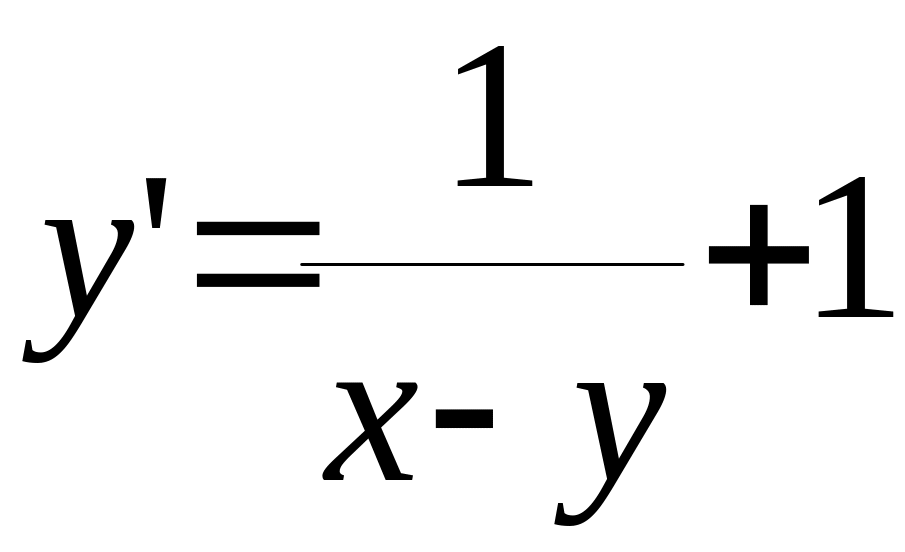 ,
,
![]() ,
,![]() ,
і д.р. прийме вигляд:
,
і д.р. прийме вигляд: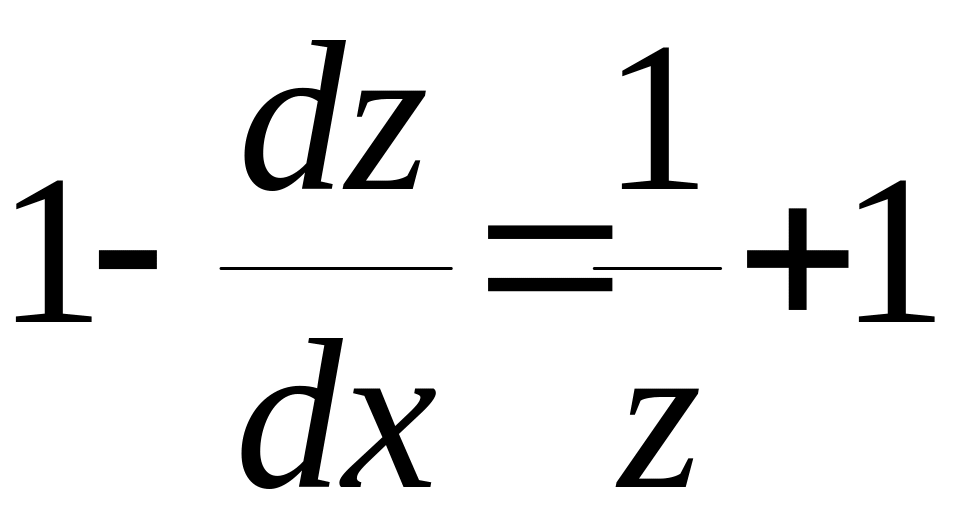 ,
,
![]() .
Після інтегрування маємо :
.
Після інтегрування маємо :![]() ,
Відповідь:
,
Відповідь:
![]()
Крім д.р. з відокремлюваними змінними існують ще класи д.р.першого порядку ,що розв’язуються, хоча б у квадратурах .Розглянемо деякі з них.
