5 Оптимизация контуров регулирования

5.1 Оптимизация контура тока якоря

Оптимизацию системы, построенной по принципу подчинённого регулирования, начинаем с внутреннего контура тока якоря. Структурная схема контура представлена на рисунке 5.1

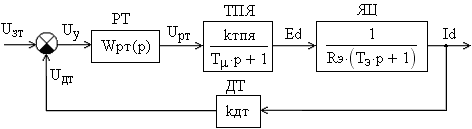
Рисунок 5.1 – Структурная схема контура тока якоря

РТ – регулятор тока;

ТПЯ – тиристорный преобразователь якоря двигателя;

ЯЦ – якорная цепь двигателя;

ДТ – датчик тока;

Оптимизация контура тока якоря на модульный оптимум проводится при следующих допущениях:

– все малые постоянные времени находятся в тиристорном преобразователе:

;

– датчик тока считаю безынерционным;

– двигатель заторможен (E_д = 0).

Определим тип регулятора тока, найдя его передаточную функцию:

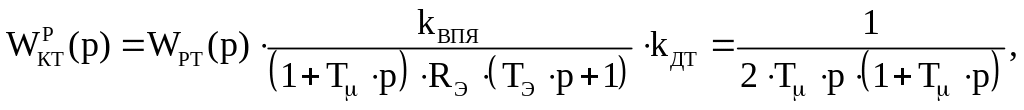(5.1.1)

тогда

(5.1.2)

где (5.1.3)

Полученной передаточной функции соответствует регулятор тока ПИ-типа. С этим регулятором система астатична по заданию и по возмущению (без учета действия внутренней обратной связи по ЭДС).

П ередаточная функция замкнутого контура тока имеет вид:

(5.1.4)

Т. к. величина Т_ мала, то слагаемым можно пренебречь, тогда считая , получаем

(5.1.5)

где Т_т = 2∙Т_µ =2∙0,01=0,02 (с) – эквивалентная постоянная времени настроенного на модульный оптимум контура тока.

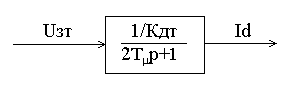
Рисунок 5.2 - Структурная схема замкнутого контура тока

Расчёт параметров регулятора тока:

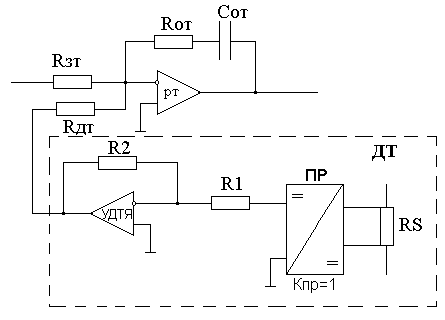
Рисунок 5.3а – Решающая цепь регулятора тока якоря

Коэффициент регулятора тока

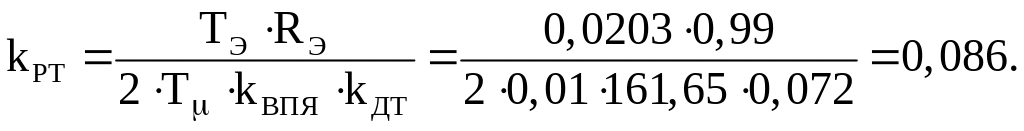(5.1.6)

З адаюсь величиной ёмкости конденсатора в цепи обратной связи операционного усилителя регулятора тока

Сопротивление резистора в цепи обратной связи операционного усилителя регулятора тока:

(5.1.7)

Сопротивление в цепи датчика тока:

(5.1.8)

Сопротивление в цепи задания тока нахожу из условий установившегося режима, в котором , откуда:

. (5.1.9)

Считая получаем:

R_зт = R_дт = 118 кОм.

Коэффициент усилителя датчика тока якоря определён в разделе 3.

(5.1.10)

Принимаем R₁ = 5 кОм, тогда R₂ = R₁∙k_удтя = 5∙47,8 = 239 кОм.

Рассмотрим реальный датчик тока на базе трансформатора тока.

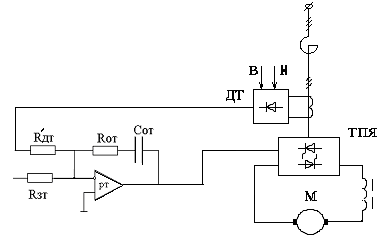
Рисунок 5.3б – Решающая цепь’ регулятора тока якоря

И спользуя данные по ЭПУ1М о напряжении датчика тока, и исходя из условия равенства параметром решающей цепи при сравнении двух датчиков тока получаем:

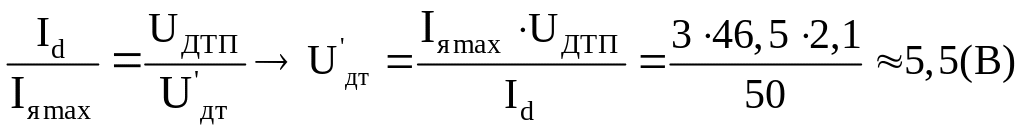(5.1.11)

(5.1.12)

5.2 Оптимизация контура эдс

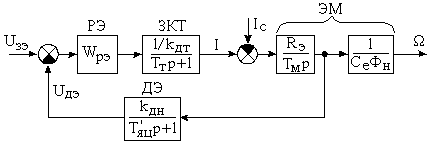
Рисунок 5.4 – Структурная схема контура ЭДС

РЭ – регулятор ЭДС;

ЗКТ – замкнутый контур тока;

ЭМ – электромеханическая часть двигателя;

ДЭ – датчик ЭДС.

Т_яц – постоянная времени якорной цепи двигателя, с которой снимается сигнал обратной связи по ЭДС.

В контуре имеются два звена с малыми постоянными времени, которые включены последовательно и поэтому могут быть преобразованы к одному звену с малой постоянной времени, равной их сумме:

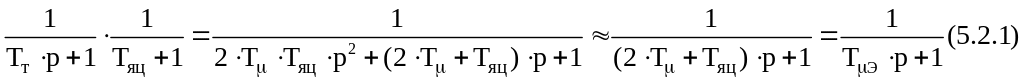Передаточная функция разомкнутого контура ЭДС, настроенного на модульный оптимум:

, (5.2.2)

о ткуда

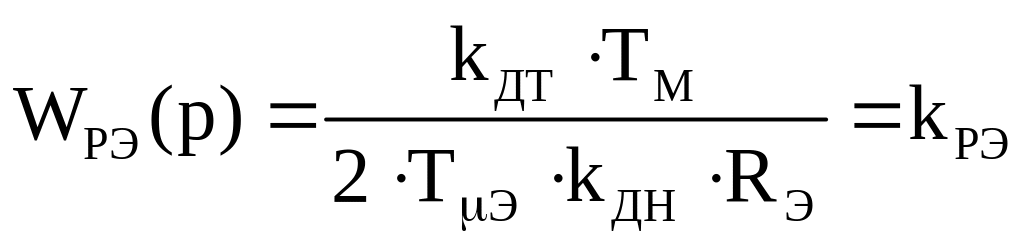. (5.2.3)

Получил пропорциональный регулятор (П-регулятор) ЭДС. С таким регулятором система будет астатичной по заданию (при отсутствии возмущающего воздействия) и статичной по возмущению.

Передаточная функция замкнутого контура ЭДС:

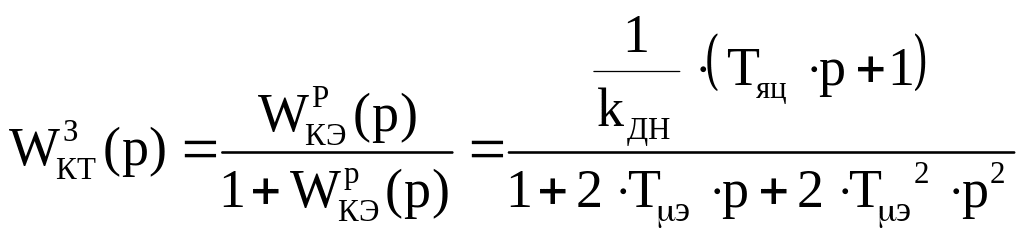. (5.2.4)

Таким образом, в замкнутой передаточной функции контура ЭДС присутствует форсирующее звено.

Из-за наличия инерционности в датчике ЭДС переходный процесс будет идти с большим перерегулированием. Для уменьшения перерегулирования на вход системы включаю фильтр с постоянной времени, равной инерционности датчика.

Передаточная функция фильтра .

(5.2.5)

Структурная схема замкнутого контура ЭДС имеет вид:

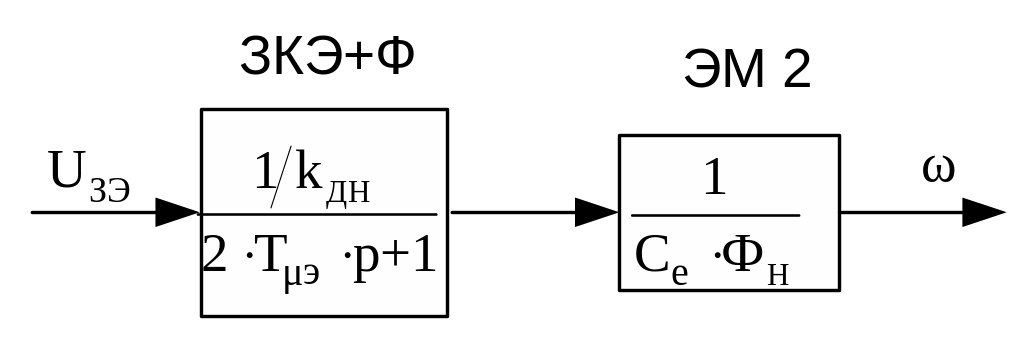
Рисунок 5.5 – Структурная схема замкнутого контура ЭДС

Р асчет параметров регулятора ЭДС с применением датчика напряжения

Рисунок 5.6 – Регулятор ЭДС

Коэффициент датчика напряжения:

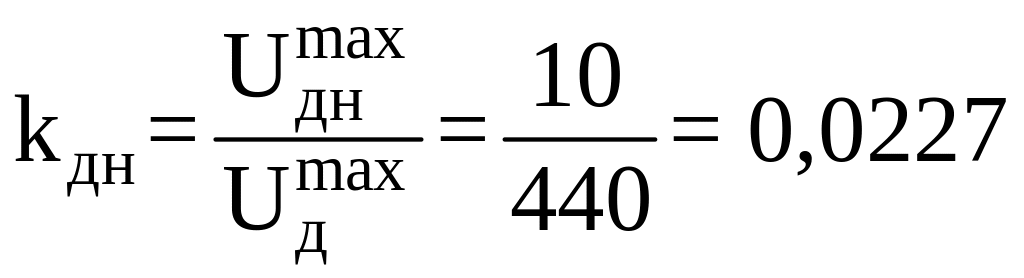. (5.2.6)

Коэффициент передачи регулятора ЭДС:

. (5.2.7)

Задаюсь ёмкостью в цепи датчика напряжения С_дн = 1 мкФ.

Сопротивление в цепи датчика напряжения:

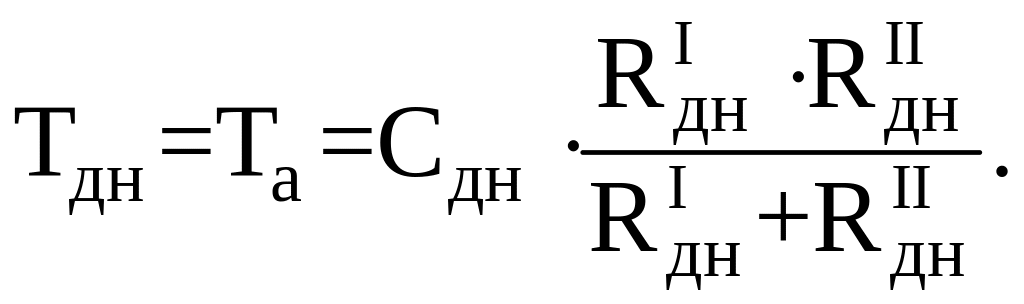(5.2.8)

где .

Если R^I_дн = R^II_дн = 0,5∙R_дн, то .

. (5.2.9)

Сопротивление в цепи обратной связи операционного усилителя регулятора напряжения:

R_оэ = k_рэR_дн = 2,1513210³ = 284 кОм. (5.2.10)

Сопротивление в цепи задания ЭДС нахожу из условий установившегося режима:

,I_зэ = I_дн,т.е. U_зэ^max = U_дн^max = 10 В,следовательноR_зэ = R_дн=132кОм.

Ё мкость фильтра в цепи определю из условия :

если R^I_зэ = R^II_зэ = 0,5∙R_зэ, то .

При R_зэ = R_дн С_ф = С_дн = 1 мкФ.

Сопротивление резистора токовой компенсации нахожу из условий режима стопорения двигателя: Е_д = 0 , U_дэ = 0.

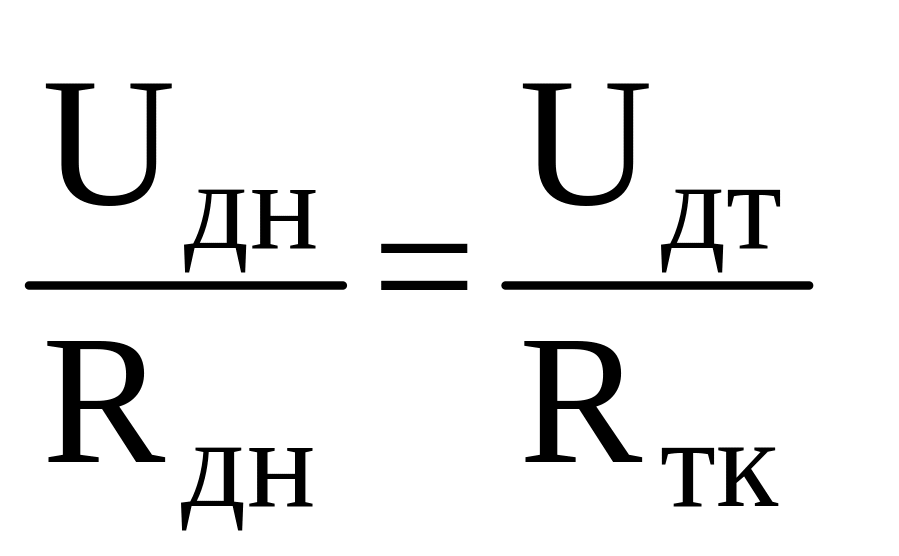. (5.2.11)

U_дт = Ik_дт, U_дн = U_дk_дн = I R_ak_дн,

. (5.2.12)

Сопротивления резисторов делителя . Считая k_пр = 1 и принимая R₃ = 1 кОм, выражаю R₄

. (5.2.13)

Ограничение выходного сигнала регулятора ЭДС осуществляется двумя встречно включенными стабилитронами VD1 и VD2 . Поскольку выходной сигнал регулятора ЭДС является сигналом задания на ток, то его ограничение приводит к ограничению тока двигателя на уровне максимально допустимого.

Падение напряжения на стабилитронах принимаем ΔU_ст = 1 В, максимально допустимое напряжение задания на ток U_зт^max = 10 В.

Тогда напряжение на стабилитронах будет равным:

U_VD1 = U_VD2 = U_зт^max – ΔU_ст = 10 – 1 = 9 В. (5.2.14)

5 .3 Оптимизация контура тока возбуждения

Так как привод однозонный, то оптимизацию контура тока возбуждения провожу для точки Ф_н.

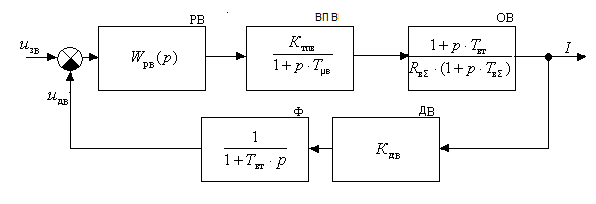
Рисунок 5.7 – Структурная схема контура тока возбуждения

РВ – регулятор тока возбуждения;

ВПВ – вентельный преобразователь цепи возбуждения;

ОВ – обмотка возбуждения;

ДВ – датчик тока возбуждении;

_{Ф – фильтр в цепи обратной связи предназначенный для осуществления обратной связи по току намагничивания.}

Найдём передаточную функцию регулятора тока возбуждения.

При настройке на модульный оптимум передаточная функция разомкнутого контура ЭДС имеет вид:

(5.3.1)

Передаточная функция регулятора тока возбуждения:

, (5.3.2)

где k_ртв – коэффициент регулятора тока;

- суммарное сопротивление якорной цепи, Ом.

Получил пропорционально-интегральный регулятор (ПИ-регулятор) контура тока возбуждения.

Р асчёт параметров регулятора тока возбуждения

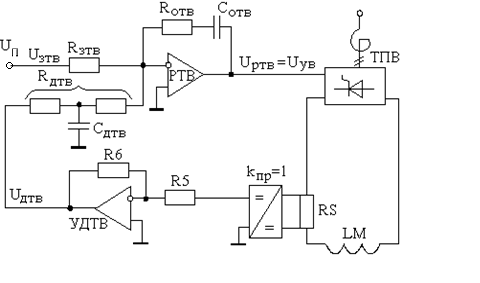
Рисунок 5.8а – Решающая цепь регулятора тока возбуждения

Коэффициент тиристорного преобразователя цепи возбуждения:

(5.3.3)

Определяю коэффициент регулятора тока возбуждения:

, (5.3.4)

где T_В∑ = T_в + T_вт = 0,071 + 0,0071 = 0,0781. (5.3.5)

Задаюсь величиной емкости конденсатора в обратной связи регулятора тока возбуждения:

C_отв = 1 мкФ.

Определяю сопротивление обратной связи регулятора тока возбуждения:

(5.3.6)

Определяю сопротивление датчика тока возбуждения:

. (5.3.7)

Ёмкость в цепи датчика тока возбуждения:

. (5.3.8)

С опротивление в цепи задатчика тока возбуждения:

(5.3.9)

_Пусть

Тогда (5.3.10)

Расчет для «П» регулятора тока возбуждения:

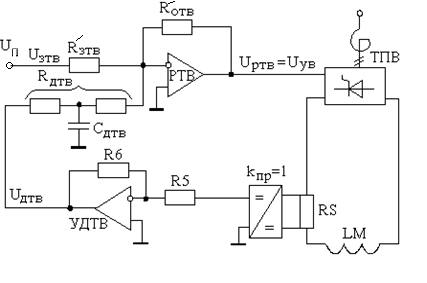
Рисунок 5.8б – Решающая цепь регулятора тока возбуждения

Определим реальный сигнал :

(5.3.11)

где . (5.3.12) Сопротивление резистора в цепи задатчика тока возбуждения:

(5.3.13)

6 РАСЧЕТ СКОРОСТНЫХ ХАРАКТЕРИСТИК И ИХ СТАТИЗМА В РЗОМКНУТОЙ И ЗАМКНУТОЙ СИСТЕМАХ ЭЛЕТРОПРИВОДА

Механические характеристики двигателя постоянного тока линейны, поэтому их построение произвожу по двум точкам, соответствующим режимам холостого хода и номинальной нагрузки.

Выражение для расчета механических характеристик имеет вид:

Ω = Ω₀ – Δ Ω, (6.1)

,А где Ω₀ –– угловая скорость идеального холостого хода.

. (6.2)

Падение скорости при номинальной нагрузке на естественной характеристике:

. (6.3)

Падение скорости при номинальной нагрузке в разомкнутой системе:

. (6.4)

Падение скорости при номинальной нагрузке в замкнутой системе

. (6.5)

где .

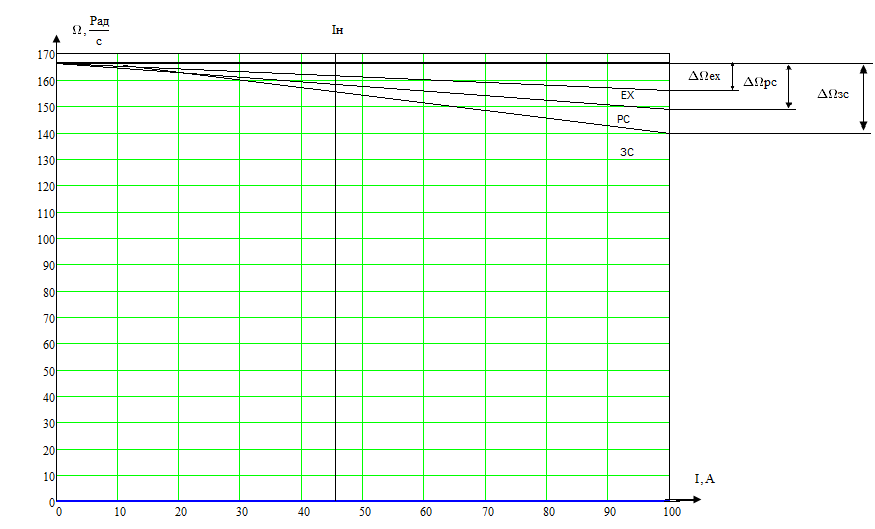
Рисунок 6.1 – Скоростные характеристики электропривода

Статизм естественной характеристики

. (6.6)

Статизм характеристики разомкнутой системы

. (6.7)

Статизм характеристики замкнутой системы

. (6.8)

Напряжение задания на скорость холостого хода _о

U_ЗС1 = _оk_днC_eФ_н = 166,120,0225210,212,610^-3 = 9,9 (В). (6.9)

Напряжение задания на скорость холостого хода  = 0,6∙_о на искусственной механической характеристике при пониженном напряжении

U_ЗС2 = 0,6_оk_днC_eФ_н = 0,6166,120,0225210,212,610^-3 = 5,94 (В). (6.10)

Из полученных графиков механических характеристик можно сказать, что естественная характеристика самая жесткая, характеристика разомкнутой системы более мягкая, чем естественная, а характеристика замкнутой системы – самая мягкая.

Большая мягкость механической характеристики – недостаток замкнутой системы, но в то же время система настроена на модульный оптимум и

п ереходные процессы будут идти с малым (4,3 %) перерегулированием и достаточно высоким (8,4Т_) быстродействием.

Но т.к. , то необходимо перейти к системе с ОС по ЭДС и ДЭ. И при определенном построении ДЭ, мы получим

(6.11)

7 РАСЧЕТ ДИНАМИЧЕСКОГО ПАДЕНИЯ СКОРОСТИ ДВИГАТЕЛЯ ПРИ НАБРОСЕ НОМИНАЛЬНОГО МОМЕНТА НАГРУЗКИ

Нахожу передаточную функцию замкнутого контура ЭДС по возмущению:

.

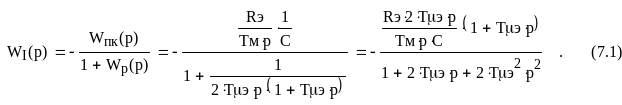Падение скорости в разомкнутой системе по Лапласу имеет вид:

. (7.2)

Следовательно, падение скорости в замкнутой системе в операторной форме запишется:

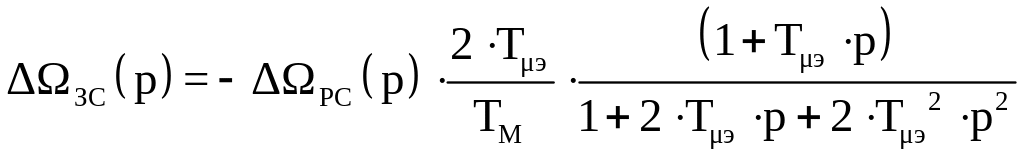. (7.3)

Переходя от изображения к оригиналу, падение скорости в замкнутой системе запишется:

. (7.4)

Следовательно выражение для кривой изменения падения скорости при набросе номинального момента нагрузки запишется следующим образом:

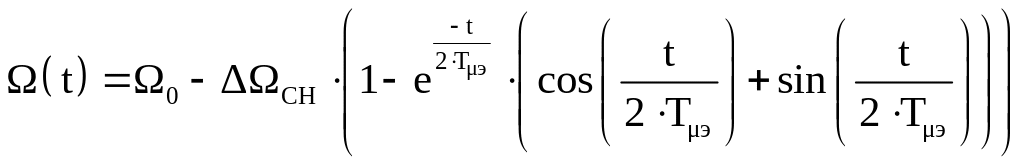, (7.5)

где . (7.6)

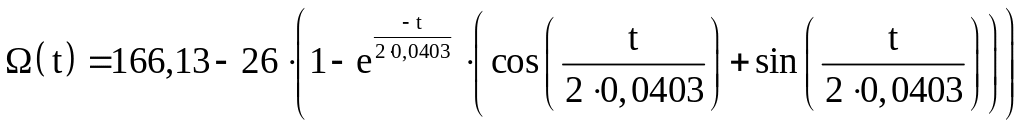(7.7)

Рисунок 7 – Кривая изменения падения скорости.

Переходный процесс идет с перерегулированием 4,3% и быстродействием 8,4Т_m.