Построчный алгоритм заполнения с затравкой
Как видно из предыдущего примера, стек может стать довольно большим. Еще один недостаток предыдущего алгоритма - стек зачастую содержит дублирующую или ненужную информацию. В построчном алгоритме заполнения с затравкой размер стека минимизируется за счет хранения только одного затравочного пиксела для любого непрерывного интервала на сканирующей строке. Непрерывный интервал - это группа примыкающих друг к другу пикселов (ограниченная уже заполненными или граничными пикселами). Мы для разработки алгоритма используем эвристический подход, однако также возможен и теоретический подход, основанный на теории графов.
Данный алгоритм применим к гранично-определенным областям. Гранично-определенная 4-связная область может быть как выпуклой, так и не выпуклой, а также может содержать дыры. В области, внешней и примыкающей к нашей гранично-определенной области, не должно быть пикселов с цветом, которым область или многоугольник заполняется. Схематично работу алгоритма можно разбить на четыре этапа.
Построчный алгоритм заполнения с затравкой
Затравочный пиксел на интервале извлекается из стека, содержащего затравочные пикселы.
Интервал с затравочным пикселом заполняется влево и вправо от затравки вдоль сканирующей строки до тех пор, пока не будет найдена граница.
В переменных Хлев и Хправ запоминаются крайний левый и крайний правый пикселы интервала.
В диапазоне Хлев <= x <= Xправ проверяются строки, расположенные непосредственно над и под текущей строкой. Определяется, есть ли на них еще не заполненные пикселы. Если такие пикселы есть (т. е. не все пикселы граничные, или уже заполненные), то в указанном диапазоне крайний правый пиксел в каждом интервале отмечается как затравочный и помещается в стек.
При инициализации алгоритма в стек помещается единственный затравочный пиксел, работа завершается при опустошении стека.
Теперь остается только один интереснй момент. После заполнения 4-связных полигональных подобластей с затравочными пикселами 5, 4 и 3 на рис. 2.16,е из стека извлекается пиксел, помеченный цифрой 2. Здесь мы обнаруживаем, что все пикселы на этой строке уже и на соседних строках (выше и ниже) уже заполнены. Таким образом, ни один пиксел в стек не помещается. Из стека извлекается пиксел 1 и строка обрабатывается, при этом вновь добавочных пикселов не появляется. Теперь стек пуст, многоугольник заполнен и работа алгоритма завершена.
По сравнению с алгоритмом из разд. 2.7 максимальная глубина стека в этом примере равна пяти.
Основы методов устранения ступенчатости
Чтобы эффективно бороться со ступенчатостью (лестничным эффектом), приводящей к искажениям в изображении, необходимо понимать причины, ее вызывающие. Основная причина появления лестничного эффекта заключается в том, что отрезки, ребра многоугольника, цветовые границы и т. д. имеют непрерывную природу, тогда как растровое устройство дискретно. Для представления отрезка, ребра многоугольника и т. д. на растровом устройстве необходимо начертить их в дискретных координатах, что может привести к удивительным результатам.
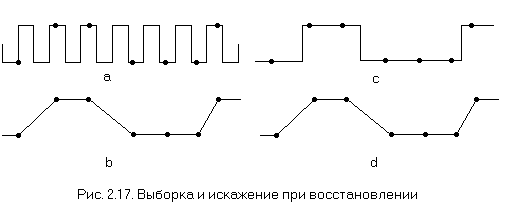
Рассмотрим, например, сигнал, изображенный на рис. 2.17,а. Второй сигнал более низкой частоты изображен на рис. 2.17,с. Если сделать выборки с одинаковой частотой из обоих сигналов (точки отмечены маленькими кружками), то восстановленные сигналы, показанные на рис. 2.17,b и d, идентичны. Рис. 2.17,d называется искажением выборки, показанной на рис. 2.17,b и, следовательно, сигнала на рис. 2.17,а. Для высокочастотного сигнала (рис. 2.17,а) выборка проведена с недостаточной частотой. Для предотвращения искажения следует проводить выборку сигнала с частотой, по крайней мере вдвое превышающей наибольшую частоту сигнала. Недостаточная выборка приводит к тому, что высокопериодичные изображения визуализируются неверно. Например, ограда забора или подъемные жалюзи могут выглядеть как несколько широких полос, а не как много отдельных, более узких полосок.
В основном существует два метода устранения искажений изображения такого рода. Первый связан с увеличением частоты выборки, что достигается с помощью увеличения разрешения растра. Таким образом, учитываются более мелкие детали. Однако существует определенное ограничение на способность растровых графических устройств с ЭЛТ выводить очень мелкие растры. Такое ограничение предполагает, что растр надо вычислять с более высоким разрешением, а изображать с более низким, используя усреднение некоторого типа для получения атрибутов пиксела с более низким разрешением.
Второй метод устранения искажений изображения состоит в том, чтобы трактовать пиксел не как точку, а как конечную область. В следующем разделе приводится эвристический метод этого подхода. Трактование пикселя как конечной области эквивалентно префильтрации изображения.