2. Теплопроводность при стационарном состоянии

При стационарном тепловом состоянии температура с тече­нием времени остается неизменной. В практике металлурги­ческой теплотехники подобные случаи передачи тепла теплопроводностью встречаются при передаче тепла через плоские стенки.

Однослойная стенка. Чтобы получить выражения, позво­ляющие определить распределение температур в стенке и количество передающегося через нее тепла, необходимо ре­шить дифференциальные уравнения теплопроводности со­вместно с краевыми условиями I рода. Применительно к этому случаю (рис. 33), когда тепло передается через стенку толщиной s=x₂— x₁ от поверхности с температурой Т₁ к поверхности с температурой Т₂, изменение температу­ры по толщине стенки описывается уравнением

T= ,

Рисунок 33 - Плоская однослойная стенка

а плотность теплового потока, проходящего через стенку, Вт/м²

q=

Следует заметить, что выражение представляет собой уравнение прямой линии, следовательно, распростра­нение температуры в однослойной плоской стенке при λ =const имеет прямолинейный характер. Если λ зависит от температуры, то распределение температуры имеет криво­линейный характер, причем кривая выгибается вверх, когда λ увеличивается с повышением температуры, и вниз, когда λ уменьшается с увеличением температуры.

Многослойная стенка. Рассмотрим плоскую стенку, со­стоящую из трех слоев

(рис. 34). Можно принять любое число слоев, причем каждый из них может обладать свои­ми физическими свойствами. Чтобы получить выражение, позволяющее определить количество тепла, проходящее через многослойную стенку, необходимо помнить, что для стационарного процесса плотность теплового потока, про­ходящего через каждый слой, одинакова, т. е. q₁= q₂=q₃=q

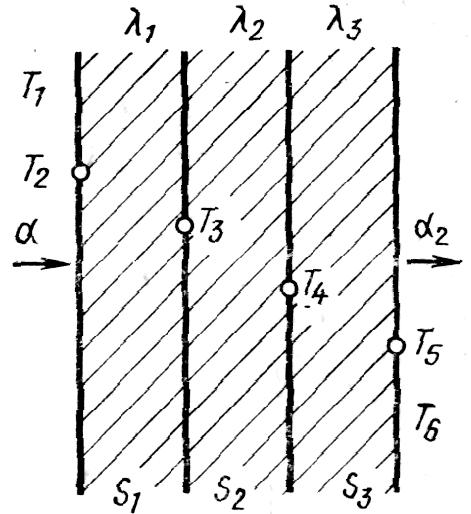
Рисунок 34 - Плоская трехслойная стенка

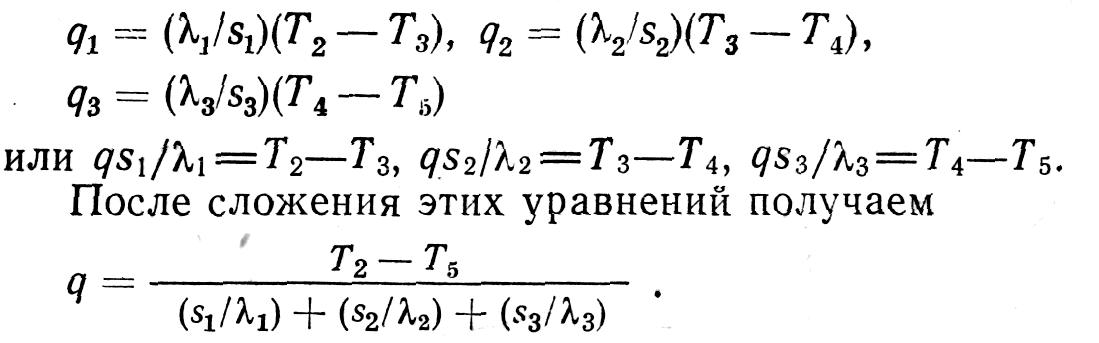
Как видно, знаменатель данного уравнения представля­ет собой сумму тепловых сопротивлений отдельных слоев.

Передача тепла от более нагретого газа к менее нагре­тому через плоскую стенку. На практике часто приходится определять количество тепла, которое требуется передать от одного газа к другому (или к жидкости) через стенку (многослойную или однослойную), т. е. решать задачу, по­добную изображенной на рис. 34.

Поскольку рассматривается стационарное тепловое со­стояние, постольку температуры теплоотдающего газа Т₁ и тепловоспринимающего газа Т₆, так же как и величины Т₂, Т₃, Т₄ и Т₅, остаются во времени неизменными. Соблюдение постоянства температуры окружающей среды — есть усло­вие, присущее граничным условиям III рода. Процесс теп­лообмена определяется в данном случае коэффициентами теплоотдачи α₁ и α₂.

Плотность теплового потока, который отдается более нагретым газом, может быть определена по выражению

q₁ = α₁ (T₁ — T₂).

Плотность теплового потока, который передается через стенку, была определена в предыдущем разделе:

q₂=

Плотность теплового потока, передаваемого- от стенки к менее нагретому газу:

q₃ = α₂ (Т₅ — Т₆).

При стационарном состоянии q₁ = q₂ = q₃ =q

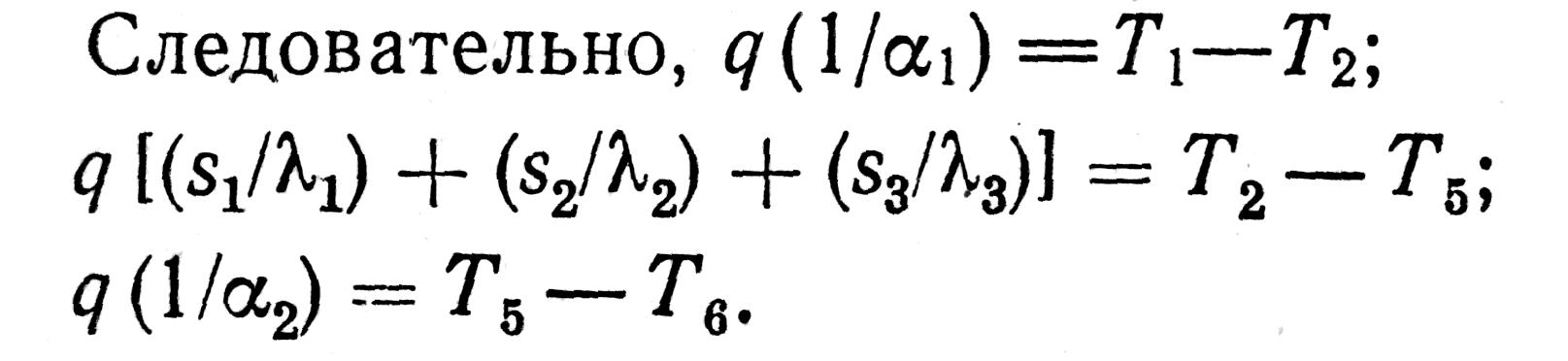
После сложения этих трех уравнений, получаем

Как указывалось выше, величина обратная коэффициен­ту теплоотдачи 1/ α₁ (или s/λ), выражает тепловое сопро­тивление. Следовательно, знаменатель уравнения представляет собой сумму тепловых сопротивлений различ­ных звеньев передачи тепла. Уравнение может быть записано в виде:

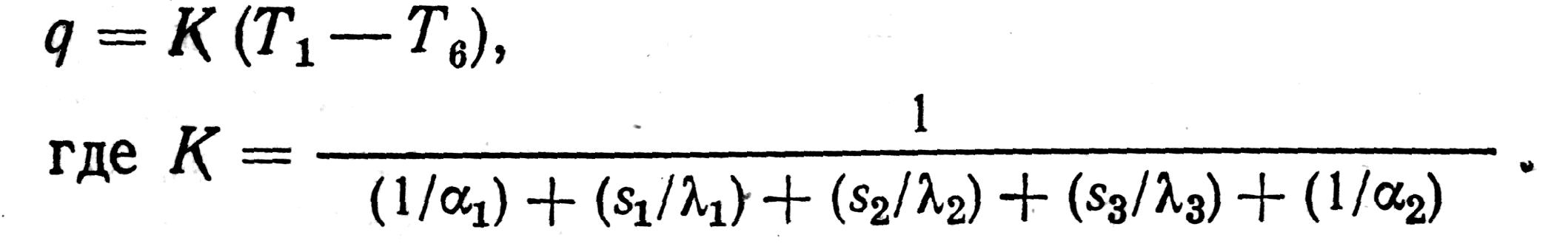
Величину К называют коэффициентом теплопередачи. Напомним, что разница между терминами «теплоотдача» и «теплопередача» заключается в том, что термин теплоотда­ча применим для какой-либо одной ступени передачи тепла, например от газа к стенке, от стенки к газу и т. п. Термин «теплопередача» применим для обозначения более сложно­го процесса передачи тепла, включающего в себя несколько ступеней этого процесса, например передачу тепла от газа к газу через стенку, где наблюдаются три ступени теплоперехода: от газа к стенке, через стенку и от стенки к друго­му газу. Подобным же образом можно объяснить различие между коэффициентом теплоотдачи α и коэффициентом теплопередачи К.

3. Теплопроводность при не стационарном состоянии

Основные решения. Как отмечалось выше, при нестаци­онарном состоянии с течением времени происходит измене­ние температуры тела, т.е. дТ/дτ≠О.

Подобное изменение температуры тела возможно, когда тело остывает или когда оно нагревается. На практике это широко распространенный процесс нагрева металла. Реше­ние дифференциального уравнения теплопроводности со­вместно с краевыми условиями представляет собой весьма сложную математическую задачу, поэтому остановимся лишь на решении при краевых условиях III рода, получив­шем наибольшее практическое распространение. На прак­тике часто встречаются печи, в которых нагрев металла происходит при неизменной температуре рабочего простран­ства. Некоторые печи с изменяющейся температурой по длине печи можно условно разделить на расчетные участки с приближенно неизменной температурой в пределах каж­дого участка и к каждому из них применить решения, полу­ченные при краевых условиях III рода.

Приведем без вывода окончательное решение дифферен­циального уравнения теплопроводности для бесконечной плиты при краевых условиях III рода, которое имеет сле­дующий вид:

где Т₀—температура печи (среды), К;

Т_НАЧ — температура металла в начальный момент нагрева, К;

а — коэффициент температуропроводности, м²/с;

τ — время нагрева (или ох­лаждения) тела, с;

S — расчетная толщина нагреваемого тела, м;

δ — величина, зависящая от αS/λ;

α — коэффици­ент теплоотдачи (от газа к металлу), Вт/(м²∙К);

х — рас­стояние от центра тела до той точки, для которой определя­ют температуру Т, м.

Анализируя уравнение (42), можно видеть, что темпера­тура нагрева металла Т зависит от трех безразмерных ком­плексов: критериев ατ/S², αS/ λ и x/S и что уравнение может быть заменено критериальным уравнением следую­щего вида:

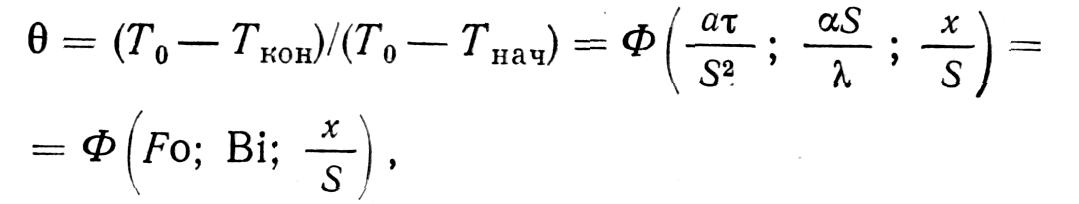
где Θ — безразмерный температурный критерий;

Т₀—тем­пература среды (печи);

Т_нач и Т_кон — температура нагрева­емого тела соответственно начальная и конечная.

В зависимости от условий решения уравнения Т_кон мо­жет представлять собой как конечную температуру поверх­ности тела (при x/S=1), так и конечную температуру в центре тела (при x/S = 0).

Безразмерный комплекс ατ/S² представляет собой из­вестный критерий Фурье, а безразмерный комплекс αS/λ — критерий Био.

Безразмерный геометрический симплекс x/S определяет собой местоположение точки в теле, для которой определя­ют температуру. Так, для центра нагреваемого тела х = 0 и x/S = 0, для поверхности тела x=S и x/S = l.

Таким образом, решая уравнение (3.2.3) для поверхности тела (x/S = 1), получаем температурный критерий