3. Сверхзвуковое движение газов

В металлургических печах в ряде случаев применяются такие устройства, в которых газ движется с весьма высокой скоростью, превышающей иногда скорость звука.

Согласно современным представлениям, скорость звука определяют формулой Лапласа, по которой

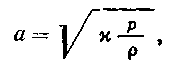
где χ — Ср/СV — коэффициент, равный отношению теплоем­кости среды при постоянном давлении к теплоемкости при постоянном объеме.

Применяя формулу Клапейрона (p/ρ=RT), получим

Из выражения следует, что скорость звука зависит только от температуры и физических свойств газа.

Скорость газа может быть мень­ше скорости звука, больше и равна ей. Если скорость движения газа станет равной местной скорости звука, то такая скорость газа w=a называется критической. Сечение потока, в котором достигается это равенство, называется критическим. Критическим называются также давление, плотность и температура в этом сечении.

Отношение скорости движения газа w к местной скорости звука а называется числом (кри­терием) Маха М. При М<1 поток дозвуковой, при М =1 звуковой и при М>1 сверхзвуковой.

Движение газа по трубе переменного сечения.

Посте­пенно сужающаяся по ходу газа труба называется конфузором, а постепенно расширяющаяся — диффузором. Соот­ношение между скоростью движения газов и сече­нием канала (трубы) переменного сечения описывается уравнением Гюгонио, которое в конечных разностях может быть представлено следующим образом:

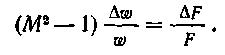
Величины Δω и ΔF представляют собой малые прираще­ния (изменения) соответственно скорости движения среды и сечения канала, по которому эта среда движется.

Из этого уравнения можно сделать следующие выводы:

1) если М<1, то знак Δω противоположен знаку ΔF.

Следовательно, при дозвуковом движении газа (как и не­сжимаемой жидкости) с возрастанием площади сечения трубы скорость движения уменьшается, и наоборот;

2. если М>1, то знак Δω одинаков со знаком ΔF. Сле­довательно, при сверхзвуковом движении в суживающейся трубе движение замедляется, а в расширяющейся трубе ускоряется. Это происходит в результате того, что при рас­ширении газа плотность его настолько сильно уменьшается,, что произведение pF уменьшается, несмотря на увеличение F. Это в свою очередь приводит к увеличению ω, посколь­ку pFw=const;

3. если М=1, то ΔF =0 и соответствующее сечение бу­дет критическим. Критическое сечение является минималь­ным, так как при подходе к нему дозвуковой поток замед­ляется, а сверхзвуковой ускоряется.

4. Простое сопло и сопло Лаваля

Простое сопло.

Большую роль в технике играют устрой­ства, обеспечивающие создание потока газа, истекающего с большой скоростью. Основным элементом таких устройств является сопло. При истечении газов через сопло происходит резкое изменение давления и, следовательно, объема. Поэтому уравнения движения и истечения, приве­денные выше для несжимаемого газа, здесь неприемлемы. Скорость истечения газов из сопла может быть дозву­ковой, равной скорости звука и сверхзвуковой.

П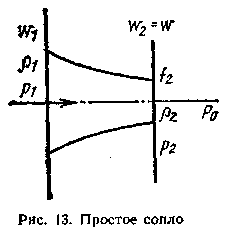 ри установившемся движении в каждом сечении соп­ла поток газов будет характеризоваться определенными ме­стными значениями скорости движения ω, давления Р, плотности р и температуры Т.

Если в данном сечении скорость движения газа ω рав­на скорости распространения звука, то скорость движения газа, давление и другие параметры, соответствующие этому условию, будут иметь критические значения ω_кр и Р_кр.

М

25

аксимальная скорость истечения газа из обычного (суживающегося) сопла может достигать только критического значения, но не выше, независимо от давления перед соплом. Критические параметры истечения из простого сопла могут быть определены из следующих выражений.

Критическая скорость истечения, м/с

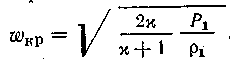
Критическое давление, Па

Критическая масса газа, кг/с

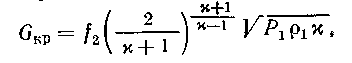
Коэффициент χ = 1,4 для двухатомных газов и χ=1,3 для сжатого пара.

Сопло Лаваля.

С

26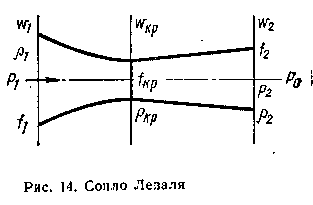

верхзвуковая скорость ω>ω_зв может быть получена в сопле, состоящем из суживающейся и рас­ширяющейся частей. Такое сопло называется соплом Лаваля по имени его создателя. Сопло Лаваля рассчитывают таким обра­зом, чтобы с корость в са­мом узком критическом се­чении его была критичес­кой, а в расширяющейся части превосходила звуко­вую, постепенно возрастая по мере приближения к выходному отверстию сопла. Если ско­рость в критическом сечении f_кр сопла будет меньше крити­ческой, то в расширяющейся части она будет уменьшаться, а не увеличиваться, т.е. будет изменяться так же, как и в обычном сопле.

Характеристики истечения из сопла Лаваля могут быть определены из следующих выражений:

к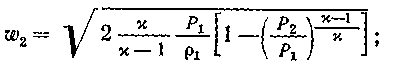 ритическая скорость, м/с

критическая масса, кг/с

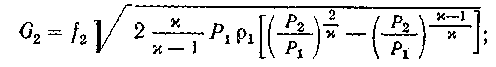
площадь сечения, м²

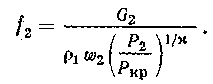
Сопла Лаваля широко применяются при создании кис­лородных и газокислородных фурм для конвертеров, мар­теновских и двухванных печей.