5.5 УточнеНие способа определения длительностИ воздействия колёсной нагрузки на поверхностЬ дорожной одежды

Горячев М.Г., Горячева Е.В. (МАДИ, г. Москва, РФ)

Приведён подробный вывод нового выражения для вычисления продолжительности воздействия на поверхность дорожной одежды единичной колёсной автотранспортной нагрузки, учитывающей все основные параметры взаимодействия. Предложенный способ может быть использован для определения суммарного времени воздействия в различных моделях расчёта дорожных одежд и оценки их работоспособности.

The author gives the detailed conclusion of a new expression for calculating the duration of the exposure to the pavement by the single wheel loading. The expression considers all main parameters of interacting. The offered method can be used to determine the total exposure time in various models of calculation of pavements and to estimate its working capacity.

Суммарное время нагружения дорожной конструкции произвольной подвижной нагрузкой складывается из произведений однократного времени приложения этой нагрузки t_Ц на количество приложений за учитываемые временные отрезки

, с, (1)

где i – отрезок времени с интенсивностью нагружения N_i;

z – количество учитываемых временных отрезков.

В упрощённой трактовке длительность нагружения устанавливают по соотношению линейного параметра штампа и скорости его перемещения по траектории этого параметра. За направление обычно принимают продольное движение по проезжей части. За параметр штампа – диаметр, по которому вычисленная площадь отпечатка равна площади фактического контура отпечатка. Фактическим контуром является эллиптическая форма. Искривлением поверхности, т.е. вогнутой частью чаши прогиба, пренебрегают, а гибкий штамп подменяют квазижёстким. Таким образом, процесс описывается кинематически при изложенных упрощениях

, с, (2)

где D – диаметр штампа, м;

V – скорость перемещения штампа, м/с.

Хорошо известно [1, 2, 3], что область напряжённого состояния при качении гибкого штампа выходит за пределы его отпечатка – происходит формирование чаши прогиба в нагружаемом полупространстве. А.В. Смирнов и А.С. Александров, разделив процесс воздействия реальной нагрузки на три стадии [2] и опираясь на гипотезу Н.Я. Хархуты о допустимости замены продолжительности напряжённого состояния на его эквивалент, развили зависимость (2)

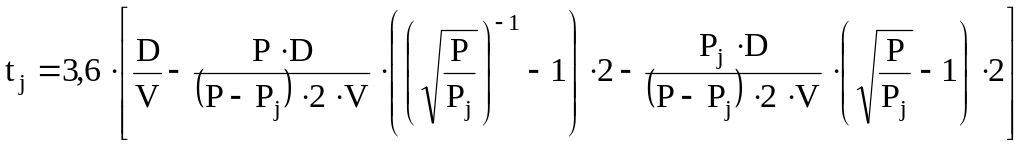, с (3)

где Р – давление в основании жёсткого штампа, МПа;

P_j – предельные напряжения свойства материала (упругости, вязкости, текучести и т.д.), МПа.

Основным достоинством зависимости (3) следует считать достаточно успешную попытку выполнить учёт свойств материалов дорожной конструкции. Для практических расчётов это достижение реализовать проблематично. В этом решении отсутствует величина нагрузки и не учитываются прочность и жёсткость нагружаемого полупространства. Кроме того, колесо автомобиля представляет собой гибкий штамп с эллиптическим контуром, ориентированным на проезжей части в зависимости от конструкции штампа: при односкатном профиле большая ось эллипса совпадает с направлением движения, при двускатном – перпендикулярна направлению движения.

Решение задачи по глубине потребует оперирования гипотетически задаваемым углом распределения давлений в полупространстве, что в свою очередь основано на нескольких осреднённых входных физико-механических показателях.

С.В. Лугов предложил определять длительность нагружения по глубине, исходя из приведения объёмной эпюры напряжений в дорожной одежде к эквивалентной, подобной по форме цилиндрической и с одной из сторон равной продольному размеру чаши прогиба [3]

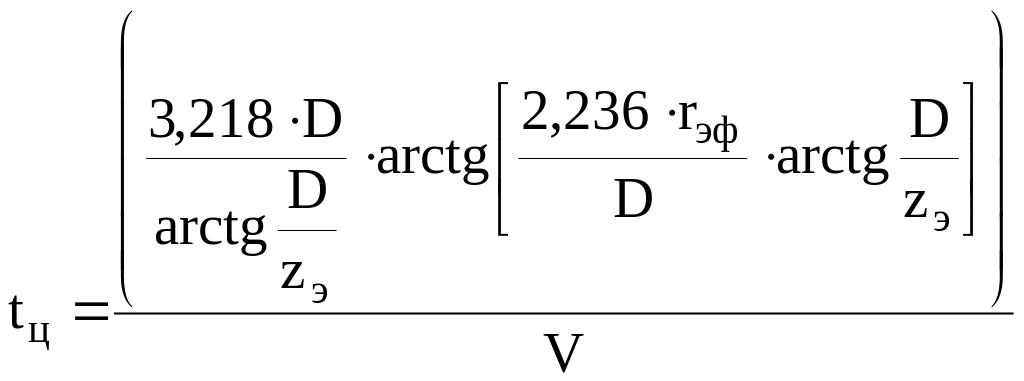, с, (4)

где z_Э – толщина эквивалентного слоя слоёв дорожной одежды, м;

r_ЭФ – так называемое «эффективное расстояние» от центра приложения штампа до края чаши прогиба по траектории перемещения штампа; очевидно, удвоенное значение r_ЭФ равно продольному размеру чаши прогиба, м.

Зависимость (4) позволяет устанавливать длительность напряжённого воздействия по толщине конструкции, но обладает теми же недостатками, что и функция (3) и не даёт решения на поверхности дорожной одежды.

Устранение слабых сторон известных решений произведём математическим описанием гибкого контакта эллиптического очертания. Геометрически задача сводится к следующему.

Запишем площадь эллипса для плоской задачи

, м². (5)

где Q – колёсная нагрузка, кН;

Р – давление в области контакта протектора с поверхностью дорожной одежды с учётом жёсткости шины, МПа.

Следовательно, большая ось эллипса на горизонтальной плоскости при отсутствии прогиба

, м. (6)

Планиметрическая ширина отпечатка составит (рисунок 1)

, м, (7)

где b_ш – ширина беговой дорожки шины по её техническим характеристикам – ширина части протектора, непосредственно контактирующая с покрытием, м;

К_ш – коэффициент увеличения ширины беговой дорожки; в режиме качения в среднем К_ш=1,05…1,07.

, м. (8)

Образование чаши прогиба приводит к некоторому искажению параметров эллипса (рисунок 1).

Рисунок 1 - Схема к описанию геометрических параметров длительности воздействия колеса на поверхность дорожной одежды: А – в направлении движения; В – вдоль направления движения

Длительность проезда в пределах плоской кривой контакта колеса с покрытием на схеме

, с. (9)

В рассматриваемой схеме по длине

, м; (10)

по ширине

, м. (11)

Для определения длины дуги качения – обозначим её , в пределах которой проводим учёт напряжённого состояния, применим формулу Гюйгенса

, м, (12)

Классически, обратно пропорциональная связь между упругим прогибом одежды по приведённому к круговой поверхности отпечатку протектора и общим модулем упругости Е_общ описывается известной зависимостью

, м, (13)

где  – осреднённый коэффициент Пуассона конструкции.

Поскольку , м, (14)

то

, м. (15)

С учётом выражения (14) разовьём формулу (11)

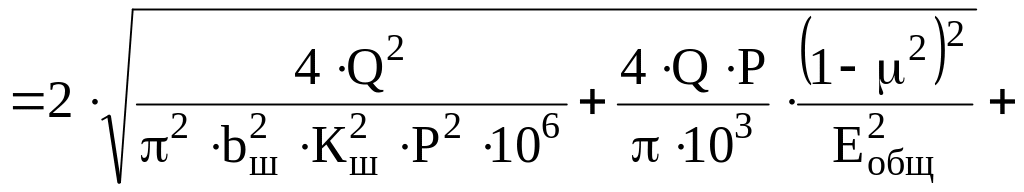(16)

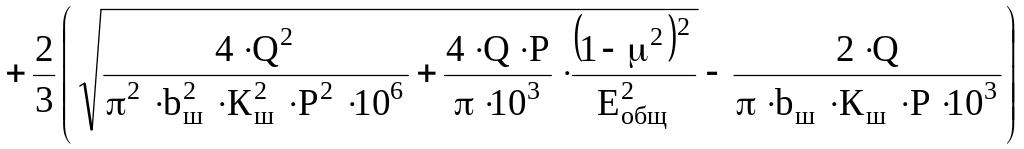, м.

Сократим, объединяя дроби с однокоренными составляющими

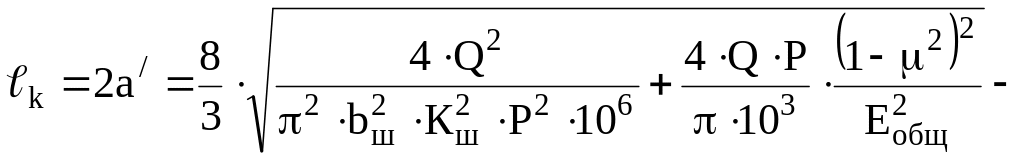
, м. (17)

Аналогично для ширины плоскости качения

, м. (18)

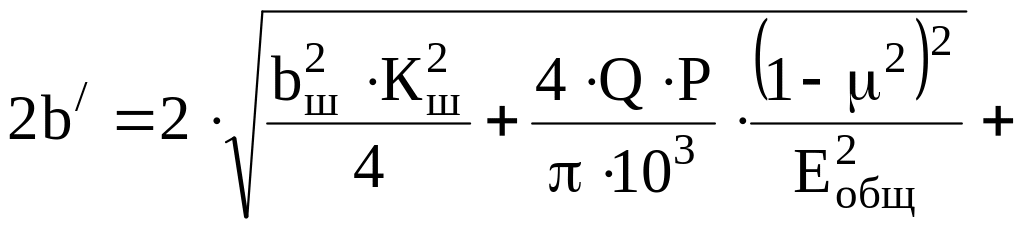
, м. (19)

Упрощая, получим

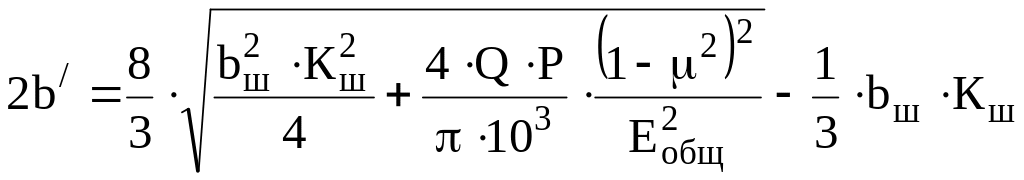, м. (20)

Такое решение будет справедливо для конструкции гибкого штампа (колеса) со следом продольно вытянутого эллипса. Если же гибкий штамп смоделирован с шириной профиля больше длины, ориентирование эллипса прямоугольно изменится, а длина плоской кривой бега будет соответствовать искривлённой по чаше прогиба малой оси эллипса.

Теперь запишем зависимость для длительности нагружения в строгой форме

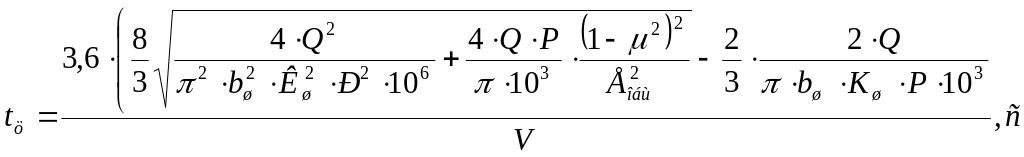(21)

Простейшие расчёты свидетельствуют, что вполне допустимо пренебречь учётом деформации одежды на расчётную длительность её нагружения в предложенной схеме через сопоставительную оценку абсолютных значений а и а^/, b и b^/. Самое существенное относительное различие составило всего 0,05%.

Тогда без учёта деформации одежды длительность контакта штампа

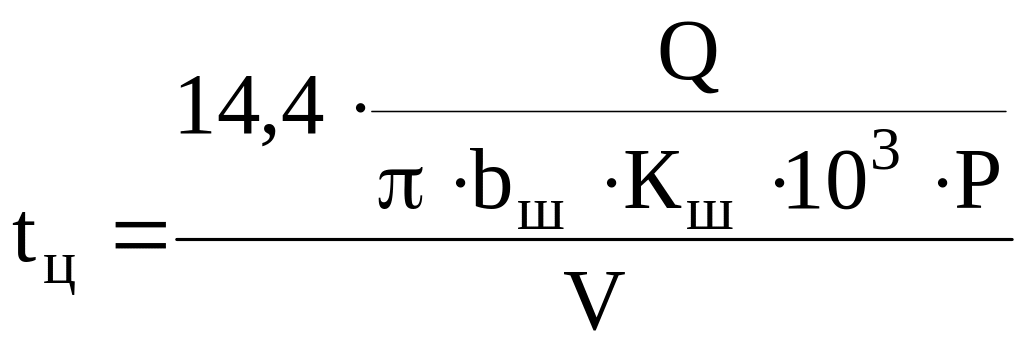, с. (22)

В выведенных выражениях (20) и (21) нашли отражение все главные параметры взаимодействия колеса с дорожной одеждой, которые к тому же являются определяющими при проектировании дорожных одежд. При этом не потребуется прямое испытание сложно поддающихся точному описанию и определению неоднородных показателей физико-механический свойств материалов и макетов одежды.

Если поставлена задача уточнения необходимого для учёта времени воздействия циклической нагрузки с позиции оценки характера деформационного процесса (или сопротивлений структуры по [2]), то можно легко синтезировать оба метода, заменяя в формуле (3) диаметр D на числитель дроби из (21). Тогда получим

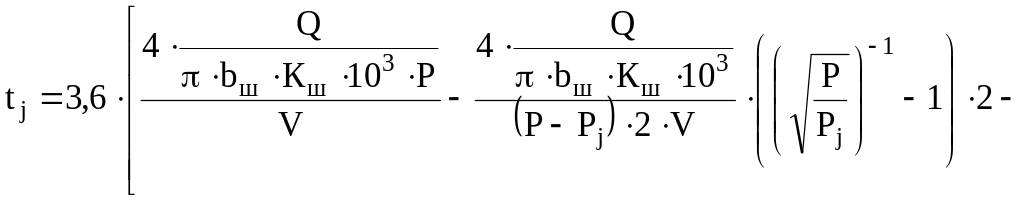
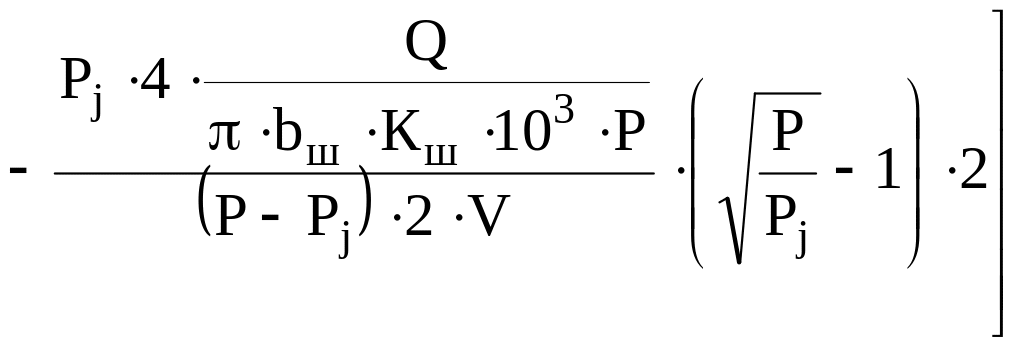, с. (23)

Размеры чаши прогиба намного превосходят контур отпечатка штампа. При теоретическом обосновании параметров установок динамического нагружения д-р техн. наук Ю.М. Яковлев [1], учитывая совместные исследования с канд. техн. наук В.А. Лейваком [4], находил длительность действия колеса автомобиля исходя из продольного размера чаши прогиба L_ПР

, с. (24)

Последовательное перемещение штампа в пределах чаши прогиба сопровождается изменениями значений напряжения сжатия, поэтому общее время проезда необходимо заменять на его эквивалент

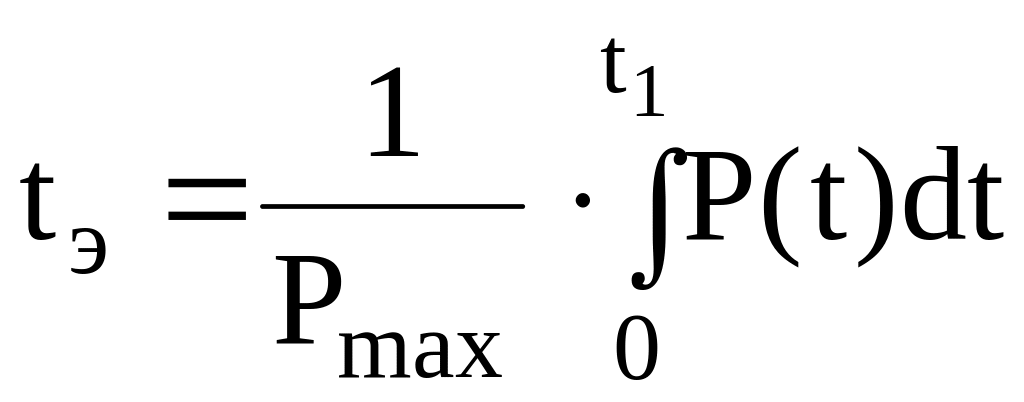, с, (25)

где P_max – максимальная удельная нагрузка (максимальное контактное давление) на пределе нарастания напряжения, МПа;

t₁ – время завершения нарастания усилия, с.

Учитывая синусоидальный характер нарастании усилия при малой скоро­сти нагружения (при отсутствии выраженного динамического эффекта), дока­занный исследованиями Н.Я. Хархуты, проф. Ю.М. Яковлев строго получил коэффициент пропорциональности между t_Ц (формула 23) и t_Э

, с. (26)

Соотношение (25) приводит к очень высокой сходимости с результатами оценки прогибов нежёстких дорожных одежд по Б.С. Радовскому и В.И. Кот­ляру. Анализируя экспериментальные данные о параметрах чаши прогиба и выражение (25), можно вывести хорошо корреспондирующую связь между длительностью воздействия эллиптического штампа в направлении движения и полным эквивалентным временем однократного приложения нагрузки на по­верхности дорожной одежды

, с. (27)

Теперь с учётом участков перехода (зон нарастания и затухания давле­ний) к месту приложения штампа выражение (21) предстаёт в следующем виде

, с. (28)

Из строительной механики (труды Г. Герца и отечественных специали­стов) известно, что эпюра напряжений по площадке соприкосновения шарооб­разной фигуры с плоскостью имеет форму полуэллипсоида с максимальным напряжением под центром штампа, равным

, МПа. (29)

Интеграл полуэллипсоида эпюры напряжений следует из канонического уравнения эллипса в декартовой системе координат

, (30)

где а – полуось в направлении качения колеса;

b – полуось, равная по величине напряжению по центру контакта; b=Р_max.

Тогда

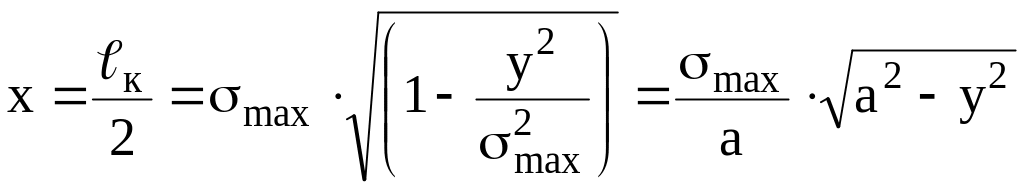. (31)

Выполним интегрирование на отрезке от края штампа до его центра с удво­ением для достижения результата по всей длине дуги качения, заменяя σ_max на (28)

. (32)

Чтобы оперировать в формуле (27) постоянным на длине дуги качения расчётным контактным давлением, приведём эпюру напряжений к эквиваленту, в котором каждая точка контакта на дуге качения испытывает давление, равное Р – рисунок 2. Площадь эквивалентной (прямоугольной) эпюры напряжений

, (33)

где – эквивалентная длина дуги качения, м.

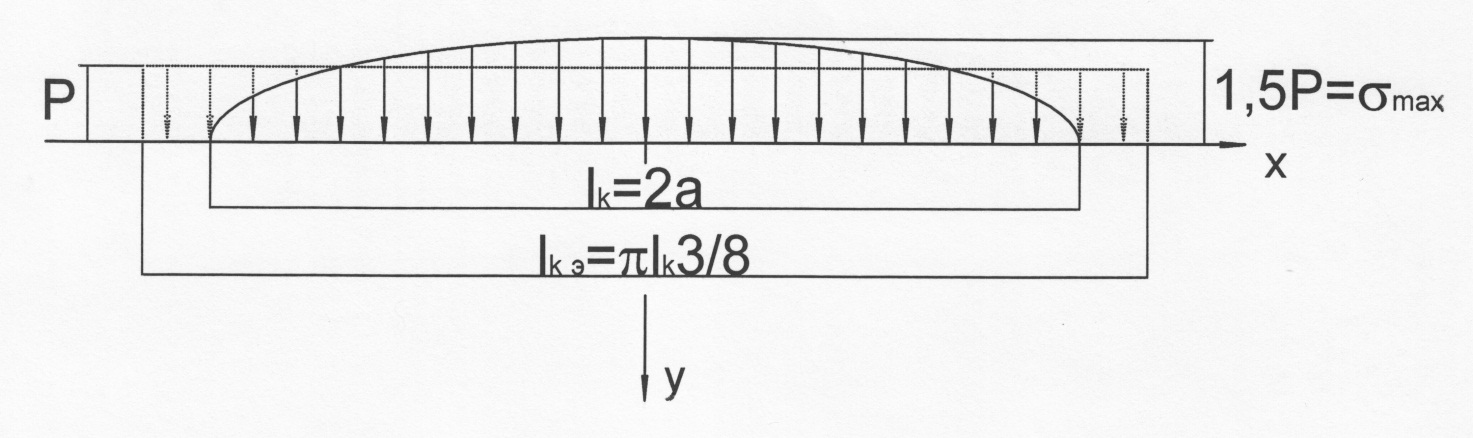
Рисунок 2 - Схема приведения фактической эпюры напряжений под колёсным штампом

к эквива­лентной равнонапряжённой эпюре

Приравняв (31) и (32), получим

. (34)

Такой результат означает, что эквивалентно нагруженная площадка вы­ходит за пределы фактического контура соприкосновения колёсного штампа в раз, что увеличивает длительность нагружения почти на 18%.

Внесём уточнения в формулу (27)

, с. (35)

Заключение

Предложено уточнённое кинематическое выражение для вычисления длительности воздействия динамического усилия на дорожную одежду через эквивалентное время, учитывающее разнонапряжённый характер нагружения по контуру фактического очертания. Контактное давление от подвижной транспортной нагрузки передаётся на поверхность дорожной одежды по эллиптическому контуру. Формируемая при этом эпюра напряжений имеет полуэллиптическую конфигурацию с градиентом в направлении движения от нуля на границах чаши прогиба и экстремумом непосредственно под колёсным штампом.

Литература

1 Яковлев, Ю.М. Оценка и обеспечение прочности дорожных одежд нежёсткого типа в процессе эксплуатации: Дис. ...д-ра техн. наук, – М., 1985. – 435с.

2 Смирнов, А.В. Механика дорожных конструкций / А.В. Смирнов, А.С. Александров. Учебное пособие // СибАДИ, 2009 – Омск. – 211с.

3 Лугов, С.В. Основные положения методики расчёта глубины колеи на до­рожных одеждах с асфальтобетонным покрытием: Дисс. ...канд. техн. наук. – М., 2004. – 267с.

4 Лейвак, В.А. Исследование параметров, характеризующих прочность нежёстких дорожных одежд при их испытаниях динамической нагрузкой: Дисс. ...канд. техн. наук. – М., 1976. – 156с.