5.2 Применение методов оптимизации при проектировании автомобильных дорог

Ахраменко Г.В. (БелГУТ, г. Гомель, Беларусь)

Рассматриваются методы оптимизации проектных решений при проектировании автомобильных дорог. Приведены примеры определения оптимальной глубины выемки с помощью чисел Фибоначчи и выбора направления трассы с использованием множества Парето на локальных участках.

Discusses methods for optimizing the design decisions in the design of highways. Examples are given to determine the optimal depth of the recess with the Fibonacci numbers and select the direction of the route using the Pareto set in local areas.

Как известно, под оптимизацией понимается процесс выбора наилучшего варианта из всех возможных. В процессе решения задачи оптимизации необходимо найти оптимальное значение проектных параметров, определяющих данную задачу. Ситуация, в которой необходимо принимать решения, типична и для процесса разработки проектов новых автомобильных дорог.

Главная задача, возникающая перед разработчиком проекта автомобильной дороги, состоит в том, чтобы принять обоснованные решения по структуре элементов системы и их параметрам [1]. Эта задача может быть сформулирована следующим образом: разработать проект автомобильной дороги с такой структурой элементов и их параметрами, чтобы обеспечить заданные размеры перевозок (параметры цели) при минимальных затратах. В условиях, когда затраты на строительство автомобильной дороги регламентированы, возможна постановка другой задачи проектирования: разработать проект автомобильной дороги с такой структурой элементов, чтобы обеспечить максимальные размеры перевозок при заданных затратах. В общем случае оптимизация проектных задач сводится к выявлению показателя (критерия оптимальности), по величине которого можно производить оценку сравниваемых вариантов и к выявлению условий, при которых этот показатель принимает искомое, наиболее рациональное значение.

В зависимости от характера решаемых проектных задач, критерий оптимальности может быть выражен в соответствующих для этой задачи измерителях (объемах работ, трудоемкости, стоимостных показателях и т. п.). В большинстве случаев при проектировании возникает необходимость выявлять эффективность проектных решений как в строительном, так и в эксплуатационном отношениях. Для оптимизации такого рода задач в проектной практике применяются стоимостные показатели, выраженные обычно суммой приведенных строительных и эксплуатационных затрат.

Величина критерия зависит от значения переменных, отыскание которых осуществляется при решении той или иной проектной задачи. Эти переменные являются независимыми, но так как их величина или шаг изменения для достижения того или иного значения критерия может назначаться проектировщиком, то их можно считать управляемыми. Если функциональная зависимость между критерием и управляемыми переменными полностью выявлена, то при дискретном изменении этих переменных задачи по отысканию оптимума могут быть решены с использованием линейного и динамического программирования. Однако в большинстве случаев при проектировании автомобильных дорог зависимость между критерием и управляемой переменной известна не полностью и процесс нахождения оптимума связан с необходимостью производства эксперимента (разработкой вариантов проектных решений).

Стратегия поиска, т. е. набор правил, по которым осуществляется назначение числа и последовательность производства экспериментов для выявления оптимального решения, где заранее назначаются и выполняются все без исключения эксперименты, является пассивной. Стратегия, в которой все последующие эксперименты (их число и последовательность выполнения) зависят от результатов предшествующих, является последовательной или направленного поиска [2].

При решении задач с применением стратегии пассивного поиска все эксперименты осуществляются до или же в процессе выявления оптимального решения, но при условии, что все сопоставляемые эксперименты без какого-либо сокращения должны быть выполнены и рассмотрены. Выявление оптимального варианта с использованием стратегии пассивного поиска может быть осуществлено простым или неупорядоченным перебором, или же производя этот перебор в определенном порядке, т. е. упорядоченным перебором, который наиболее целесообразен при наличии большого числа различных вариантов (экспериментов). Такой перебор может быть осуществлен с применением методов решения транспортных задач, нахождения «кратчайшего» пути в графе, на основании применения основных принципов динамического программирования и т. п. [3, 4].

Все методы решения задач с применением стратегии последовательного или направленного поиска сводятся к установлению первоначального интервала неопределенности, проведению некоторого числа опытов в пределах этого интервала, сопоставлению результатов этих опытов, и на основании этого, к выявлению нового (сокращенного) интервала неопределенности, в пределах которого осуществляется новая группа опытов и производится дальнейшее уменьшение интервала неопределенности, и так до тех пор, пока не будет выявлено окончательное оптимальное решение.

Для определения необходимой последовательности производства опытов (экспериментов) в математике рекомендуются различные методы: метод дихотомии, метод Фибоначчи, «золотого сечения», поиск по дискретным точкам. В данной статье рассматривается стратегия последовательного поиска с применением метода Фибоначчи, который может быть с достаточной эффективностью применен при решении ряда проектных задач. Этот метод основан на производстве экспериментов для последовательного уменьшения интервала неопределенности в порядке, соответствующем числам Фибоначчи [5].

Числа Фибоначчи образованы таким путем, что каждое последующее число (кроме нулевого и первого по порядку расчета) равно сумме двух предшествующих. Если обозначить Число Фибоначчи F_n, где n соответствует порядковому номеру числа, то

F₀ = F₁ = 1; F_n = F_{n – 1} + F_{n – 2} ; n = 2, 3, 4, 5 (1)

Для n от нуля до 10 эти числа приведены в таблице 1.

Таблица 1 – Числа Фибоначчи

n	0	1	2	3	4	5	6	7	8	9	10
Fn	1	1	2	3	5	8	13	21	34	55	89

Применение этих чисел позволяет существенно сократить диапазон поиска, или интервал неопределенности. Так, если для выявления какого-либо оптимального значения при стратегии пассивного поиска необходимо осуществить 89 экспериментов, или, иначе, известно, что это оптимальное значение находится в интервале неопределенности, соответствующем 89 экспериментам, то это соответствует числу Фибоначчи F₁₀ и при последовательном поиске в направлении к F₁ найти это оптимальное значение можно, осуществив всего лишь 10 экспериментов.

Допустим, что решается задача по определению оптимальной глубины выемки при пересечении перевала в пределах до 21 м. Если глубина выемки определяется с точностью до 1,0 м, то в этом случае первоначальный интервал неопределенности можно считать равным 21 и при стратегии пассивного поиска следовало бы осуществить 21 эксперимент (вариант проектировок). В качестве критерия можно принять минимальные приведенные расходы, которые определяются по формуле

(1)

или

(2)

где E_н – нормативный коэффициент эффективности; K – капитальные вложения, тыс. руб.; С – текущие расходы, тыс. руб./год; Т_н – нормативный срок окупаемости, лет [3].

Цифра 21 соответствует числу Фибоначчи F₇. Учитывая, что это число получено как F₇ = F₆ + F₅ при F₆ = 13 и F₅ = 8, то при направленном поиске, используя числа Фибоначчи, намечается первая группа экспериментов, соответствующая проектировке выемки при глубине 13 и 8 м (два эксперимента). При этих глубинах выемки определяются критерии S₁₃ и S₈. Исходя из унимодальности функции, можно предположить, что если S₈ > S₁₃, то искомый минимум S расположен правее точки 8 и может находиться в интервале между точками 8 и 13 или 13 и 21, но не может быть в интервале 1–8 (рисунок 1). В этом случае интервал 1–8 отпадает. Наоборот, если S₈ < S₁₃, то отпадает интервал от точки 13 до 21. Таким образом, после двух экспериментов интервал неопределенности сокращается до 13.

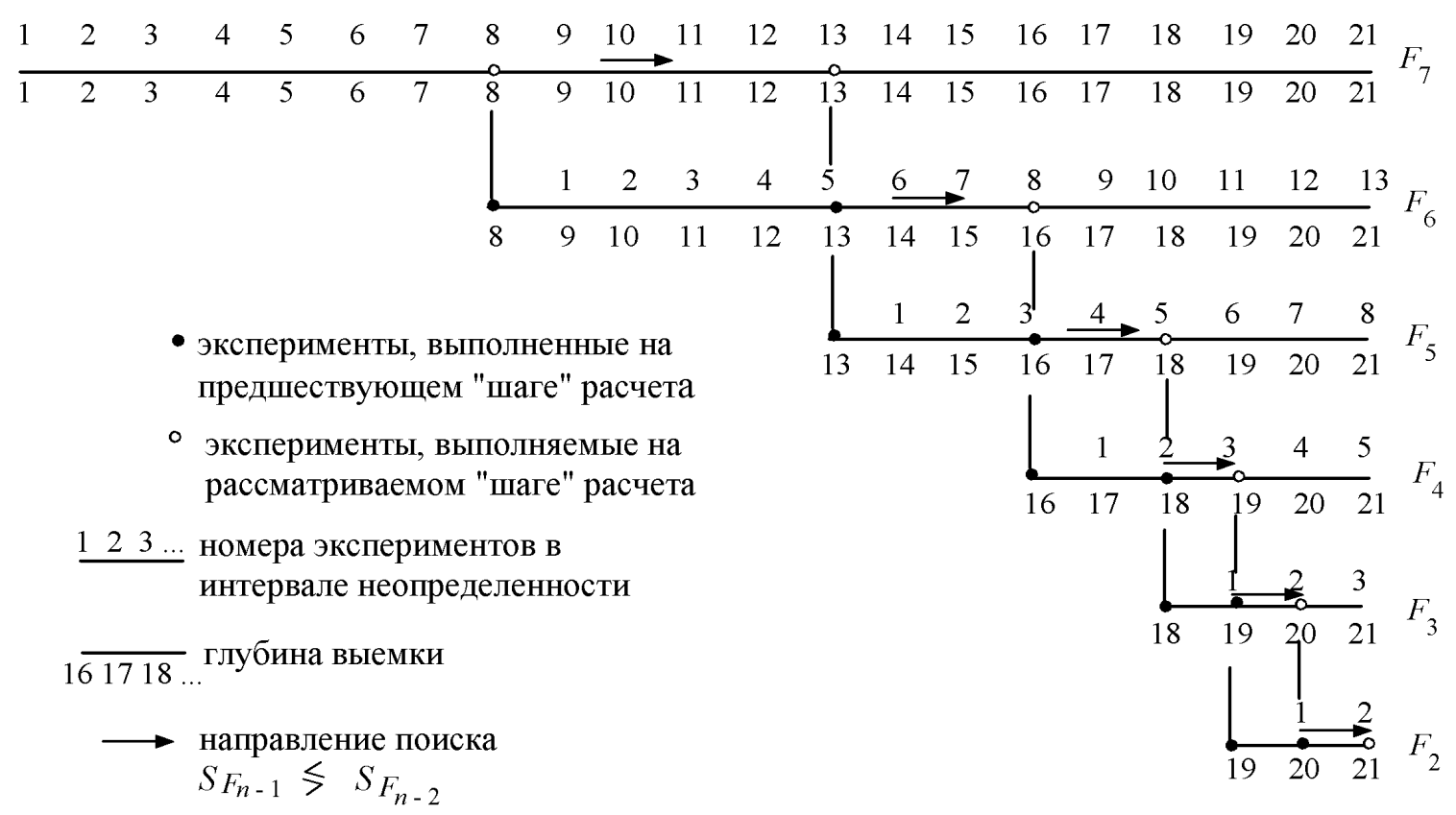
Рисунок 1 – Последовательность поиска при помощи чисел Фибоначчи

Допустим, что в рассматриваемом случае S₈ > S₁₃, перенесем начало координат в точку 8. В связи с тем, что новый интервал неопределенности, равный 13, соответствует числу Фибоначчи F₆, а F₆ = F₅ + F₄ при F₅ = 8 и F₄ =5, то следующие эксперименты назначаются в точках 5 и 8, что соответствует глубинам выемки 13 и 16 м (см. рисунок 1). Если и в этом случае S₁₃ > S₁₆, то экстремум находится правее точки 13 и интервал до точки 13 (в старой нумерации) отпадает.

Новый интервал неопределенности (21 – 13 = 8) соответствует F₅ = 8, в котором дополнительный эксперимент назначается при глубине выемки 18 м. При S₁₆ > S₁₈ выявляется новый интервал неопределенности, соответствующий F₄ = 5. И так продолжается до тех пор, пока критерий нового эксперимента не станет больше предшествующего. С использованием чисел Фибоначчи общее число вариантов сократилось с 21 до 7. Приведенный на рисунке 1 случай соответствует выявлению минимума критерия при наибольшей глубине выемки (крайний случай). Следует учесть, что применение метода Фибоначчи требует всегда установления первоначального интервала неопределенности, совпадающего с каким-либо числом Фибоначчи. При решении большинства проектных задач установить такой интервал неопределенности можно выбором соответствующего масштаба или точности расчета.

Рассмотренный метод предполагает наличие одного экстремума (минимум приведенных затрат), и является по своей сути задачей унимодальной. В большинстве случаев задачи, связанные с оптимизацией решений при проектировании автомобильных дорог, являются многокритериальными. При решении таких задач появляется несколько целей, обусловленных наличием критериев, которые желательно оптимизировать. Однако, как правило, эти цели противоречивы, что вносит в задачу неопределенность, преодолеть которую формальными методами нельзя. Например, естественно стремление разработчика проекта автомобильной дороги сделать ее такой, чтобы она была «получше», а затраты «поменьше». Однако найти решение, удовлетворяющее обоим устремлениям, невозможно. Выход из создавшегося положения находится в поиске компромисса, т.е. решения - не полностью, а в какой-то степени удовлетворяющего и один, и другой критерий. Для облегчения принятия решения в условиях многокритериальных задач можно использовать такие процедуры, как «линейная свертка», «выделение основного критерия» и «ранжирование вариантов» и др. В данном случае для эффективного решения воспользуемся принципом Парето – важнейшим из принципов отбора рациональных решений. Этот принцип позволяет отбросить все те решения (альтернативы выбора), которые могут быть заменены другими, обеспечивающими лучшие значения целевых функций [6].

Рассмотрим задачу выбора направления автомобильной дороги. Пусть определены n допустимых вариантов уклонов трассирования i₁, i₂, . . ., i_n. Следовательно, для трассирования мы располагаем n значениями уклонов. Представим, что между начальными и конечными пунктами простирается водораздел с к седлами, определяющими возможные направления автомобильной дороги.

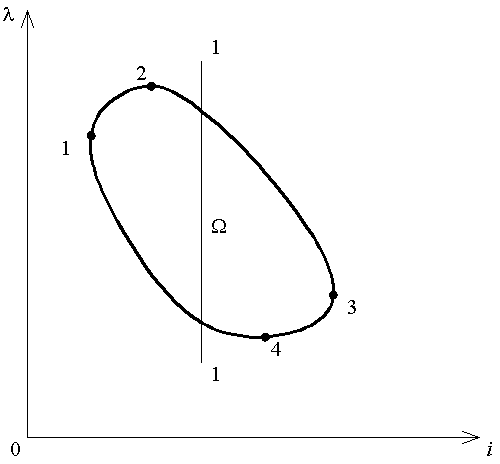
Рисунок 2 – Выделение конкурентных вариантов

Теоретически число r возможных вариантов трассы равно r = к_·n и может быть большим. Например, при к = 5 и n = 4 число вариантов трассы r = 20. Принимая во внимание, что проектирование каждого варианта для получения результата – приведенных строительно-эксплуатационных затрат – требует много труда и времени, попытаемся уменьшить их число. Запроектируем на карте n магистральных хода через все седла с уклонами i₁, i₂, . . ., i_n; всего к_·n магистральных ходов. Для каждого магистрального хода определим коэффициент удлинения λ. В результате для каждого варианта трассы получим два показателя: уклон i и коэффициент удлинения λ. Для наглядности представим каждый вариант в виде точки в системе координат iО λ (рисунок 2). На плоскости множеству допустимых вариантов соответствует область Ω. Цифрами 1, 2, 3 и 4 обозначим крайние точки области Ω.

Точке 1 соответствует минимум, а точке 3 – максимум уклона, точке 2 – максимум, а точке 4 – минимум коэффициента удлинения. Анализ показывает, что варианты с меньшими уклонами лежат на левой границе области Ω (дуга 2 – 1 – 4), а варианты с меньшими коэффициентами удлинения лежат на нижней границе области Ω (дуга 1 – 4 – 3). Общим для дуг 2 – 1 – 4 и 1 – 4 – 3 является их отрезок 1 – 4. Для вариантов, лежащих на дуге 1 – 4, справедлива следующая зависимость между i и λ: чем больше i, тем меньше λ. Для дуг 1 – 2 и 4 – 3 зависимость между i и λ имеет иной характер: чем больше i, тем больше λ. Понятно, что варианты с такой зависимостью между i и λ неприемлемы. На дуге 2 – 3 зависимость между i и λ такая же, как и на дуге 1 – 4, но варианты, принадлежащие дуге 2 – 3, имеют больший коэффициент удлинения, чем варианты, относящиеся к отрезку 1 – 4, например в сечении 1 – 1. Значит, только варианты, лежащие на дуге 1 – 4, должны разрабатываться и принимать участие в процедуре принятия решения.

Множество вариантов дуги 1 – 4 является множеством Парето [6]. Пары чисел i и λ, характеризующие множества Парето, образуют доминирующую последовательность. Для построения доминирующей последовательности можно использовать следующий практический прием. Пусть имеется неупорядоченная совокупность n пар чисел x и y: (x₁, y₁), (x₂, y₂), . . . , (x_n, y_n). Выстроим эти пары чисел в порядке возрастания x. Полученная последовательность ранжирована по x. В ранжированной по x последовательности между числами x_i существуют отношения

x₁ < x₂ < . . . < x_n,

числа же y находятся в произвольных отношениях. Далее проведем операцию просеивания пар (x,y). Для этого сравним в ранжированной по x последовательности пар (x, y) соседние величины y и пары, у которых

y_i ≤ y_{i – 1} ,

т.е. последующая величина y меньше или равна предыдущей, и исключим их из ранжированной последовательности. Оставшаяся от ранжированной последовательности совокупность пар образует доминирующую последовательность, в которой для чисел x и y справедливы отношения:

x₁ < x₂ < . . . < x_n;

y₁ < y₂ < . . . < y_n.

Доминирующая последовательность является информацией для принятия решения. Рассмотрим процедуру Парето на примере выбора вариантов направления автомобильной дороги.

Решается задача выбора направления автомобильной дороги для трассирования. Топографические условия проектирования таковы, что имеется три различных направления автомобильной дороги, определяемые фиксированными точками – седлами водораздела, располагающегося между опорными пунктами. В результате процедуры формирования множества допустимых вариантов [5] выявлены три варианта с разными уклонами. Для всех трех вариантов по всем трем направлениям уложены магистральные ходы и определены коэффициенты удлинения (таблица 2). Данные таблицы 2 иллюстрируются рисунком 3.

Расположим пары чисел λ и i в порядке возрастания λ (таблица 3). Такая упорядоченная последовательность пар λ и i является ранжированной по λ последовательностью.

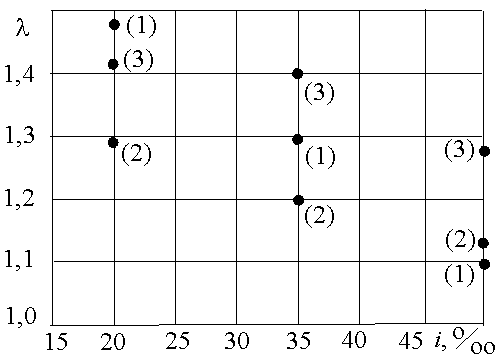
Рисунок 3 – Множество вариантов магистральных ходов

Таблица 2 – Коэффициенты удлинения магистральных ходов

Номер седла	1			2			3
Номер варианта	0	2	4	0	2	4	0	2	4
i, ‰	35	20	50	35	20	50	35	20	50
λ	1,30	1,48	1,09	1,20	1,29	1,13	1,40	1,42	1,28

Таблица 3 – Ранжированная по λ последовательность пар (λ, i)

Номер пары	1	2	3	4	5	6	7	8	9
Номер седла	1	2	2	3	2	1	3	3	1
λ	1,09	1,13	1,20	1,28	1,29	1,30	1,40	1,42	1,48
i, о/оо	50	50	35	50	20	35	35	20	20

Для сокращения числа вариантов применим к последовательности в таблице 3 операцию просеивания и в результате получим доминирующую последовательность (множество Парето) пар чисел (λ, i), определяющую варианты направлений и соответствующие им уклоны (таблица 4).

Таблица 4 – Конкурентные варианты направлений и уклонов

Номер ранжированной последовательности	1	3	5
Номер седла	1	2	2
λ	1,09	1,20	1,29
i, о/оо	50	35	20

Из таблицы 4 следует, что трассированию подлежат: через седло 1 вариант с i = 50 ^о/_оо, через седло 2 варианты с i = 35 ^о/_оо и i = 20 ^о/_оо. Таким образом, число вариантов для трассирования сократилось с 9 до 3.

Заключение

Ускоренное развитие техники и создание новых безотходных, энергосберегающих технологий приводит к значительному увеличению объемов и сложности проектно-конструкторских разработок. В таких условиях традиционные методы проектирования ограничивают возможность многовариантных подходов и не позволяют осуществить оптимизацию проектных решений, возникает противоречие между существующими потребностями и возможностями проектно-конструкторских организаций и коллективов.

Оптимизацию проектных решений при проектировании автомобильных дорог можно условно разделить на два уровня. Первый предусматривает рассмотрение всех вариантов, которые технически возможно осуществить в заданных местных условиях для проектируемого объекта с учетом всех его особенностей. Второй уровень оптимизации предусматривает перебор всех возможных сочетаний параметров вариантов, намеченных к проектированию. Для определения необходимой последовательности производства экспериментов, а также сокращения числа вычислительных процедур, предлагается применить метод Фибоначчи и принцип Парето.

Использование чисел Фибоначчи позволяет сократить общее число вариантов, подлежащих рассмотрению. В рассматриваемом примере при определении оптимальной глубины выемки общее число вариантов сократилось в три раза. Недостаток метода Фибоначчи заключается в том, что в нем априори необходимо задавать число испытаний n, так как на первом этапе поиска требуется вычислять n-oe и (n–1) -ое числа Фибоначчи для определения интервала неопределенности. Это можно произвести выбором соответствующего масштаба или точности расчета.

При наличии нескольких критериев для выявления оптимального решения предлагается использовать принцип Парето, что в рассматриваемом примере позволило сократить число вариантов также в три раза. Доминирующая последовательность, полученная в результате применения принципа Парето, является информацией для ЛПР. Для поиска компромиссного решения можно использовать «метод уступок» или «метод идеальной точки».

Предлагаемые методы оптимизации позволяют производить все необходимые расчеты непосредственно на компьютере, в вариантном исполнении, они могут являться одними из основных модулей в создании информационных моделей проектирования автомобильных дорог.

Литература

1 Бабков, В.Ф., Андреев, О.В. Проектирование автомобильных дорог.– Ч.1. 2-е изд. перераб. и доп. М.: Транспорт, 1987. – 368 с.

2 Изыскания и проектирование железных дорог / И.В. Турбин [и др]. – М. : Транспорт, 1989. – 400 с.

3 Соболь, Б.Ф., Месхи, Б.Ч., Каныгин, Г.И. Методы оптимизации. Практикум. М.: Феникс, 2009. – 384 с.

4 Аттетков, А.В., Галкин, С.В., Зарубин, В.С. Методы оптимизации. М.: МГТУ им. Н. Э. Баумана, 2003.

5 Воробьев, Н.Н. Числа Фибоначчи. М.: Наука,. 1969.

6 Подиновский, В.В., Ногин, В.Д. Парето-оптимальные решения многокритериальных задач. М.: Физматлит, 2007. – 256 с.