Контрольные вопросы
Способы реализации случайных событий в S-моделях.
Перечислите категории функций, входящих в инструментальное приложение StatisticsToolbox.
Сформулируйте алгоритм моделирования случайного события с использованием блока Fcn раздела Function&Tables.
Технология использования в S-модели генераторов случайных чисел приложения StatisticsToolbox.
Алгоритм моделирования случайного события по пороговому значению признака.
Схема моделирования случайного события по заданному диапазону признака.
ЛАБОРАТОРНАЯ РАБОТА №5
Управление модельным временем
5.1. ЦЕЛЬ РАБОТЫ
Рассмотрение способов управления модельным временем.
5.2. ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ
Задача корректного управления модельным временем, то есть «временем жизни» моделируемой системы, возлагается на разработчика независимо от того, какие инструменты создания модели он использует. Принципиальное отличие Simulink от универсальных средств программирования состоит в том, что логическая структура S-модели не зависит от способа управления модельным временем. Более того, исследователь может выбирать способ изменения модельного времени для каждого сеанса моделирования индивидуально. Тем не менее и при использовании Simulink модельное время остается «спинным мозгом», согласующим работу всех компонент S-модели. Поэтому при подготовке каждого модельного эксперимента должны быть получены ответы на три вопроса.
Какой способ изменения (приращения) времени целесообразно использовать (с постоянным или переменным шагом)?
С какой дискретностью следует изменять модельное время?
Какое событие будет служить условием окончания эксперимента?
После того, как вы ответите себе на каждый из этих вопросов, следует подумать о том, как воплотить намеченное в жизнь, используя средства Simulink.
5.2.1. Выбор шага моделирования
Напомним, что в практике имитационного моделирования применяются два основных способа изменения модельного времени ‑ с постоянным шагом и по особым состояниям. С точки зрения разработчиков Simulink ведущую роль при выборе одного из двух методов играет тип моделируемой системы: для непрерывных систем (с непрерывным временем смены состояний) по умолчанию используется переменный шаг приращения времени, а для дискретных систем следует устанавливать постоянный (фиксированный) шаг. Такой подход не всегда оправдывает себя, поскольку при моделировании непрерывных систем бывает удобнее определять очередное состояние системы как функцию времени, изменяющегося с заданной дискретностью. И наоборот, при моделировании дискретных систем величина очередного приращения времени зачастую определяется прогнозируемым моментом изменения состояния системы; причем смена состояний происходит, как правило, нерегулярно. Поэтому полезно знать, каким образом при разработке моделей дискретных систем можно заставить модельное время изменяться по особым состояниям.
С целью пояснения сказанного вернемся к примеру с накопителями. В разрабатываемой модели оценки загрузки накопителей фактор времени непосредственно не учитывался: была задана только длительность интервала моделирования, равная 10 единицам модельного времени. По умолчанию предполагалось, что данные поступают на каждый из накопителей через интервалы времени, определяемые дискретностью изменения модельного времени (∆t=0,2). Вместе с тем, распределение входных воздействии во времени ‑ важнейшая характеристика рабочей нагрузки системы. Какие же средства Simulink позволяют управлять величиной шага моделирования при изменении модельного времени по особым состояниям?
В первую очередь это «связка» из двух уже знакомых вам блоков MATLAB Fen и Discrete-Time Integrator. Блок MATLAB Fen обеспечивает формирование отрезков времени, длина которых распределена по заданному закону, а блок Discrete Time Integrator выполняет суммирование этих отрезков, то есть «продвижение» модельного времени. Таким образом, с помощью этих двух блоков можно реализовать механизм изменения модельного времени по особым состояниям для таких S-моделей, в которых условием наступления очередного события является истечение некоторого промежутка времени.
В рассматриваемом примере таким событием является поступление на вход системы очередного сообщения, интервал времени между соседними сообщениями является случайной величиной, распределенной по заданному закону. Пока для простоты будем считать, что запись информации на накопители происходит мгновенно, и величина приращения модельного времени определяется только промежутком времени до появления очередной порции информации.
С учетом внесенных дополнений модель работы накопителя будет выглядеть так, как показано на рис.5.1 (для второго накопителя блок-диаграмма строится аналогичным образом).
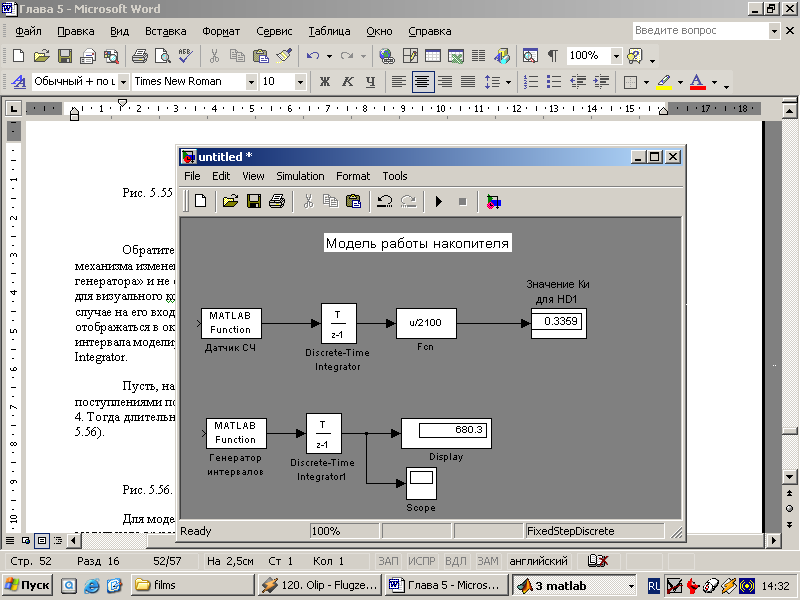
Рис. 5.1. Изменение модельного времени по особым состояниям
Обратите внимание на следующее весьма важное обстоятельство: при такой реализации механизма изменения модельного времени собственный таймер Simulink играет роль «тактового генератора» и не определяет непосредственно длительность интервала моделирования. При таком подходе для визуального контроля за изменением модельного времени по-прежнему пригоден блок Scope. В этом случае на его вход следует подавать сигнал с блока Discrete-Time Integrator, значения которого будут отображаться в окне Scope как функция от номера шага моделирования. Соответственно, длительность интервала моделирования будет равна последнему значению сигнала на выходе блока Discrete-Time Integrator.
Пусть, например, параметр Stop time по-прежнему будет равен 10, а интервалы времени между поступлениями порций информации распределены по нормальному закону с параметрами m=10; v=4. Тогда длительность интервала моделирования работы накопителей составит в среднем 90 с (рис. 5.2).
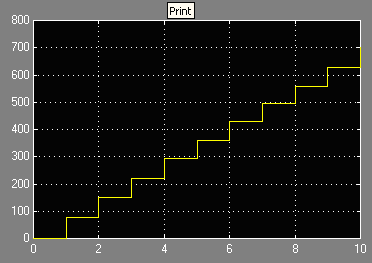
Рис. 5.2. Отображение модельного времени в блоке Scope
Для моделирования непрерывных систем более удобным является изменение модельного времени с постоянным шагом. Чтобы реализовать этот механизм в создаваемой модели, вполне достаточно стандартных средств управления экспериментом, имеющихся в диалоговом окне Simulation Parameters. Хотя эти средства уже упоминались ранее, полезно рассмотреть их применение на конкретном примере, в качестве которого используем ситуацию, приведенную в первой части книги. Речь шла о том, что некий самолет движется прямолинейно и с постоянной скоростью, а следящий за ним диспетчер должен ввести информацию о самолете до того, как он пересечет заданный рубеж.
Блок-диаграмма модели, описывающей данную ситуацию, изображена на рис. 5.3.
Назначение блоков, входящих в модель, указано в самой диаграмме. Остается только добавить, что блок Int1 вычисляет расстояние, пройденное самолетом, а блок Int2 ‑ количество введенных диспетчером символов.
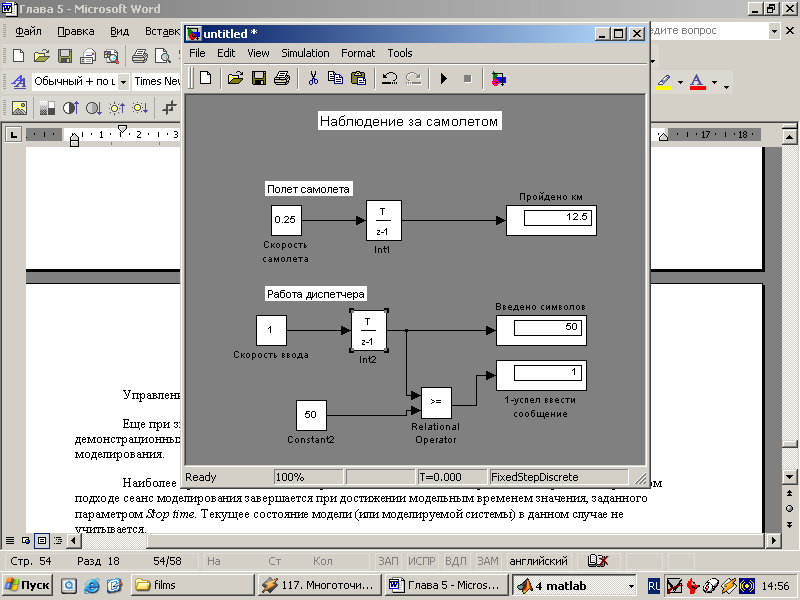
Рис. 5.3. Пример моделирования с постоянным шагом
Для определенности будем считать, что фигурирующие в модели величины имеют следующие значения:
скорость самолета – 900 км/ч;
расстояние до рубежа ‑ 12,5 км;
скорость ввода информации ‑ 1 символ в секунду;
длина текста – 50 символов.
Прежде чем установить параметры моделирования, мы должны выполнить следующие действия.
1. Привести скорость полета самолета и работу оператора к единому масштабу времени.
2. Выбрать величину шага приращения модельного времени.
3. Определить приемлемую длительность интервала моделирования.
Первый пункт выполнить проще всего: выражаем скорость самолета в км/с и получаем 0,25 км/с. Выполнение второго пункта требует сопоставления скоростей двух процессов; сравнив скорости, выберем ∆t=1 с. Для выполнения третьего пункта также вполне достаточно выполнить одно-два арифметических действия.
Конечно, простота рассматриваемого примера вызывает сильное желание посчитать все вручную, но нас в данном случае интересует не столько результат, сколько процесс создания модели.
Итак, устанавливаем следующие параметры моделирования:
• Stop time: 50;
• Type: Fixed step;
• Fixed step size: 2.
Последний параметр требует дополнительного пояснения: для всех блоков, имеющих параметр Sample time, он также должен быть равен 2. Соответствие результата моделирования ручным расчетам говорит о том, что созданная модель работает корректно. Выполнив сеанс моделирования, получаем ответ на поставленный ранее вопрос: диспетчер успеет (хотя и с трудом) ввести требуемую информацию.
Казалось бы, при неизменных исходных данных такой результат должен получаться всегда. Но не следует забывать о той роли, которую играет выбор шага моделирования (то есть величины ∆t). Установите значение Fixed step size: 3 и повторите моделирование. Теперь диспетчер «не успевает» ввести сообщение, сколько бы раз вы не повторяли эксперимент.