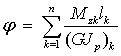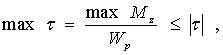Рациональные формы поперечных сечений при изгибе.
Наиболее рациональным
следует признать сечение, обладающее
минимальной площадью при заданной
нагрузке (изгибающем моменте) на балку.
В этом случае расход материала на
изготовление балки, будет минимальным.
Для получения балки минимальной
материалоемкости нужно стремиться к
тому, чтобы по возможности наибольший
объем материала работал при напряжениях,
равных допускаемым или близким к ним.
Прежде всего рациональное сечение балки
при изгибе должно удовлетворять условию
равнопрочности растянутой и сжатой зон
балки. Иными словами
необходимо, чтобы наибольшие напряжения
растяжения (max
)
н наибольшие напряжения сжатия (max
)
одновременно достигали допускаемых
напряжений
и
.
Поэтому для балки
из пластичного материала (одинаково
работающего на растяжение и сжатие:
),
условие равнопрочности выполняется
для сечений, симметричных относительно
нейтральной оси. К таким сечениям
относится, например, прямоугольное
сечение (рис. 26, а),
при котором обеспечено условие равенства
.
Однако в этом случае материал, равномерно
распределенный по высоте сечения, плохо
используется в зоне нейтральной оси.
Чтобы получить более рациональное
сечение, необходимо возможно большую
часть материала переместить в зоны,
максимально удаленные от нейтральной
оси. Таким образом, приходим к
рациональному для пластичного материала
сечению в форме симметричного
двутавра (рис. 26):
2 горизонтальных
массивных листа, соединенные
стенкой (вертикальным листом), толщина
которой
назначается
из условий прочности стенки по касательным
напряжениям, а также из соображений ее
устойчивости. К двутаврому сечению
близко по критерию рациональности так
называемое коробчатое сечение (рис. 26,
в).
Рис.
26.
Распределение нормальных напряжений
в симметричных сечениях
Рассуждая аналогично, приходим к выводу, что для балок из хрупкого материала наиболее рациональным будет сечение в форме несимметричного двутавра, удовлетворяющего условию равнопрочности на растяжение и сжатие (рис. 27):
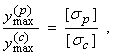
которое вытекает из требования
Рис.27.
Распределение напряжений несимметричного
профиля сечения балки.
Идея рациональности поперечного сечения стержней при изгибе реализована в стандартных тонкостенных профилях, получаемых методами горячего прессования или прокатки из рядовых и легированных конструкционных высококачественных сталей, а также алюминия и алюминиевых сплавов, получивших широкое распространение в строительстве, машиностроении, авиационном машиностроении. Широко распространены показанные на рис. 27: а—двутавр, б— швеллер, в — неравнобокий уголок, г—равнобокий уголок. Реже встречаются тавр, таврошвеллер, зетовый профиль и др.
Рис.11.
Используемые профили сечений: а) двутавр,
б ) швеллер, в) неравнобокий уголок, г)
равнобокий уголок
6. Кручение Закон Гука при сдвиге
Кручением называют деформацию, возникающую при действии на стержень пары сил, расположенной в плоскости, перпендикулярной к его оси (рис. 23).
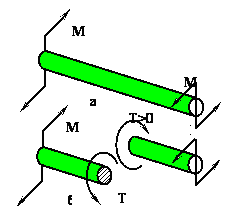
Рис.23.
Стержни круглого или кольцевого сечения, работающие на кручение, называют валами. Касательные напряжения τ и угловая деформация γ связаны законом Гука при сдвиге:
τ = Gγ,
где G - модуль упругости второго рода или модуль сдвига. Модуль сдвига является характеристикой материала. Для изотропного материала модуль сдвига связан с модулем Юнга E и коэффициентом Пуассона μ определенной зависимостью:
G= E/2(1+ μ).
Напряжения и деформации при кручении стержней кругового поперечного сечения
Кручением называется такой вид деформации, при котором в поперечном сечении стержня возникает лишь один силовой фактор — крутящий момент Мz. Крутящий момент по определению равен сумме моментов внутренних сил относительно продольной оси стержня Oz. Нормальные силы, параллельные оси Oz, вклада в крутящий момент не вносят. С силами, лежащими в плоскости поперечного сечения стержня (интенсивности этих сил — касательные напряжения и ) Мz связывает вытекающее из его определения уравнение равновесия статики (рис. 24)
Условимся считать Mz положительным, если со стороны отброшенной части стержня видим его направленным против часовой стрелки. Это правило проиллюстрировано на рис. 25 и в указанном соотношении, где крутящий момент Мz принят положительным. Численно крутящий момент равен сумме моментов внешних сил, приложенных к отсеченной части стержня, относительно оси Ог.
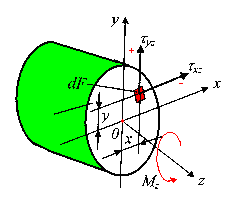Рис.24.
Связь крутящего момента с касательными
напряжениями
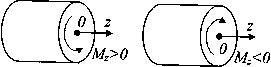Рис.25.
Иллюстрация положительного и отрицательного
крутящего момента
Рассмотрим кручение призматических стержней кругового поперечного сечения. Исследование деформаций упругого стержня с нанесенной на его поверхности ортогональной сеткой рисок (рис. 26) позволяет сформулировать следующие постудаты теории кручения этого стержня:
поперечные сечения остаются плоскими (выполняется гипотеза Бернулли);
расстояния между поперечными сечениями не изменяются, следовательно
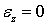;контуры поперечных сечений и их радиусы не деформируются. Это означает, что поперечные сечения ведут себя как жесткие круговые пластинки, поворачивающиеся при деформировании относительно оси стержня Оz. Отсюда следует, что любые деформации в плоскости пластинки равны нулю, в том числе и
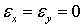;материал стержня подчиняется закону Гука. Учитывая, что
,
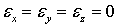из обобщенного закона Гука в форме
получаем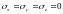
.
Это означает, что в поперечных сечениях,
стержня возникают лишь касательные
напряжения
,
а вследствие закона парности касательных
напряжений, равные им напряжения
действуют и в сопряженных продольных
сечениях. Следовательно напряженное
состояние стержня — чистый
сдвиг.
Рис.26.
Иллюстрация кручения: а)
исходное и б)
деформированное состояния
Выведем формулу
для касательных напряжений при кручении
призматического стержня кругового
поперечного сечения. Как видно, поворот
правого торцевого сечения относительно
неподвижного левого на угол
(назовем
его углом закручивания стержня) вызывает
поворот продольных волокон на угол
(угол
сдвига), поскольку на величину
искажаются
углы ортогональной сетки продольных и
поперечных рисок модели.
Двумя смежными
сечениями вырежем элемент стержня
длиной dz
и, поскольку нас интересуют деформации
элемента, левое сечение его будем считать
неподвижным (рис. 27). При повороте правого
сечения на угол
в
соответствии с гипотезой о недеформируемости
радиусов, правый конец волокна АВ
(отстоящий от оси элемента на величину
полярного радиуса
)
будет перемещаться по дуге BB1,
вызывая поворот волокна на угол сдвига
Обратим внимание на то, что в соответствии с рис. 5 и рис. 6, а сдвиг и связанное с ним касательное напряжение перпендикулярны радиусу . Определим , воспользовавшись законом Гука для чистого сдвига
|
(1) |
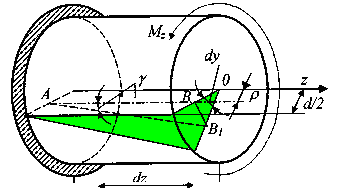Рис.27.
Расчетная модель определения касательных
напряжений
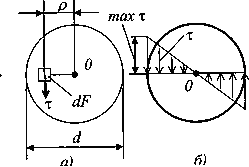а)
ортогональность
и
Рис.28.
Распределение касательных напряжений
при кручении:
Здесь
—
погонный угол закручивания стержня,
который остается пока неизвестным. Для
его нахождения обратимся к условию
статики, записав его в более удобной
для данного случая форме (рис. 28, a)
|
(2) |
Подставляя (1) в (2) и учитывая, что
где Jp—;
полярный момент инерции поперечного
сечения (для круга с диаметром d
),
получаем
|
(3) |
Подставляя
выражение (3) в (1), получаем формулу для
касательных напряжений при кручении
призматического стержня кругового
поперечного сечения
|
(4) |
Как видно из (4), сдвиги и касательные напряжения пропорциональны расстояний от оси стержня. Обратим внимание на структурные аналогии формул для нормальных напряжений чистого изгиба и касательных напряжений кручения.
Мерой деформации стержня при кручении является погонный угол закручивания стержня, определяемый по (3). Поскольку величина GJp стоит в знаменателе формулы и при заданной нагрузке (Mz через нее выражается) тем меньше, чем больше GJp, последнюю называют жесткостью поперечного сечения при кручении.
Пользуясь (3) для определения угла закручивания элемента длиной dz
найдем полный угол закручивания стержня длиной l
|
(5) |
В
случае, если по длине стержня Мz
и GJp
постоянны, получаем
когда эти величины кусочно-постоянны, то:
|
(6) |
Отметим, что полученные формулы по структуре аналогичны формулам для деформаций при растяжении стержня.
Наибольшие касательные
напряжения возникают у внешней поверхности
стержня, т. е. при
где Wр — момент сопротивления при кручении или полярный момент сопротивления
.
Полярный момент сопротивления, стоящий в знаменателе для максимальных касательных напряжений, очевидно, является геометрической характеристикой сечения, а условие прочности стержня при кручении принимает вид
|
(7) |
где
—
допускаемое напряжение на кручение.
Как показали эксперименты и точное решение этой задачи в теории упругости, все гипотезы, сформулированные ранее для стержня со сплошным круговым сечением, остаются справедливыми и для стержня кольцевого поперечного сечения (рис. 7). Поэтому все выведенные ранее формулы пригодны для расчета стержня кольцевого сечения с той лишь разницей, что полярный момент инерции определяется как разность моментов инерции кругов с диаметрами D и d
где
,
а момент сопротивления определяется
по формуле
Учитывая линейный характер изменения касательных напряжений по радиусу (рис. 7) и связанное с этим лучшее использование материала, кольцевое сечение следует признать наиболее рациональным при кручении стержня. Коэффициент использования материала тем выше, чем меньше относительная толщина трубы.
Как отмечено
ранее, напряженное состояние при кручении
стержня — чистый сдвиг, являющийся
частным случаем плоского напряженного
состояния. На площадках, совпадающих с
плоскостью поперечного сечения и на
парных им площадках продольных сечений
возникают экстремальные касательные
напряжения max-min
,
а главные напряжения
действуют
на площадках, наклоненных.коси стержня
под углами
;
главное напряжение
.
Особенности
напряженного состояния при кручении
нашли отражение в характере разрушения
стержней. Так, разрушение стержня из
дерева, плохо работающего на скалывание
вдоль волокон, происходит от продольных
трещин (рис. 29, a). Разрушение стержня из
хрупкого металла (например, чугуна)
происходит по винтовой линии, наклоненной
к образующим под углом 45o,
т. е. по траектории главного напряжения
(рис.
29,б).
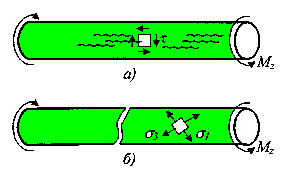Рис.29.
Распределение исходных касательных и
главных напряжений: а) разрушение дерева,
б) разрушение чугуна
ПРИЛОЖЕНИЕ 1.
Допущения, применяемые в сопротивлении материалов
Для построения теории сопротивления материалов принимают некоторые допущения относительно структуры и свойств материалов, а также о характере деформаций. Приведем основные из них.
1. В сопротивлении материалов принято рассматривать все материалы как однородную сплошную среду, независимо от их микроструктуры. Под однородностью материала понимают независимость его свойств от величины выделенного из тела объема. И хотя в действительности реальный материал, как правило, неоднороден (уже в силу его молекулярного строения), тем не менее, указанная особенность не является существенной, поскольку в сопротивлении материалов рассматриваются конструкции, размеры которых существенно превышают не только межатомные расстояния, но и размеры кристаллических зерен.
С понятием однородности тесно связано понятие сплошности среды, под которым подразумевают тот факт, что материал конструкции полностью заполняет весь отведенный ему объем, а значит в теле конструкции нет пустот. Это допущение позволяет использовать в сопротивлении материалов методы математического анализа (дифференциальное и интегральное исчисления).
2. Обычно сплошная среда принимается изотропной, т.е. предполагается, что свойства тела, выделенного из нее, не зависят от его ориентации в пределах этой среды. Материалы, имеющие различные свойства в разных направлениях, называют анизотропными (например, дерево). Отдельно взятый кристалл материала анизотропен, но т.к. в объеме реального тела содержится бесконечно большое количество хаотично расположенных кристаллов, принимается, что материал изотропен.
Металлы и сплавы, как правило, изотропны. В настоящее время широкое распространение получили анизотропные композиционные материалы, состоящие из двух компонентов – наполнителя и связующего. Наполнитель состоит из уложенных в определенном порядке высокопрочных нитей – матрицы, что и определяет значительную анизотропию композита. Композиционные материалы имеют высокую прочность при значительно меньшем, чем металлы весе.
3. Принимается, что до определенной величины деформации материалов подчиняются закону Гука и весьма малы относительно размеров тела, поэтому все расчеты выполняются по исходной, т.е. недеформированной, схеме, к которой применим принцип независимости действия сил.
4. После снятия нагрузки геометрические размеры тела полностью или частично восстанавливаются. Свойство тела восстанавливать свои первоначальные размеры после разгрузки называется упругостью. При решении большинства задач в сопротивлении материалов принимается, что материал конструкций абсолютно упругий. Это допущение справедливо, пока нагрузки не превышают определенного значения. При больших нагрузках в элементах конструкций появляются пластические деформации.
5. Перемещения, возникающие под действием внешних сил в упругом теле, малы по сравнению с его размерами. Это допущение называется принципом начальных размеров. Допущение позволяет при составлении уравнений равновесия пренебречь изменениями формы и размеров конструкции.
6. Предполагается, что в сечениях, достаточно удаленных от мест приложения нагрузки, характер распределения напряжений не зависит от конкретного способа нагружения. Основанием для такого утверждения служит принцип Сен-Венана, справедливый для любого типа напряженного состояния и формулируемый следующим образом: особенности приложения внешних нагрузок проявляются, как правило, на расстояниях, не превышающих характерных размеров поперечного сечения стержня.
7. Принимается гипотеза плоских сечений (гипотеза Бернулли), введенной швейцарским ученым Д. Бернулли, гласящей, что плоские поперечные сечения стержня до деформации остаются плоскими и после деформации.
8. Считается, что ненагруженное тело свободно от каких бы то ни было внутренних сил любой природы.
ПРИЛОЖЕНИЕ 2.
Формирование тензометрических мостовых схем |
Тензорезисторы предназначены для измерения напряжений возникающих на поверхности различных деталей. С помощью тензорезисторов можно измерять степень сжатия и растяжения, скручивания, изгиба. При известном модуле Юнга и профиле изделия можно расчитать прикладываемые к изделию силы.
В таблице приведены различные схемы подключения тензорезисторов. Имеется возможность исключения различных влияющих факторов на измерения, например, влияние температуры.
Наименование |
Пример |
Схема |
Выход |
Один активный тензорезистор, двухпроводная схема подключения. Применима при малых изменениях температуры. Без термокомпенсации. x1 выход. Изгиб также влияет на измерения. |
|||
1 активный тензорезистор 2-х проводная схема включения Число тензорезисторов: 1 |
|
|
e0 = (E/4)·Ks·ε0 Ks – K-фактор ε0 – деформация E – питание моста e0 – выходное напряжение Rg – сопротивление тензорезистора R – постоянное сопротивление |
Один активный тензорезистор, трехпроводная схема подключения. Без термокомпенсации. Температурная погрешность кабеля исключена. x1 выход. Изгиб влияет на измерения. |
|||
1 активный тензорезистор 3-х проводная схема включения Число тензорезисторов: 1 |
|
|
e0 = (E/4)·Ks·ε0 |
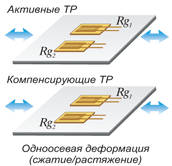
Два активных тензорезистора, двухпроводная схема включения. Без термокомпенсации. Деформация изгиба исключена. х1 выход. |
|||
Двойная 1 активный тензорезистор 2-х проводная схема включения (для исключения деформации изгиба) Число тензорезисторов: 2 |
|
|
e0 = (E/4)·Ks·ε0 Rg1..деформация – ε1 Rg2..деформация – ε2 ε0 = (ε1+ε2)/2 R – постоянное сопротивление R = Rg1+Rg2 |
Два активных тензорезистора, трехпроводная схема включения. Без термокомпенсации. Деформация изгиба исключена. Температурная погрешность кабеля исключена. х1 выход. |
|||
Двойная. 1 активный тензорезистор 3-х проводная схема включения (для исключения деформации изгиба) Число тензорезисторов: 2 |
|
|
e0 = (E/4)·Ks·ε0 Rg1..деформация – ε1 Rg2..деформация – ε2 ε0 = (ε1+ε2)/2 R – постоянное сопротивление R = Rg1+Rg2 |
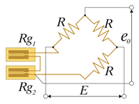
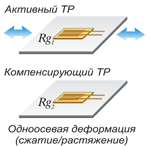
Два тензорезистора: активный и компенсационный. Термокомпенсирована. Температурная погрешность кабеля исключена. х1 выход |
|||
2 активных тензорезистора (активный + компенсационный) Число тензорезисторов: 2 |
|
|
e0 = (E/4)·Ks·ε0 Ks – K-фактор ε0 – деформация E – питание моста e0 – выходное напряжение Rg1..деформация – ε1 R – постоянное сопротивление Rg2..деформация – 0 |
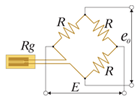
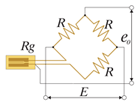
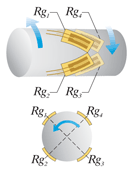
Два активных тензорезистора (ортогональное расположение). Термокомпенсирована. Температурная погрешность кабеля исключена. х(1+ν) выход |
|||
Ортогональная 2 активных тензорезистора Число тензорезисторов: 2 |
|
|
e0 = ((1+ν)E/4)·Ks·ε0 ν – коэффициент Пуассона Rg1 Rg2 – сопротивление транзисторов Rg1..деформация – ε0 Rg2..деформация – νε0 R – постоянное сопротивление |
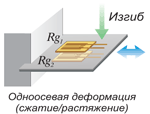
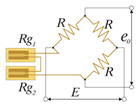
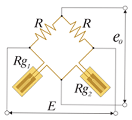
Два активных тензорезистора. Термокомпенсирована. Температурная погрешность кабеля исключена. Деформация сжатия/растяжение исключена. х2 выход |
|||
2 активных тензорезистора (для деформации изгиба) Число тензорезисторов: 2 |
|
|
e0 = (E/2)·Ks·ε0 Rg1..деформация – ε0 Rg2..деформация – -ε0 R – постоянное сопротивление |
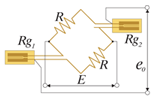
Два активных тензорезистора. Оппозитная схема. Без термокомпенсации. Деформация изгаба исключена подключением в противоположных направлениях. х2 выход. |
|||
Оппозитная. 2 активных тензорезистора 2-х проводная схема включения Число тензорезисторов: 2 |
|
|
e0 = (E/2)·Ks·ε0 Rg1..деформация – ε0 Rg2..деформация – ε0 R – постоянное сопротивление |
Два активных тензорезистора. Оппозитная схема. Без термокомпенсации. Температурная погрешность кабеля исключена. Деформация изгиба исключена. х2 выход. |
|||
Оппозитная. 2 активных тензорезистора 3-х проводная схема включения Число тензорезисторов: 2 |
|
|
e0 = (E/2)·Ks·ε0 Rg1..деформация – ε0 Rg2..деформация – ε0 R – постоянное сопротивление |
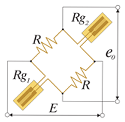
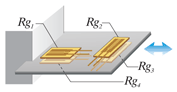
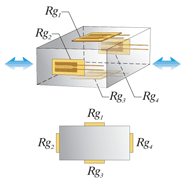
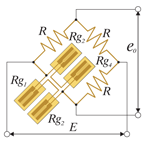
Четыре активных тензорезистора. Применима для измерений деформации изгиба. Термокомпенсирована. Температурная погрешность кабеля исключена. Деформация сжатия/растяжения исключена. х4 выход. |
|||
4 активных тензорезистора (для измерений деформации изгиба) Число тензорезисторов: 4 |
|
|
e0 = E·Ks·ε0 Rg1, Rg3 – деформация изгиба – ε0 Rg2, Rg4 – деформация изгиба – -ε0 |
Четыре активных тензорезистора. Термокомпенсирована. Температурная погрешность кабеля исключена. х2(1+v) выход. |
|||
Ортогональная 4 активных тензорезистора Число тензорезисторов: 4 |
|
|
e0 = ((1+ν)E/2)·Ks·ε0 ν - коэффициент Пуассона Rg1, Rg3 – деформация изгиба – ε0 Rg2, Rg4 – деформация изгиба – -ε0 |
Четыре активных тензорезистора. Термокомпенсация. Температурная погрешность кабеля исключена. Деформация изгиба исключена. х2 выход. |
|||
Активные + компенсационные Схема 4/4 Число тензорезисторов: 4 |
|
|
e0 = (E/2)·Ks·ε0 Rg1, Rg3 – деформация изгиба – ε0 Rg2, Rg4 – деформация изгиба – 0 |
Два активных тензорезистора. Применима для измерения деформации изгиба. Термокомпенсация. Температурная погрешность кабеля исключена. х2 выход. |
|||
2 активных тензорезистора (для измерений изгибающих деформаций) Число тензорезисторов: 2 |
|
|
e0 = (E/2)·Ks·ε0 Rg1..деформация – ε0 Rg2..деформация – -ε0 R – постоянное сопротивление |
Четыре активных тензорезистора. Применима для измерения деформации изгиба. Термокомпенсация. Температурная погрешность кабеля исключена. х4 выход. |
|||
4 активных тензорезистора (для измерений изгибающих деформаций) Схема 4/4 Число тензорезисторов: 4 |
|
|
e0 = E·Ks·ε0 Rg1, Rg3 – деформация изгиба – ε0 Rg2, Rg4 – деформация изгиба – -ε0 |
Четыре активных тензорезистора. Применима для измерения общей деформации. Без термокомпенсации. х1 выход. |
|||
4 активных тензорезистора (для измерения суммарной деформации) Число тензорезисторов: 4 |
|
|
e0 = (E/2)·Ks·ε0 ε0 = (ε1+ε2+ε3+ε4)/2 R – постоянное сопротивление R=Rg1=Rg2=Rg3=Rg4 |
