Построение эпюр напряжений
Нормальная сила N в произвольном сечении стержня определяется по методу сечений. Рассмотрим нагружение стержня сосредоточенными силами (рис.14.а). и равномерно распределённой нагрузкой qi = const (рис.14.б).
Рис.14.
В произвольном сечении бруса на участке АB нормальная сила N определяется из условия равновесия отсеченной части (рис. 14.б):
N = P1 – ql1 + qz .
При этом внешняя сила условно считается положительной, если растягивает рассматриваемый участок, и отрицательной, если сжимает.
Рассмотрим пример статически определимого стержня (рис. 15). Используя метод сечений, необходимо отбрасывать часть стержня с заделкой. Последовательно применяя метод сечений на каждом участке (i =1, 2, 3, 4), определяются нормальные силы на участках. По полученным значениям строится эпюра N. Скачки на эпюре N по величине равны силам, приложенным в соответствующих сечениях. Участок АВ не деформируется, участки ВС и DM растягиваются, а участок СD сжимается.
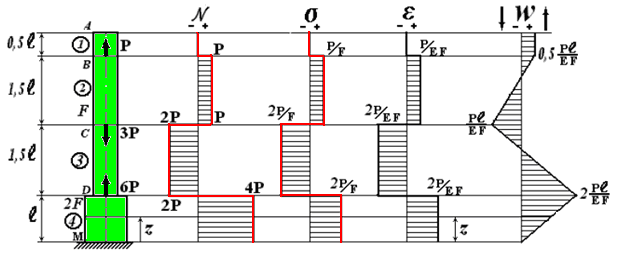
Рис.15.
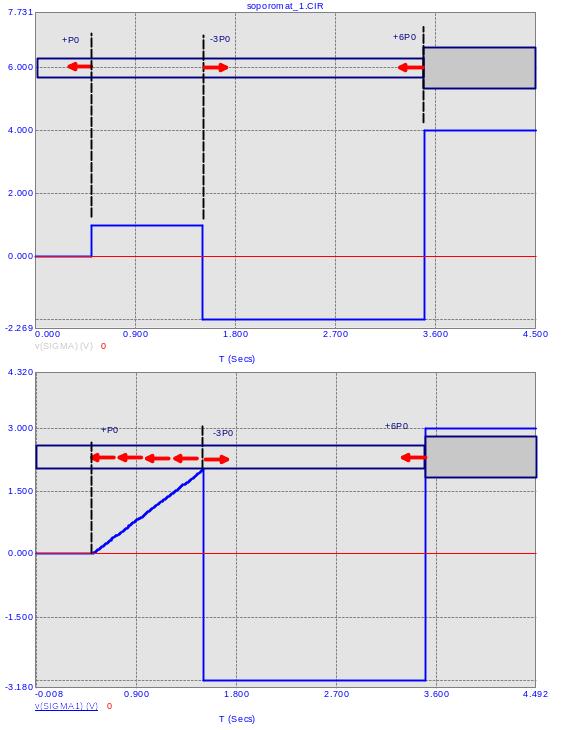
ПРИМЕР нетрадиционного использования возможностей МС-9 для решения предыдущего примера + вариант с распределённой силой
З-н
Ома:
сопротивление проводника:
З-
Гука:
Для моделирования длины полагаем:
l=t
5. Изгиб.
Вычисление моментов инерции и моментов сопротивления для простейших сечений.
Известно, что
интеграл вида
является
моментом инерции сечения относительно
нейтральной оси (ось, проходящая через
центр тяжести сечения: сечение, подвешенное
за эту точку, при повороте остается
неподвижным).
Здесь
—
расстояние элементарной площадки
dF
от нейтральной оси; суммирование
охватывает всю площадь сечения.
1. Покажем в качестве примера вычисление этого интеграла для прямоугольника (Рис.16) высотой h и шириной b. Проведем через его центр тяжести О оси симметрии Oz и Оу. Если внешние силы, действующие на балку, лежат в плоскости Oz, то нейтральной осью будет ось Оу. Найдем относительно этой оси сначала момент инерции, а потом и момент сопротивления площади прямоугольника.
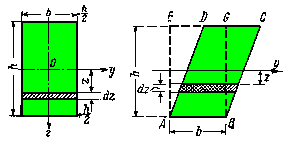Рис.16.
Расчетная модель для определения осевого
момента инерции прямоугольника.
Площадки dF, на которые следует разбить всю площадь сечения, выберем в виде узких прямоугольников шириной b и высотой dz (Рис.16.а). Тогда:
и интеграл J принимает вид:
Чтобы взять интеграл по
всей площади прямоугольника, следует
z
менять от
до
.
Тогда
.
Момент сопротивления
относительно нейтральной оси Оу
мы получим, разделив Jy
на
Если необходимо вычислить
момент инерции и момент сопротивления
прямоугольника относительно оси Oz,
то в полученных формулах следовало бы
b и
h
поменять местами:
и
Заметим, что сумма
произведений
не
изменится, если мы сдвинем все полоски
Df =
bdz
параллельно самим себе так, что они
расположатся в пределах параллелограмма
ABCD.
Иначе, момент инерции параллелограмма относительно оси у равен моменту инерции равновеликого ему прямоугольника
2. При вычислении
момента инерции круга
радиуса
(Рис.17)
также разбиваем площадь на узкие полоски
размером
вдоль
оси Oz;
ширина этих полосок b
= b(z)
тоже будет переменной по высоте сечения.
Элементарная площадка
Момент инерции равен:
Рис.17.
Расчетная модель для определения осевого
момента инерции кругового сечения.
Так как верхняя и нижняя половины сечения одинаковы, то вычисление момента инерции достаточно провести для одной нижней и результат удвоить. Пределами для изменения z будут 0 и :
Введем новую переменную
интегрирования — угол
(Рис.2);
тогда
Пределы: при
;
при
,
следовательно,
и
