1.7. Оценка запаса устойчивости и быстродействия по переходной характеристике (рисунок 12)

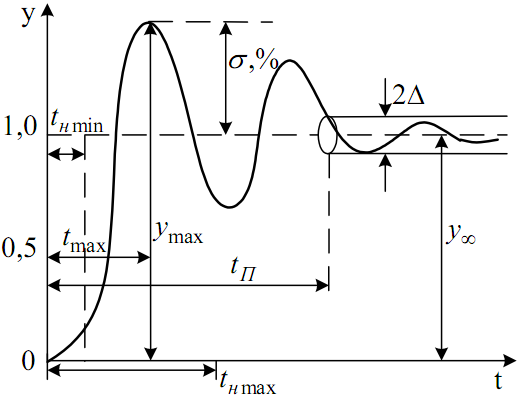
Рисунок 12. Переходная функция САР

Запас устойчивости САР оценивают по величине перерегулирования .

В таблице 7 приведены показатели качества, характерные для различных САР (часто применяемых, редко применяемых и т.д.).

Таблица 7. Варианты

Варианты
Применяемость	редко	часто	Избегают
Запас по фазе
Число колебаний

Быстродействие САР оценивают по времени окончания переходного процесса , при заданной допустимой ошибке .

от .

Время нарастания ограничено:

– допустимым ускорением координат и предельными колебательными режимами;

– требуемым быстродействием.

Следующий показатель качества характеризует число колебаний регулируемой величины в течении времени переходного процесса . В таблице 7 показано, что наиболее часто применяются САР с числом колебаний 1,2.

На рисунке 13 показаны дополнительные показатели качества регулирования:

- собственная частота колебаний системы , где – период собственных колебаний системы;

- логарифмический декремент затухания колебательного процесса , где и – две амплитуды для расположенных рядом экстремумов кривой переходного процесса;

- максимальная скорость отработки регулируемой величины .

Рисунок 13. Переходной процесс САР

2. Задание к лабораторной работе

2.1. С помощью программы MatchCAD провести моделирование переходного процесса АСУ в соответствии со схемой рисунок 14 и вариантом. Входное воздействие – единичное ступенчатое.

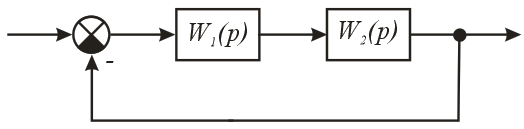
Рисунок 14. Структурная схема исследуемой САР

2.2. Записать передаточную функцию разомкнутой системы. Записать характеристическое уравнение системы. Определить устойчивость по критерию Рауса-Гурвица.

2.3. Построить АФЧХ разомкнутой системы, определить устойчивость АСУ по критерию Найквиста. Определить запасы устойчивости по модулю и фазе.

2.4. Построить ЛЧХ разомкнутой системы, определить устойчивость и запасы устойчивости по модулю и фазе.

2.5. По переходной характеристике АСУ определить основные и дополнительные показатели качества регулирования.

3. Варианты заданий

Варианты заданий представлены в таблице 6.

Таблица 6. Варианты заданий для выполнения лабораторной работы №4.

Вариант					, с	, с	, с
1			10	3	0,7	0,4	1,2
2			11	4	0,8	0,9	-
3			12	5	0,9	-	-
4			13	6	1	0,6	1,8
5			14	7	1,1	1,2	-
6			15	4	1,2	-	-
7			16	5	1,3	0,7	1,9
8			17	6	1,4	1,5	-
9			18	7	1,5	-	-
10			19	8	1,6	0,9	2,2
11			20	9	1,7	1,8	-
12			21	10	1,8	-	-
13			22	12	1,9	1	2,8
14			23	13	2	2,1	-
15			24	15	2,1	-	-
16			10	5	1	0,5	1,6
17			11	6	1,1	1,2	-
18			12	7	1,2	-	-
19			13	8	1,3	0,6	2
20			14	9	1,4	1,5	-
21			15	8	1,5	-	-
22			16	7	1,6	0,8	2,4
23			17	5	1,7	1,8	-
24			18	6	1,8	-	-
25			19	7	1,9	1	2,9
26			20	11	2	2,1	-
27			21	12	2,1	-	-
28			22	13	1,6	0,7	2,7
29			23	14	1,7	1,8	-
30			24	17	1,8		-