Лабораторная работа №4

Исследование устойчивости автоматических систем управления. Оценка качества регулирования

Цель работы: Применение критериев устойчивости для исследования систем автоматического регулирования, определение показателей качества регулирования систем.

1. Теоретическая часть

Понятие устойчивости системы регулирования связано с ее способностью возвращаться в состояние равновесия после исчезновения внешних сил, которые вывели ее из этого состояния.

1.1. Определение устойчивости по м.Я.Ляпунову

Невозмущенное движение (при ) называется устойчивым по отношению к переменным , если при всяком заданном положительном числе , как бы мало оно не было, можно выбрать другое положительное число , так, что для всех возмущений ,, удовлетворяющих условию , возмущенное движение будет для времени удовлетворять неравенству , где – коэффициенты, уравновешивающие размерности величин . Если с течением времени , то система асимптотически устойчива.

Устойчивость систем зависит от корней характеристического уравнения. Решение характеристического уравнения есть сумма экспоненциальных функций .

Рассмотрим варианты свободного движения систем от ненулевого начального положения при различных корнях характеристического уравнения (рисунок 7).

По рисунку 7 можно заметить, что для затухания переходного процесса и устойчивости линейной системы необходимо и достаточно, чтобы вещественные части корней были отрицательными, т.е. лежали слева от мнимой оси плоскости корней. Система будет находиться на границе устойчивости при наличии:

1) нулевого корня;

2) пары чисто мнимых корней;

3) бесконечного корня.

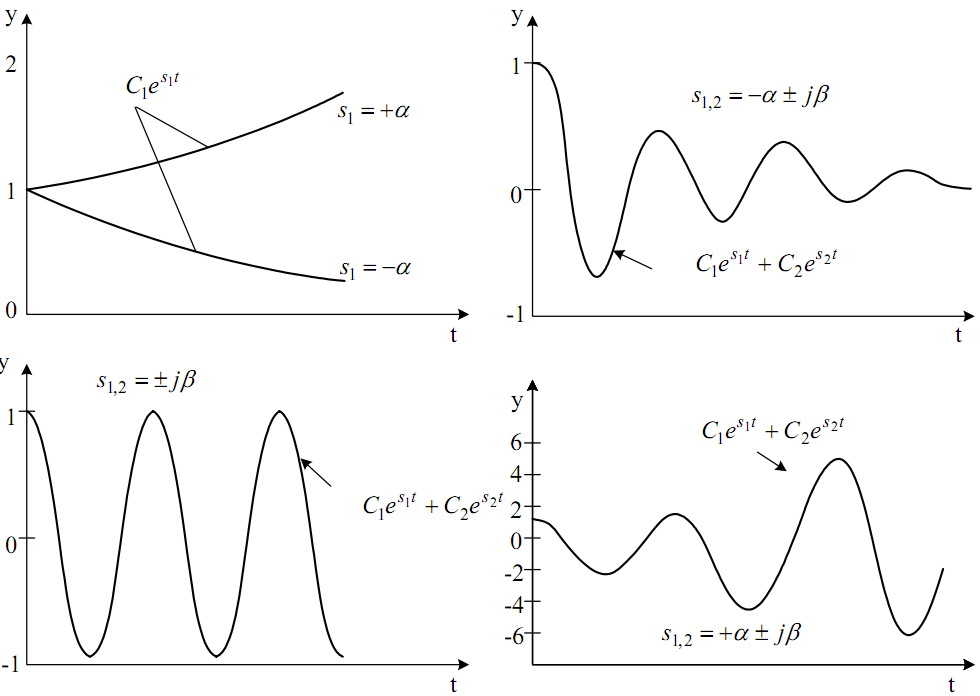
Рисунок 7. Графики движения систем при различных корнях характеристического уравнения

1.2. Критерий устойчивости Рауса-Гурвица

Критерий Рауса-Гурвица используется при анализе устойчивости линейных стационарных систем. Он позволяет аналитически определить, все ли корни полинома имеют отрицательные действительные части.

Вещественные части корней будут отрицательными в том случае, если все коэффициенты уравнения и диагональные миноры главного определителя будут положительными. Главный определитель составляется так, что по главной диагонали выписываются коэффициенты уравнения начиная с в возрастающем порядке до . От каждого коэффициента главной диагонали по вертикали вверх выписываются коэффициенты с возрастающими и вниз – с убывающими индексами. Места в матрице коэффициентов с индексами больше и меньше 0 заполняются нулями.

Рассмотрим выражение критерия Гурвица для характеристического уравнения третьего порядка .

Главный определитель .

Условие Гурвица .

Следовательно, система будет устойчивой, если все коэффициенты положительны и .

1.3. Критерий устойчивости Михайлова

Чтобы все корни характеристического уравнения имели отрицательные вещественные части, необходимо, чтобы после подстановки частоты в соответствующий характеристический полином полное приращение его фазы при изменении частоты от нуля до бесконечности составляло , где – степень полинома . При этом характеристический полином опишет в комплексной плоскости кривую – «годограф Михайлова».

Свойства годографа Михайлова:

1) годограф всегда спиралевиден;

2) при , годограф начинается с точки на вещественной оси;

3) годограф уходит в бесконечность при ;

4) при четном , годограф стремится к бесконечности параллельно вещественной оси; при – нечетном, годограф стремится к параллельно мнимой оси (рисунок 8).

Замкнутая система устойчива в том случае, если годограф Михайлова при изменении от до проходит в положительном направлении квадрантов комплекса плоскости, начиная свое движение от положительной вещественной полуоси, и при этом нигде не обращается в нуль.