Контрольная работа По вычислительной математике Вариант 60
Содержание
Задание 2. Метод наименьших квадратов 11
Задание 3. Интерполяция функций 15
Задание 4. Алгоритмы численного интегрирования функций 18
Список использованной литературы 23
Задача 1. Методы решения нелинейных уравнений
Решить уравнение методами итерации, Ньютона, хорд.
.
Составить схему уточнения корня. Получить программу на языке Quick Basic. Провести оценку погрешности результата.
Решение:
Составим функцию
Для
отделения корней функции
,
составим таблицу знаков:
Таблица 1
хi |
0 |
1 |
2 |
3 |
4 |
знак f(x) |
1 |
1 |
-1 |
1 |
1 |
На
отрезках
и
функция меняет знак, т.е. на каждом
отрезке существует по крайней мере один
корень.
Убедимся, что он единственный на этом отрезке:
,
,
Значит,
производная
- монотонно возрастающая функция.
Составим таблицу знаков производной на данном отрезке:
Таблица 2
хi |
0 |
1 |
2 |
3 |
4 |
Знак |
-1 |
-1 |
-1 |
1 |
1 |
При
функция
монотонно возрастает (
,
,
),
следовательно, отрезок
имеет единственный корень.
При
функция
монотонно убывает (
,
,
),
следовательно, отрезок
имеет единственный корень.
1. Метод Ньютона
Найдем корень на отрезке .
Достаточные условия сходимости метода Ньютона:
1.
непрерывна на
и
,
2.
и
отличны от нуля и сохраняют знак на
.
Условия выполняются.
Начальное приближение выбираем из условия
.
Так
как
,
то пусть
.
Рекуррентная формула:
,
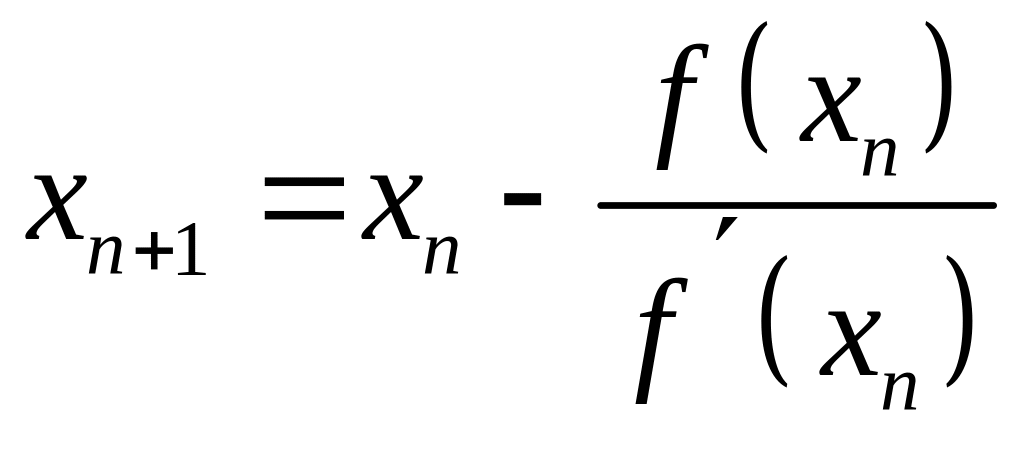n=0,
1 …
Оценка погрешности:
,
При этом условие окончания поиска корня при заданной точности Е:
,
и
- модули наибольшего и наименьшего
значений соответственно
и
.
Результаты решения представим в таблице:
Таблица 3
n |
x |
F(x) |
F'(x) |
f(x) |
0 |
1 |
1,080604612 |
-2,68294 |
-0,402768537 |
1 |
1,40277 |
0,09393044 |
-2,1663 |
-0,043359929 |
2 |
1,44613 |
0,001592499 |
-2,09222 |
-0,000761152 |
3 |
1,44689 |
0,000000507 |
-2,09089 |
-0,000000243 |
4 |
1,44689 |
0,000000000 |
-2,09089 |
0,000000000 |
-
уточненный корень на отрезке
.
Погрешность равна 0,000000243
.
Решение на языке Паскаль(newton.pas):
Результат:
2. Метод итерации.
На отрезке найдем корень методом итерации.
Достаточные условия сходимости:
дифференцируема
и имеет разные знаки на отрезке
,
.
Итерирующая
функция
обеспечивает условие сходимости
.
Правило
выбора параметра
:
,
.
Значит,
,
.
Следовательно,
,
пусть
Приближения к корню вычисляются по формуле:
.
Пусть ,
Условие окончания поиска корня:
Оценка погрешности:
,
,
.
Составим таблицу:
Таблица 4
n |
x |
F(x) |
f(x) |
0 |
1 |
1,080604612 |
1,540 |
1 |
1,54030 |
-0,187397134 |
1,447 |
2 |
1,44660 |
0,000598321 |
1,447 |
3 |
1,44690 |
-2,72614E-05 |
1,447 |
4 |
1,44689 |
1,23871E-06 |
1,447 |
5 |
1,44689 |
-5,62916E-08 |
1,447 |
- уточненный корень на отрезке .
Погрешность равна 1,295E-06
Решение на языке Паскаль (iteraz.pas):
Результат:
