2. Складання розрахункової схеми

Розробка математичної моделі гідромеханічного процесу починається з опису роботи модельованого елемента і складання розрахункової схеми із зазначенням всіх конструктивних параметрів.

d_c – діаметр сопла; d₁ – діаметр великого жорсткого центру

d₂ – діаметр малого жорсткого центру

D– діаметр затиснення мембрани; h – переміщення мембрани

Розрахункова схема представлена на (рис.2.2).

Рис.2.2 Розрахункова схема елементу, що реалізує логічну функцію "НІ" по дросельній схемі.

2.3. Складання математичної моделі

2.3.1. Математична модель складається: з пневматичної лінії, оскільки пневматична лінія коротка (набагато коротше довжини хвилі тиску) рівняння можна уявити в повних похідних, и пневматичну лінію розбити на 3 зосереджених параметри, тому лінію представляють у вигляді трьох елементів активного опору R, індуктивного опору L і ємкісного С. Для кожного складемо два рівняння, що зв'язують вхідні та вихідні сигнали.

При подачі вхідного сигналу , газ надходить в камеру А (рис.1), зв'язок тисків і можна отримати на підставі рівняння нерозривності, рівняння Бернуллі.

Рис. 2.3 Пневматична лінія

Початкові і граничні умови:

- для камери А.

де масові витрати

L- індуктивний опір;

;

Площа поперечного перетину ;

R- активний опір

;

С- ємнісний опір

;

a - швидкість звуку

;

Користуючись групою рівнянь, вказаних вище, отримуємо рівняння, що описує пневмолінію:

.

Передатна функція пневмолінії:

=

2. Складання рівнянь руху рухливих частин елемента, що модулюється

Рівняння руху операційного підсилювача складаємо на підставі загально фізичних законів: рівняння збереження енергії у вигляді балансу сил з урахуванням сил тертя діючих на рухливу частину операційного підсилювача.

,

де С – жорсткість пружини;

m– маса жорстких частин елементу;

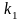- коефіцієнт тертя;

- ефективна площа.

Приводимо рівняння до безрозмірного виду:

.

Введемо заміну:

.

Так як ,

де - період власних недемпфованих коливань мембрани;

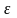- приведений коефіцієнт тертя.

Отримаємо:

.

Якщо , то:

.

Видповідно з теоріі коливань, знаходимо

,

де -маса рухливих частин.

Жорсткість мембрани знаходимо з умови, що при підвищенні тиску в камері А на 10мм водяного стовпа відбувається закриття сопла, що зв'язує камеру Б з атмосферою.

;

;

; d=0 ;

;

= -максимальне переміщення мембрани;

- жорсткість.

Маса рухливих частин рівна ,

але оскільки жорсткий центр в цьому елементі відсутній, то отримаємо наступне:

.

Знайдемо, коефіцієнт демпфування: = ;

період власних недемпфованих коливань.

де с - жорсткість пружини;

k - коефіцієнт тертя;

- коефіцієнт демпфування;

Передатна функція:

.

2.4. Складання рівнянь нерозривності проточних частин

Складаємо рівняння нерозривності для докритичного режиму витікання газу.

m₁₁=m₁₂ + m₁₃ ;m₁₁=₁ ((P_п – P_в) ; )

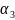
m₁₂ = ₂ (P_в; ;m₁₃ =₃ (  (P_в – Р_в)

2.5. Лініаризація математичної моделі.

Масова витрата скидається в атмосферу, а частина накопичується. Для отримання лінійної математичної моделі, що істотно полегшує виконання розрахунків, і аналізу отриманих даних виконуємо лініаризацію нелінійних членів математичної моделі:

m₁₁=K₁₁ +K₁₁₀

де m₁₁= ;

m₁₂=K₁₂ +K₁₂₀

де m₁₂= ;

Коефіцієнт витрати визначаємо по графіку залежності від відстані між соплом і заслінкою.

Передатна функція: .