
- •Східноукраїнський національний університет
- •Кафедра гідрогазодинаміки
- •Курсова робота
- •Луганськ - 2013 вступ
- •Актуальність роботи
- •Розділ 1 огляд існуючих конструкцій. Принципи дії математичної моделі процесів у гідромеханічних і пневматичних елементах
- •1.1 Одномембраннi пневмореле
- •1.2 Двохмембранні пневмoреле
- •1.3. Трьохмембранні пневмореле
- •1.4. Дросельні схеми
- •Висновки,мета і задачі дослідження
- •Розділ 2 розробка математичної моделі гідромеханічного процесу в елементі, що реалізує логічну функцію «ні» по дросельній схемі.
- •2.1. Принцип роботи пристрою елементу, що реалізує логічну функцію «ні» по дросельній схемі
- •Складання розрахункової схеми
- •2.3. Складання математичної моделі
- •Складання рівнянь руху рухливих частин елемента, що модулюється
- •2.4. Складання рівнянь нерозривності проточних частин
- •2.5. Лініаризація математичної моделі.
- •2.6 Визначення чисельних значень коефіцієнтів, що входять в математичну модель
- •Розділ 3
- •3.1 Дослідження динамічних характеристик модельованого елементу.
- •3.2 Складання структурної схеми
- •Висновок
- •Список літератури
- •3.3. Упрощенная модель динамических характеристик пневматических элементов нечеткой логики. Планирование эксперимента
- •Розділ 4 планування експерименту та оптимізація геометричних параметрів елемента, що моделюється
- •4.1. Оптимізація геометричних параметрів
- •4.2. Адекватність апроксимаційної моделі
- •4.3. Визначення типу поверхні за допомогою інваріантів
- •4.4. Визначення максимуму поверхні
- •4.5 Висновки до розділу 4
- •Висновки до виконаної роботи
- •Список літератури
4.4. Визначення максимуму поверхні
Максимум і мінімум функції декількох змінних
Визначення
1. Ми говоримо, що функція
 має
максимум в точці
має
максимум в точці
 (т.е. при
(т.е. при и
и
 ),
якщо
),
якщо
 ,
,
для
усіх точок
 ,
досить близьких до точки
,
досить близьких до точки
 і відрізняються від неї.
і відрізняються від неї.
Визначення 2. Вчинено аналогічно говорять, що функція має мінімум в точці , якщо
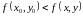
для усіх точок , досить близьких до точки і відрізняються від неї.
Максимум і мінімум функції називаються екстремумами функції, тобто кажуть, що функція має екстремум в даній точці, якщо функція має максимум чи мінімум в даній точці.
Дане вище визначення максимуму і мінімуму можна перефразувати в такий спосіб.
Покладемо ;
;
 ;
;
тоді
 .
.
1) якщо при всіх досить малих прирости незалежних
змінних, то функція
при всіх досить малих прирости незалежних
змінних, то функція
 досягає максимуму в точці
досягає максимуму в точці
 .
.
2) якщо при всіх досить малих прирости незалежних
змінних, то функція
досягає мінімуму в точці
.
при всіх досить малих прирости незалежних
змінних, то функція
досягає мінімуму в точці
.
Ці формули переносяться без зміни на функції будь-якого числа змінних.
Теорема 1. (Необхідні умови екстремуму).
Якщо
функція
досягає екстремуму при
,
,
то кожна приватна похідна першого
порядку від
 або звертається в нуль при цих значеннях
аргументів, або не існує.
або звертається в нуль при цих значеннях
аргументів, або не існує.
Ця теорема не є достатньою для дослідження питання про екстремальні значеннях функції, але дозволяє знаходити ці значення в тих випадках, в яких ми заздалегідь впевнені в існуванні максимуму або мінімуму.
Точки, в яких
 (або
не існують) и
(або
не існують) и
 (
або не існують), називаються критичними
точками функції
.
Якщо функція досягає екстремуму в
будь-якій точці, то (в силу теореми 1) це
може статися тільки в критичній точці.
(
або не існують), називаються критичними
точками функції
.
Якщо функція досягає екстремуму в
будь-якій точці, то (в силу теореми 1) це
може статися тільки в критичній точці.
Для дослідження функції в критичних точках встановимо достатні умови екстремуму функції двох змінних:
Теорема 2. Нехай в деякій області, яка містить точку , функція має безперервні приватні похідні до третього порядку включно, і нехай, крім того, точка є критичною точкою функції , т.е.
 ,
,
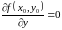 .
.
Тоді при , :
1) маємо максимум, якщо
 и
и
 .
.
2) маємо мінімум, якщо
і .
.
3) не має ні максимуму, ні мінімуму, якщо
 .
.
4) якщо ,
то екстремум може бути і може не бути
(в цьому випадку потрібно подальше
дослідження).
,
то екстремум може бути і може не бути
(в цьому випадку потрібно подальше
дослідження).
Дослідження функції на екстремум
Досліджуємо функцію на максимум
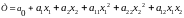 .
.
1) знайдемо критичні точки, користуючись необхідними умовами екстремуму:
 .
.
Звідси отримуємо дві критичні точки:
 ;
;
 ,
,
 ;
;
 .
.
2) знайдемо похідні другого порядку:
 ,
,
 ,
,
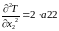 .
.
3) досліджуємо характер критичної точки
 ;
; ;
;
 ;
;
 ;
;
 .
.
Отже в досліджуваній області максимум не існує.
Максимум
(глобальний максимум) не існує. Накладаємо
обмеження
 (з графіка) тоді отримуємо функцію однієї
змінної
(з графіка) тоді отримуємо функцію однієї
змінної
,
 .
.
Її похідна завжди існує і скінченна
 .
.
Корінням похідної будуть
 ;
;
 .
.
Цим значенням весь
проміжок
 розбивається на наступні частини:
розбивається на наступні частини: ,
,
 .
.
Визначаємо знак похідної в цих проміжках:
в проміжку (-) (+)
(-) (+)
в проміжку (+) (+)
Звідси зрозуміло,
що при
 функція має максимум.
функція має максимум.
В точці
 функція
функція
 має
максимум.
має
максимум.
Максимальне значення на поверхні (рис.4.1.) Досягається в точці
x1 = - 0,5, x2 = - 1.41 ω=80 1/с. Максимальне значення є оптимальним значенням роботи пневматичного пристрою вибору максимуму.
