4.2. Адекватність апроксимаційної моделі

Одним зі способів визначення адекватності отриманої аппроксімаціонної моделі, крім критерію Фішера, є використання коефіцієнта кореляції. Коли дві змінні величини y_опі y_р залежать один від одного так, що кожному значенню однієї з них відповідають цілком визначені одне або кілька значень іншої, то між ними є функціональний зв'язок.

Іноді доводиться мати справу з такими змінними величинами, між якими існує залежність, але ця залежність не є цілком визначеною: кожному значенню однієї з величин (наприклад, y_р) відповідає деяка сукупність значень іншої (наприклад, y_оп). У цьому випадку зв'язок, який існує між змінними y_оп і y_р, називається кореляційним зв'язком.

Кореляційна зв'язок величин полягає в тому, що при завданні однієї з них встановлюється не одне точне значення, а ймовірності різних значень іншої. Таким чином, залежність виявляється не між самими величинами, а між кожною з них і відповідним їй математичним очікуванням іншого.

Кореляційна зв'язок встановлюється наоснові статистичних методів аналізу. Вона є проміжною між точної залежністю, що дається функціональним зв'язком, і досконалої незалежністю змінних.

Найбільш важливим показником зв'язку з цим служить коефіцієнт кор-реляції r, характеризує ступінь лінійної пов'язаностіy_опи y_р .

Абсолютна величина r завжди менше одиниці; коли вона дорівнює оди-ниці, y_опта y_р пов'язані функціональною лінійним зв'язком, коли r = 0, між y_оптаy_рлінійного кореляційного зв'язку не існує.

Коефіцієнт кореляції може бути визначений за такою формулою

Виконані розрахунки показали, що для даного випадок коефіцієнт кореляції дорівнює 0.92, що відчинить про адекватність апроксимаційний моделі та можливості її використання для оптимізації гідромеханічних характеристик досліджуваного елемента

4.3. Визначення типу поверхні за допомогою інваріантів

За допомогою інваріантів і семіінваріанта дамо необхідні ідостатні умови приналежності поверхні другого порядку до одного з п'яти типів.

Зауважимо, що поверхні III, IV і V типів характеризуються тим, що в їх найпростіших рівняннях відсутня мінлива х₃ домогтися цього можна тільки за рахунок повороту осей координат. Тому існує такий базис, що виникає з початкового поворотом, в якому загальне рівняння поверхностей III, IV і V типів має вигляд:

.

Тоді

.

Інваріантість отриманого визначника при паралельному перенесенні може бути доведена або безпосередньо, або так, як при паралельному перенесенні.

Для доказу твердження зауважимо аналогічно, що оскільки в найпростіших рівняннях поверхонь V типу відсутні х₂і х₃то існує базис, що виникає з початкового тільки поворотом.

Використовуючи раніше отримані коефіцієнти рівняння, знайдемо значення К₃:

.

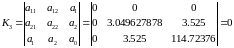Обчислимоінваріанти I₁, I₂, I₃, I₄:

I₁= a₁₁ + a₂₂ = = ,

I₂= ,

,

I₄ = K₃ =0.

Для визначення типу поверхні використовуємо наступну теорему:

Теорема. Для того щоб поверхня другого порядку належала I, II, III, IV або V типу, необхідно і достатньо виконання наступних ознак:

1. I₃ ≠ 0.

2. I₃=0, I₄ ≠ 0

3. I₃=0, I₄ = 0, I₂≠0.

4. I₃=0, I₄ = 0, I₂=0, K₃≠0.

5. I₃=0, I₄ = 0, I₂=0, K₃=0, I₁≠0.

Для визначення виду і назви поверхні скористаємося таблицею

Таблиця 4.3.

№ пп	Назва поверхні	Ознаки класу	Канонічне рівняння
Поверхность I типа, I3 ≠ 0.
1.	Еліпсоїд	I4< 0, I2 > 0, I1I3 > 0
2.	Уявний еліпсоїд	I4> 0, I2 > 0, I1I3 > 0
3.	Односмуговою гіперболоїд	I4> 0, I2 ≤ 0, чиI1I3 ≤ 0
4.	Двуполостний гіперболоїд	I4< 0, I2 ≤ 0, чи I1I3 ≤ 0
5.	Конус другу порядку	I4= 0, I2 ≤ 0, чи I1I3 ≤ 0
6.	Уявний конус	I4= 0, I2 ≤ 0, чи I1I3 ≤ 0

Продовження таблиці 4.3.

№ пп	Назва поверхні	Ознаки класу	Канонічне рівняння
Поверхня II типу, I3 = 0, I4 ≠ 0
7.	Еліптичніий параболоїд	I4< 0	(q > 0, p > 0)
8.	Гіперболічний параболоїд	I4> 0	(q > 0, p > 0)
Поверхня III типу, I3 = 0, I4 = 0, I2 ≠ 0
9.	Еліптичний циліндр	I2 > 0, I1K3 < 0
10.	Уявний еліптичний циліндр	I2 > 0, I1K3 > 0
11.	Гіперболічний циліндр	I2 < 0, K2≠ 0
12.	Дві пересічні площині	I2 < 0, K2 = 0
13.	Дві уявні пересічні площі	I2 > 0, K2 = 0
Поверхня IV типу, I3=0, I4 = 0, I2=0, K3≠0
14.	Параболічний циліндр	K3≠0
Поверхня V типу, I3=0, I4 = 0, I2=0, K3=0, I1≠0
15.	Дві паралельні площини	K2<0

Продовження таблиці 4.3.

16.	Дві уявні паралельні площини	K2>0
17.	Дві площі, що збігаються	K2= 0

Відзначимо, перш за все, що всі зазначені в таблиці ознаки є інваріантними щодо спільного перетворення системи координат, так як I₁, I₂, I₃, I₄ інваріантні при такому перетворенні, К₂ и K₃теж інваріантні при загальному перетворення для поверхонь тих типів, ознаки яких вони входять.

Таким чином, на підставі даних таблиці 4.3. у відповідності з отриманими значеннями інваріантів і семіінваріантов можна сказати, що отримана поверхня є поверхнею I типу і носить назву-двухполосний гіперболоід.