3. Особые точки и разложения в ряды

3. 1. Ряд Лорана

Теорема Лорана. Всякая функции аналитическая в кольце однозначно представляется в этом кольце в виде сходящегося ряда

, (3.1.1) где , - произвольное число, удовлетворяющее неравенству .

Степенной ряд (3.1.1) называется рядом Лорана функции или разложением в ряд Лорана функции по степеням . Здесь – фиксированная точка комплексной плоскости, называемая центром разложения.

Более подробно: ряд Лорана – это степенной ряд вида

.

Второе слагаемое называется правильной (регулярной) частью ряда Лорана, первое - главной частью ряда Лорана.

Замечание. Теорема Лорана останется в силе, если и функция аналитическая при , т.е. в окрестности бесконечно удаленной точки .

Чтобы разложить функцию в ряд Лорана в окрестности нужно выполнить замену переменной и провести разложение функции в ряд Лорана с центром в точке . Выполнив обратную замену переменной, получим искомый ряд Лорана в окрестности .

Пример 3.1.1. Разложить в ряд Лорана в окрестности .

Решение. Чтобы разложить функцию в ряд Лорана в окрестности нужно выполнить замену переменной и провести разложение функции в ряд Лорана с центром в точке . Выполнив обратную замену переменной, получим искомый ряд Лорана в окрестности .

Имеем по известному разложению. Ответ: .

Разложение в ряд Лорана рациональной функции

Разложение в ряд Лорана рациональной функции где и - многочлены и по степеням , проводится по схеме:

1. Если дробь неправильная, выделяем целую часть. Находим корни уравнения .

2. Точки являются особыми точками функции (в них не аналитична).

3. Разлагаем рациональную дробь на элементарные дроби, строим кольца аналитичности.

4. В каждом кольце аналитичности элементарные дроби разлагаем в ряды,

используя либо сумму геометрической прогрессии , либо

формулы , и почленное дифференцирование степенного ряда.

Замечание. Если необходимо разложить не по степеням , а по степеням , то заменой переменной можно свести к разложению в , а затем вернуться к исходной переменной.

П

Рис. 3.1.1.

ример 3.1.2. Найти все разложения функции в ряды Лорана по степеням .

Решение. Так как функция - это неправильная рациональная дробь, то от неправильной дроби перейдем к правильной, выделяя целую часть (так же как при интегрировании рациональных дробей).

Получим . Находим корни уравнения (в них не аналитична). Разложим знаменатель на простейшие множители: . Строим кольца аналитичности (см. рис. 3.1.1). Так как центр разложения , то необходимо сделать замену переменной с тем, чтобы свести к разложению в . Полагая , выполним замену переменной: . Разложение функции по степеням равносильно разложению по степеням . Так же как при интегрировании рациональных дробей правильную дробь представим в виде суммы элементарных дробей: . Имеем . Отсюда при получим равенство , при будем иметь: и, наконец, при : . Таким образом, нужно найти решение системы: Можно получить другую систему для нахождения коэффициентов из тождества . Решение в любом случае будет следующее: , , . Имеем

. (3.1.2)

К

Рис. 3.1.2.

ольца аналитичности функции (см. рис. 3.1.2) получаются из колец аналитичности смещением центра окружностей. В каждом кольце аналитичности по отдельности разложим по степеням дроби , , , а результат разложения подставим в равенство (3.1.2). Заметим, что . Поэтому для получения разложения достаточно разложить в каждом кольце аналитичности , затем почленно продифференцировать и умножить на . Мы используем искусственный прием для разложения рациональной дроби, а именно: сравнение с суммой геометрической прогрессии. Итак, в первой области, где , имеем: , , .

Из (3.1.2) следует, что при где

.

Поэтому .

В кольце разложение остается верным, так как . Для получения разложения преобразуем с тем, чтобы знаменатель геометрической прогрессии удовлетворял неравенству . В этом случае . Следовательно, . Для кольца

.

В области необходимо изменить разложение только одной дроби:

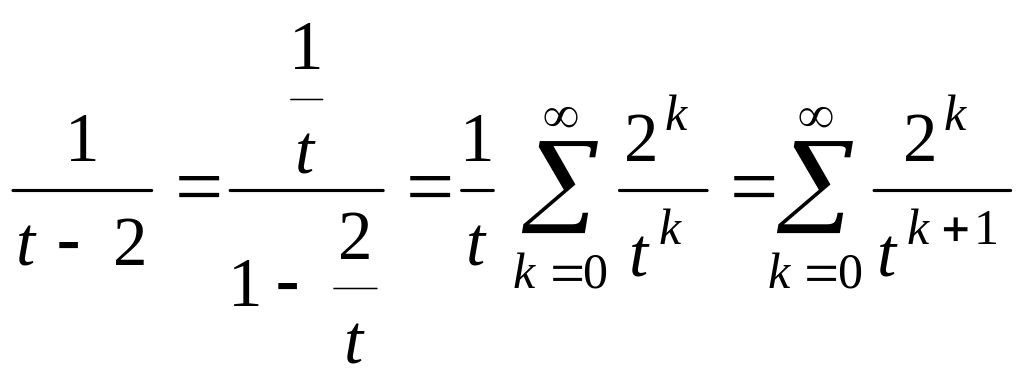. Поэтому разложение имеет вид:

.

Ответ: Если , то . Если , то . Если , то (см. рис. 3.1.1). 

Разложение в ряд Лорана с использованием разложений основных элементарных функций

Пример 3.1.3. Разложить в ряд Лорана по степеням .

Решение. Полагая и используя известное разложение , получим , .

Пример 3.1.4. Разложить в ряд Лорана в окрестности .

Решение. Чтобы разложить функцию в ряд Лорана в окрестности нужно выполнить замену переменной и провести разложение функции в ряд Лорана с центром в точке . Выполнив обратную замену переменной, получим искомый ряд Лорана в окрестности .

Имеем , так как по известному разложению .

.

7.0.1. Разложить в ряды Лорана заданные функции.

а) ; б) ; в) ,

г) ; д)

е) ж)

з) ; к) .

Ответы

7.0.1..а) б)

в) г)

д). e)

ж) з)

к)