2. Ряды

2.1. Сумма числового ряда. Признаки абсолютной сходимости

Конечные суммы называются частичными суммами ряда

. (2.1.1)

Числовой ряд (2.1.1) называется сходящимся, если сходится последовательность его частичных сумм . Предел последовательности частичных сумм называется суммой ряда .

Пример 2.1.1. Исследовать сходимость геометрической прогрессии:

.

Решение. Пусть обозначает -ую частичную сумму геометрической прогрессии, т.е. .

Следовательно, .

Отсюда и для частичной суммы геометрической прогрессии справедливо равенство:

.

Находим

Из определения сходящегося ряда следует, что геометрическая прогрессия сходится тогда и только тогда, когда и ее сумма, в этом случае, равна .

Пример 2.1.2. Исследовать сходимость ряда .

Решение. Данный ряд - геометрическая прогрессия, знаменатель которой

.

Следовательно, как следует из примера (2.1.1) ряд сходится. 

Необходимое условие сходимости ряда

Если сходится, то .

Пример 2.1.3. Исследовать сходимость ряда .

Решение. Для применения необходимого условия сходимости преобразуем модуль .

Отсюда по второму замечательному пределу . Поэтому не выполнено необходимое условие сходимости и ряд расходится. 

Первый признак сравнения

Пусть , и в числовом ряду (2.1.1). Тогда

1. если ряд сходится, то сходится и ряд ;

2. если же расходится ряд , то расходится и ряд .

Пример 2.1.4. Исследовать сходимость ряда .

Решение. Как показано в примере (2.1.2) ряд сходится. Кроме того, имеет место неравенство при всех . Так как исследуемый ряд “меньше” сходящегося ряда, то он также сходится.

Предельный признак сравнения

Пусть , и , . Тогда ряды и равносильны относительно сходимости.

Пример 2.1.5. Пусть произвольно задано. Исследовать по предельному признаку сходимость ряда .

Решение. Как известно, гармонический ряд расходится (см. пример 2.1.10). Поэтому по предельному признаку сравнения расходится ряд , так как .

Признак Даламбера абсолютной сходимости

Пусть - ряд с положительными членами >0 и , тогда

1. В случае ряд сходится,

2. В случае ряд расходится и не выполнено необходимое условие сходимости,

3. В случае ничего сказать нельзя.

Пример 2.1.6. Исследовать сходимость ряда .

Решение. Исследуем сходимость по признаку Даламбера, а именно, найдем

.

Следовательно, по признаку Даламбера ряд сходится.

Признак Коши абсолютной сходимости рядов

Признак Коши (радикальный). Пусть — ряд с неотрицательными членами и , тогда

1) в случае ряд сходится,

2) в случае ряд расходится и не выполнено необходимое условие сходимости,

3) в случае вопрос остается открытым.

Пример 2.1.7. Исследовать сходимость ряда .

Решение. Для применения признака Коши преобразуем модуль

.

Отсюда

.

Поэтому по признаку Коши ряд сходится абсолютно. 

Пример 2.1.8. Исследовать сходимость ряда .

Решение. Для применения признака Коши преобразуем модуль

.

Отсюда

.

Поэтому по признаку Коши не выполнено необходимое условие сходимости, а, следовательно, ряд расходится. 

Интегральный признак Коши

Если функция и (монотонно убывает) при всех , то ряд сходится тогда и только тогда, когда сходится несобственный интеграл .

Пример 2.1.9. Исследовать по интегральному признаку сходимость ряда Дирихле.

Решение. Рядом Дирихле называется ряд вида . Так как при всех и , то исследуем сходимость по интегральному признаку сходимости. Вычисляем

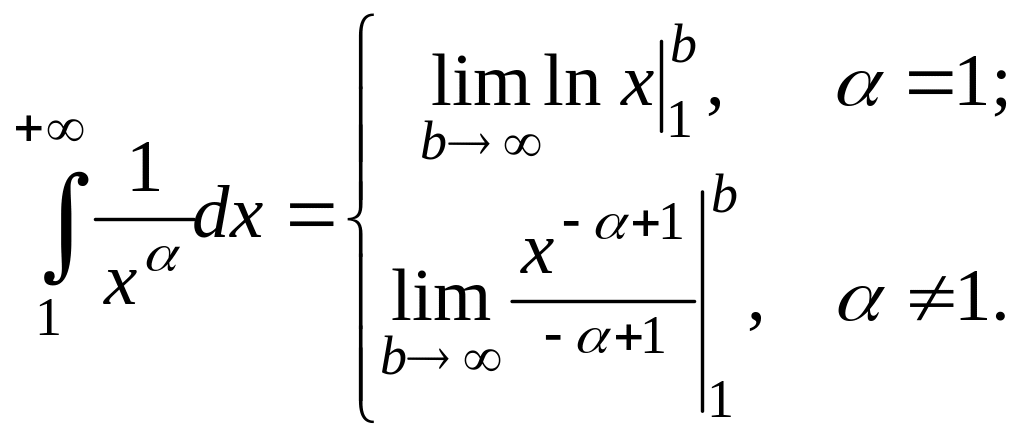
Отсюда

Соответственно, 

Ряд Дирихле сходится, если и расходится, если .

Пример 2.1.10. Исследовать сходимость гармонического ряда .

Решение. Гармонический ряд - это частный случай ряда Дирихле с . Поэтому ряд расходится.

Пример 2.1.11. Исследовать сходимость ряда .

Решение. Ряд - это частный случай ряда Дирихле с . Поэтому ряд сходится.

4.0.1. Доказать, что .

Указание. Ввести функцию y=f(x)=x^1/x и найти .

Замечание. Этот предел часто используется при исследовании сходимости числового ряда с помощью признака Коши.

4.0.2. Доказать, что .

Указание. Исследовать сходимость ряда с общим членом aⁿ/n! и применить необходимое условие сходимости числового ряда.

В задачах 4.0.3. – 4.0.17 исследовать сходимость числового ряда с общим членом u_n .

4.0.3. u_n= n²/3ⁿ . 4.0.4. u_n= n!/(2n)ⁿ . 4.0.5. u_n= ((n+1)/(3n-2))²ⁿ

4.0.6. u_n=(aⁿn!)/nⁿ, a>0. 4.0.7. u_n=(1+1/n)^m/aⁿ, m=n²,а>0. 4.0.8. u_n= 1/n^p. 4.0.9. u_n=1/(n∙ln^pn) . 4.0.10.u_n=1/lnⁿ(n+1). 4.0.11. u_n=1/(n∙lnn∙(lnlnn)^α ). 4.0.12. u_n=n²/sin(π/2ⁿ). 4.0.13. u_n= lnn/(n²+2). 4.0.14. u_n=arctgn/(n²+1). 4.0.15. u_n=nⁿ/(n!)². 4.0.16. u_n= (n/(2ⁿ + 1))ⁿ. 4.0.17. u_n=arcsinⁿ(1/n).

Ответы

4.0.3. Сходится. 4.0.4. Сходится. 4.0.5. Сходится. 4.0.6. Сходится при а<e. 4.0.7. Сходится при a>e. 4.0.8. Сходится при p>1. 4.0.9. Сходится при р>1. 4.0.10. Сходится. 4.0.11. Сходится при α>1. 4.0.12. Сходится. 4.0.13. Сходится. 4.0.14. Сходится. 4.0.15. Сходится. 4.0.16. Сходится. 4.0.17. Сходится.