
- •Содержание
- •1. Основные понятия теории функций комплексной переменной
- •1.1. Комплексные числа. Основные элементарные функции комплексной переменной
- •1. 2. Условия Коши – Римана. Аналитические функции
- •1.3. Интеграл от функции комплексной переменной
- •2. Ряды
- •2.1. Сумма числового ряда. Признаки абсолютной сходимости
- •В случае ряд сходится,
- •В случае ряд расходится и не выполнено необходимое условие сходимости,
- •В случае ничего сказать нельзя.
- •2.2. Условная сходимость
- •2.3. Функциональные ряды
- •3. Особые точки и разложения в ряды
- •3.2. Классификация изолированных особых точек
- •4. Теория вычетов
- •4.1. Вычет
- •4.2. Применение вычетов к вычислению интегралов
- •5. Элементы операционного исчисления
- •5.1. Понятие оригинала и изображения
- •Теорема разложения:
- •5.2. Восстановление оригинала по изображению
- •1. Линейные дифференциальные уравнения
- •2. Системы обыкновенных дифференциальных уравнений
1.3. Интеграл от функции комплексной переменной
Пусть дуга
![]() направленной кусочно-гладкой кривой
задана параметрическим уравнением
направленной кусочно-гладкой кривой
задана параметрическим уравнением
![]() .
Пусть
.
Пусть
![]() -
начальная точка и
-
начальная точка и
![]() -
конечная точка дуги. Тогда
-
конечная точка дуги. Тогда
 .
.
Пример 1.3.1. Вычислить
![]() ,
где
-
отрезок прямой от точки
,
где
-
отрезок прямой от точки
![]() до
точки
до
точки
![]() .
.
Решение.
Параметрическое задание отрезка:
![]() с
с
![]() .
Отсюда
.
Отсюда
![]() ,
,
![]() .
.
![]() .
.
Пример 1.3.2.
Вычислить
![]() ,
где
-
любое целое число.
,
где
-
любое целое число.
Решение. Поскольку
дуга – это окружность, целесообразно
следующее параметрическое задание
![]() ,
,
![]() .
.
Поэтому

Так как
![]() ,
то окончательно получим
,
то окончательно получим
![]()
Замечание. Значение
интеграла
![]() не зависит от
не зависит от
![]() .
.
Если функция
![]() является
аналитической в односвязной области,
где расположена дуга
,
то существует первообразная
является
аналитической в односвязной области,
где расположена дуга
,
то существует первообразная
![]() функции
,
т.е.
функции
,
т.е.![]() .
В этом случае справедлива формула
Ньютона - Лейбница
.
В этом случае справедлива формула
Ньютона - Лейбница
![]() ,
где
,
,
где
,
![]() - начальная и конечная точки дуги
соответственно.
- начальная и конечная точки дуги
соответственно.
Пример 1.3.3. Вычислить
![]() ,
где
-
отрезок прямой от точки
до
точки
.
,
где
-
отрезок прямой от точки
до
точки
.
Решение. Функция
![]() является аналитической функцией с
первообразной
является аналитической функцией с
первообразной
![]() .
Поэтому воспользуемся формулой Ньютона
-Лейбница
.
Поэтому воспользуемся формулой Ньютона
-Лейбница
![]() .
.
Теорема Коши
для односвязной области.
Если
- аналитическая функция в односвязной
области
,
а
![]() - замкнутый контур в
,
то
- замкнутый контур в
,
то
![]() .
.
Пример 1.3.4.
Вычислить
![]() .
.
Решение. Заметим,
что функция
![]() - аналитическая на всей комплексной
плоскости. Поэтому в силу теоремы Коши
для односвязной области этот интеграл
равен нулю.
- аналитическая на всей комплексной
плоскости. Поэтому в силу теоремы Коши
для односвязной области этот интеграл
равен нулю.
Интегральная формула Коши для односвязной области
Пусть - аналитическая функция в односвязной области . Пусть точка , - простой замкнутый контур в , охватывающий точку . Тогда
![]() .
.
Пример 1.3.5.
Вычислить интеграл
 .
.
Решение. Функция
![]() - аналитическая на всей комплексной
плоскости. Поэтому по интегральной
формуле Коши интеграл равен
- аналитическая на всей комплексной
плоскости. Поэтому по интегральной
формуле Коши интеграл равен
![]() .
.
3.0.1.
Пусть однозначная функция
определена и непрерывна в
области
и
![]() -
кусочно- гладкая ориентированная
кривая, лежащая в
.
-
кусочно- гладкая ориентированная
кривая, лежащая в
.
Пусть
,
![]() ,
где
,
- действительные функции переменных
и
.
Доказать, что вычисление интеграла
от функции
комплексной переменной
сводится к вычислению криволинейных
интегралов:
,
где
,
- действительные функции переменных
и
.
Доказать, что вычисление интеграла
от функции
комплексной переменной
сводится к вычислению криволинейных
интегралов:
![]() .
.
3.0.2.
Докажите,
что если
функция f(z)
– однозначная, аналитическая в
многосвязной области G
с границей
![]() и внутренними контурами
и внутренними контурами
![]() и непрерывна в замкнутой области
и непрерывна в замкнутой области
![]() ,
тогда имеет место равенство:
,
тогда имеет место равенство:
![]() ,
где
,
где
![]() ,
,
или
 .
.
(Теорема Коши для многосвязных областей).
Указание. Путем построения вспомогательных линий свести к случаю односвязной области.
3.0.3. С помощью интегральной формулы Коши вычислить интегралы.
а)
 ; б)
; б)
 ; в)
; в)
![]() ;
;
г)
![]() ; д)
; д)
 ; е)
; е)
 .
.
ж)
![]() ; з)
; з)
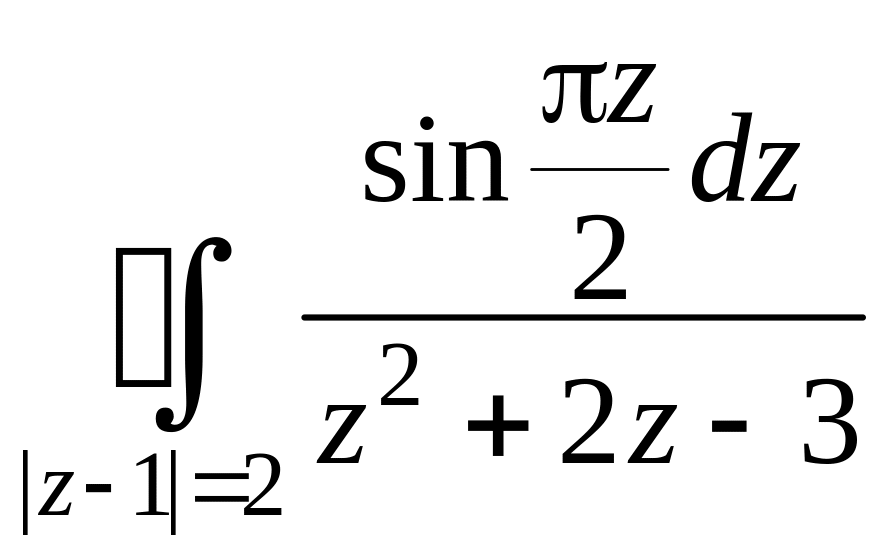 ; и)
; и)
![]() ;
;
к)
![]() ; л)
; л)
 ; м)
; м)
![]() ;
;
н)
![]() ; о)
; о)
 ; п)
; п)
 ;
;
р)
 ; с)
; с)
 ; т)
; т)
 .
.
Вычислить
 ,
где Г – отрезок, соединяющий точки
,
где Г – отрезок, соединяющий точки
 .
.
3.0.5.
Вычислить
![]() ,
где
-
дуга окружности
,
где
-
дуга окружности
![]() ,
,
![]() .
.
В задачах 3.0.6
– 3.0.13
вычислить интеграл
![]() .
.
3.0.6. Функция f(z) = y + xi , С - ломаная линия ОАВ с вершинами в
точках zO= 0 , zA= i , zB= 1 + i .
3.0.7. Функция f(z) = z2 , C=AB – отрезок прямой, соединяющий точки
zA = 1 и zB = i .
3.0.8. Функция f(z) = x – yi , С – замкнутый контур | z | = 1.
3.0.9. Функция f(z)= (1-2x) + i(1+2y) , C=AB - линия соединяющая точ- ки А и В ( zA=0 , zB= 1 + i ) а) по прямой, б) по параболе у = х2 , в) по ломаной AMB, где zM=1 .
3.0.10.
Функция f(z)
= zImz2
, где
-
дуга окружности
,
![]() .
.
3.0.11. Функция f(z) = zRez , C - | z | = 1 , обход в положительном на правлении.
3.0.12.
Функция f(z)=Rez,
C=AB
– линия соединяющая точки А и В (![]() ,
,
![]() )
: а) по прямой , б) по ломаной АМВ ,
где zM
= 2 .
)
: а) по прямой , б) по ломаной АМВ ,
где zM
= 2 .
3.0.13. Функция f(z) = ez , C=AB ( zA = 0 , zB = 1+ i ) а) дуга параболы y = x 2 , б) отрезок прямой.
Ответы
3.0.3.
а)![]() б)
б)![]() в)0; г)
в)0; г)![]() д)
д)![]() е)
е)![]() ж)
ж)![]() з)
з)![]() и)
и)![]() к)
к)![]() л)
м)
л)
м)![]() н)
н)![]() о)0; п)0; р)
о)0; п)0; р)![]() с)
с)![]() т)
т)![]() 3.0.4.
1; 3.0.5.
3.0.4.
1; 3.0.5.
![]() ;
3.0.6.
1 + i;
3.0.7.
–(1+i)/3;
3.0.8.
2πi;
3.0.9.
a)
2(i-1) ; б)
-2 + 4i/3; в)-2
;
3.0.10.
–π/2;
3.0.11.
0;
3.0.12.
а)
2 + i ; б)6
+ 2i; 3.0.13.
а)
ecos1 – 1 + iesin1; б)
ecos1 – 1 + iesin1.
;
3.0.6.
1 + i;
3.0.7.
–(1+i)/3;
3.0.8.
2πi;
3.0.9.
a)
2(i-1) ; б)
-2 + 4i/3; в)-2
;
3.0.10.
–π/2;
3.0.11.
0;
3.0.12.
а)
2 + i ; б)6
+ 2i; 3.0.13.
а)
ecos1 – 1 + iesin1; б)
ecos1 – 1 + iesin1.
