
- •Содержание
- •1. Основные понятия теории функций комплексной переменной
- •1.1. Комплексные числа. Основные элементарные функции комплексной переменной
- •1. 2. Условия Коши – Римана. Аналитические функции
- •1.3. Интеграл от функции комплексной переменной
- •2. Ряды
- •2.1. Сумма числового ряда. Признаки абсолютной сходимости
- •В случае ряд сходится,
- •В случае ряд расходится и не выполнено необходимое условие сходимости,
- •В случае ничего сказать нельзя.
- •2.2. Условная сходимость
- •2.3. Функциональные ряды
- •3. Особые точки и разложения в ряды
- •3.2. Классификация изолированных особых точек
- •4. Теория вычетов
- •4.1. Вычет
- •4.2. Применение вычетов к вычислению интегралов
- •5. Элементы операционного исчисления
- •5.1. Понятие оригинала и изображения
- •Теорема разложения:
- •5.2. Восстановление оригинала по изображению
- •1. Линейные дифференциальные уравнения
- •2. Системы обыкновенных дифференциальных уравнений
1. Основные понятия теории функций комплексной переменной
1.1. Комплексные числа. Основные элементарные функции комплексной переменной
Комплексным
числом
называется пара
действительных чисел
![]() и
и
![]() взятых в определенном порядке
взятых в определенном порядке
![]() ,
,
![]() (real)-
действительная
часть,
(real)-
действительная
часть,
![]() (imaginary)-
мнимая часть.
Однако, для простоты восприятия действий
с комплексными числами, здесь не
принимается во внимание аксиоматический
подход к понятию комплексного числа и
рассматривается комплексное число
как алгебраическое выражение
(imaginary)-
мнимая часть.
Однако, для простоты восприятия действий
с комплексными числами, здесь не
принимается во внимание аксиоматический
подход к понятию комплексного числа и
рассматривается комплексное число
как алгебраическое выражение
![]() с буквой
с буквой
![]() ,
учитывая при этом, что
,
учитывая при этом, что
![]() .
.
Пример 1.1.1. Найти
![]() ,
,
![]() ,
если
,
если
![]() ,
,
![]() .
.
Решение. Вычисляем
![]() ,
,
![]() .
.
Равенство двух комплексных чисел означает равенство их действительных и мнимых частей.
Модуль
комплексного числа
находится
по формуле
![]() .
Каждому комплексному числу соответствует
в декартовой системе координат на
плоскости точка с координатами
.
Каждому комплексному числу соответствует
в декартовой системе координат на
плоскости точка с координатами
![]() ,
,
![]() (см. рис. 1.1.1). Также, для простоты
восприятия действий с комплексными
числами понятие модуля комплексного
числа рекомендуется связать с теоремой
Пифагора (см. рис. 1.1.1).
(см. рис. 1.1.1). Также, для простоты
восприятия действий с комплексными
числами понятие модуля комплексного
числа рекомендуется связать с теоремой
Пифагора (см. рис. 1.1.1).
Пример 1.1.2. Найти
![]() ,
если
,
если
![]() .
.
Решение. Так как
![]() ,
,
![]() ,
то
,
то
![]() .
.
Из геометрической интерпретации комплексных чисел следуют ряд полезных выводов и неравенств:
1)
![]() .
.
2)
![]() – расстояние между точками
– расстояние между точками
![]() и
и
![]() .
.
3)
![]() .
.
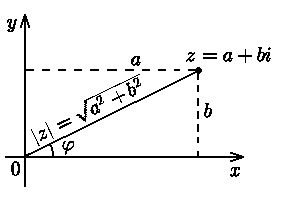
Из геометрического
изображения комплексного числа (см.
рис. 1.1.1) также следует, что угол
![]() ,
определяемый как главное
значение аргумента
,
определяемый как главное
значение аргумента
![]() ,
находится
по формуле:
,
находится
по формуле:
Рис. 1.1.1.
(для
числа
![]() аргумент не определен). Из прямоугольного
треугольника (см. рис. 1.1.1) получается
равенство
аргумент не определен). Из прямоугольного
треугольника (см. рис. 1.1.1) получается
равенство
![]() ,
называемое тригонометрической
формой
,
называемое тригонометрической
формой
![]() .
Из
тригонометрической формы записи и
формулы Эйлера
.
Из
тригонометрической формы записи и
формулы Эйлера
![]() следует
показательная форма записи
комплексного числа:
следует
показательная форма записи
комплексного числа:
![]() .
Если
.
Если
![]() пробегает
множество всех целых чисел, то получаем
многозначную
функцию
пробегает
множество всех целых чисел, то получаем
многозначную
функцию
![]()
Пример 1.1.3. Найти модули и главные значения аргументов следующих чисел –2+2i; –1; 3+4i и записать тригонометрическую форму этих чисел.
Решение. Воспользуемся
формулой для
![]() .
В первом случае x=
–2, y =2,
точка z=–2+2i
лежит во второй четверти
.
В первом случае x=
–2, y =2,
точка z=–2+2i
лежит во второй четверти
![]() .
Найдем модуль этого числа
.
Найдем модуль этого числа
![]() ,
поэтому
,
поэтому
![]() .
Во втором случае x= –1,
y=0,
.
Во втором случае x= –1,
y=0,
![]() ,
поэтому
,
поэтому
![]() .
В третьем случае x=3,
y=4
, отсюда имеем
.
В третьем случае x=3,
y=4
, отсюда имеем
![]() ,
так как
,
так как
![]() ,
то
тригонометрическая форма числа 3+4i
записывается в виде
,
то
тригонометрическая форма числа 3+4i
записывается в виде
![]()
Пример 1.1.4. Записать
тригонометрическую и показательную
формы записи для чисел:
![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() .
.
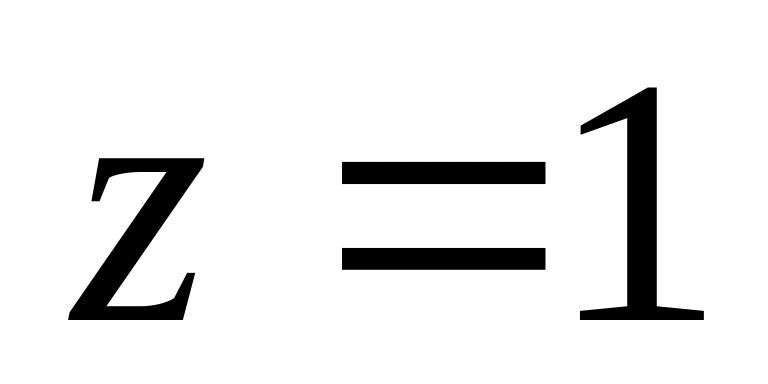 :
:
 ,
,
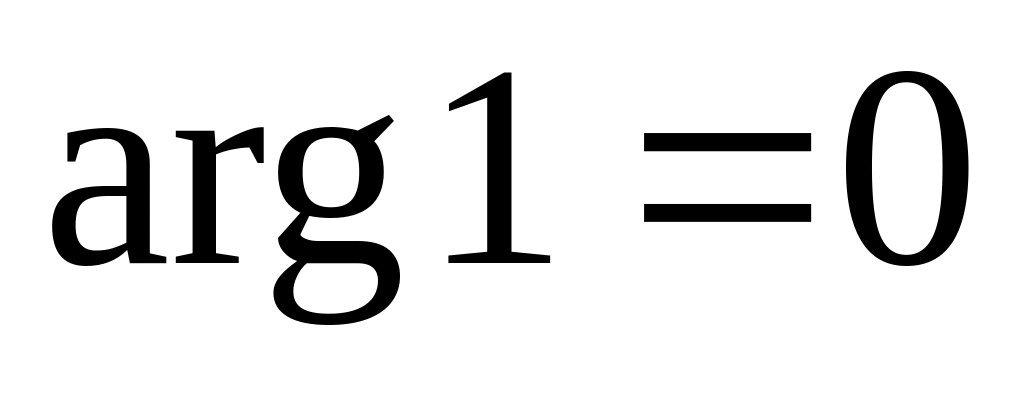 ;
;
 ;
;
 :
: ,
,
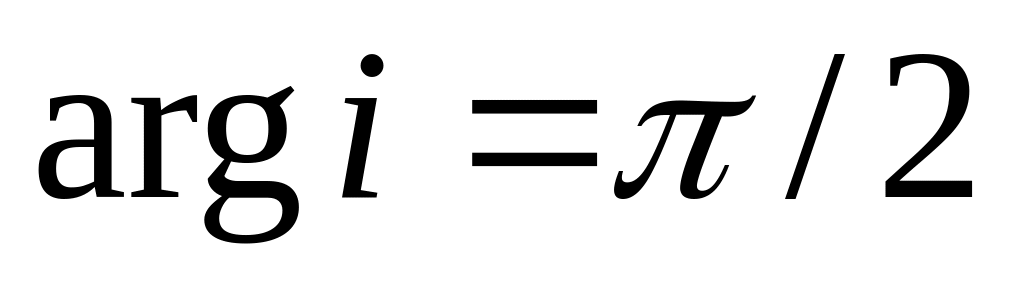 ;
;
 ;
; :
: ,
,
 ;
;
 ;
; :
:
 ,
,
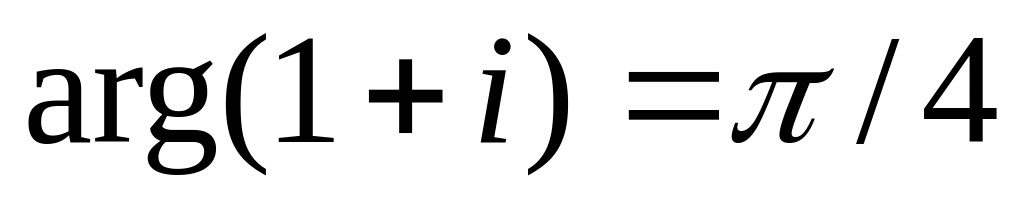 ;
;
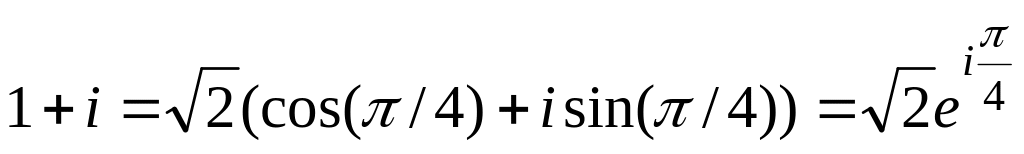 ;
;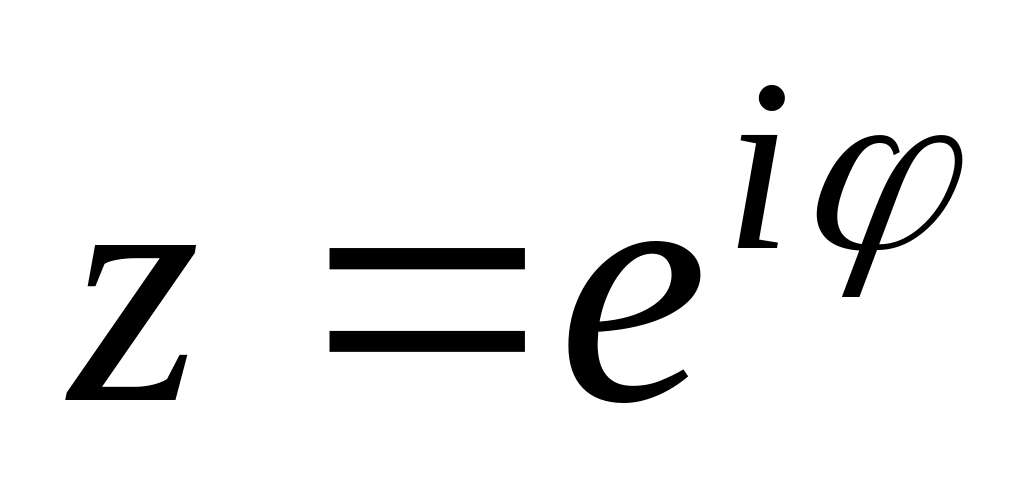 :
:
 ;
;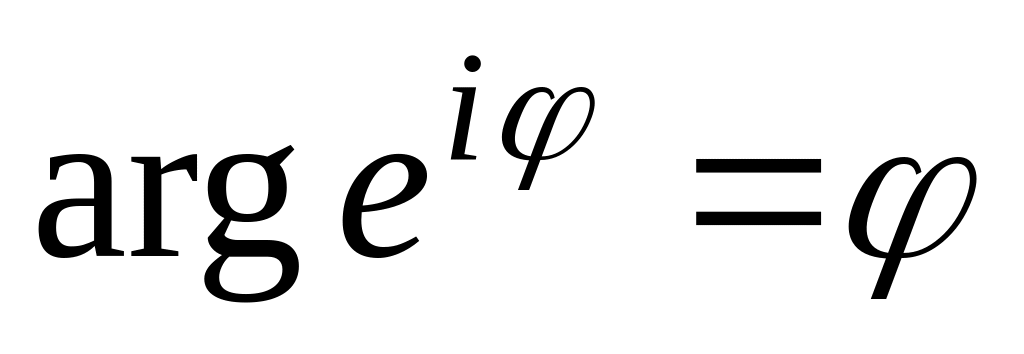 ;
;
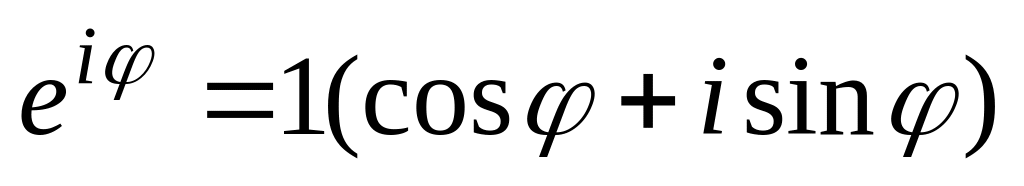 .
.
Функция
![]() обладает свойствами
показательной функции,
например,
обладает свойствами
показательной функции,
например,
![]() ,
, ![]() ,
, ![]() .
.
Учитывая это, находим формулу извлечения целого корня:
![]() .
(1.1.1)
.
(1.1.1)
Таким образом,
корень
![]() -
ой степени имеет
различных значений, которые получаются
подстановкой
-
ой степени имеет
различных значений, которые получаются
подстановкой
![]() и функция
и функция
![]() является многозначной.
является многозначной.
Пример 1.1.5. Найти
все значения корня
![]() .
.
Р
Рис. 1.1.2.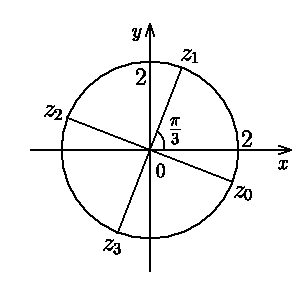
![]() :
:
![]() ;
;
![]() .
По формуле (1.1.1)
.
По формуле (1.1.1)
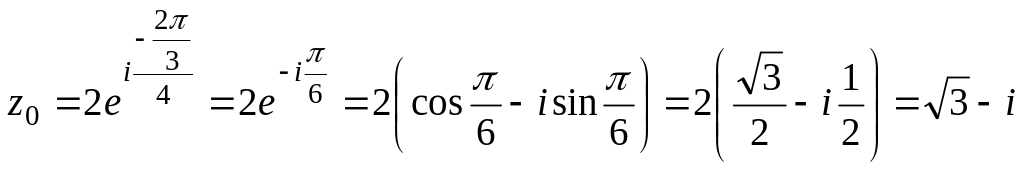 ;
; ;
;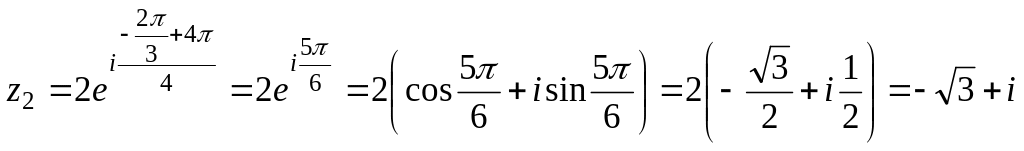 ;
; (см.
рис. 1.1.2).
(см.
рис. 1.1.2).
Заметим, что всякий
ответ доводится до алгебраической
формы записи комплексного числа
![]() ,
если не оговорено обратное.
,
если не оговорено обратное.
Комплексное
сопряженное
к числу
называется число
![]() ,
обозначаемое также как
,
обозначаемое также как
![]() .
.
Пример 1.1.6. Для
произвольного числа
найти
![]() .
.
Решение.
![]() .
.
Пример 1.1.7. Найти (2+i)/(1+2i); 1/i.
Решение. (2+i)/(1+2i)= (2+i)(1-2i)/(1+4)=0.8-0.6i; 1/i = -i.
Рис. 1.1.3.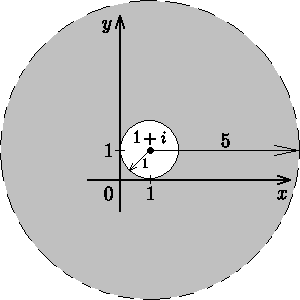
1)
![]() . 2)
. 2)
![]() .
.
3) При умножении двух комплексных чисел их модули перемножаются (растяжение или сжатие), а аргументы складываются (поворот на плоскости).
4) При делении двух комплексных чисел их модули делятся (модуль знаменателя 0), а аргументы вычитаются.
Сделаем еще важное замечание о том, что комплексные числа нельзя сравнивать. Действительно, два радиус-вектора, соответствующих изображению комплексных чисел на плоскости, можно только сравнить по длине, т.е. комплексные числа сравнимы по модулю.
Пример 1.1.8.
Изобразить на плоскости множество
точек
,
для которых справедливо неравенство
![]() .
.
Решение. Вычисляем
модули:
![]() ,
,
![]() .
Следовательно, комплексные числа
удовлетворяют неравенству:
.
Следовательно, комплексные числа
удовлетворяют неравенству:
![]() .
Строим окружности с центром в точке
.
Строим окружности с центром в точке
![]() и радиусами
и радиусами
![]() и
и
![]() ,
соответственно. Множество точек
,
удовлетворяющих неравенству
,
изображается в виде кольца (см. рис.
1.1.3).
,
соответственно. Множество точек
,
удовлетворяющих неравенству
,
изображается в виде кольца (см. рис.
1.1.3).
Простейшие множества точек на комплексной плоскости:
а) |z-z0|=a (a>0) - окружность с центром в точке z0 радиуса a;
б) |z-z0|<a (a>0) - открытый круг с центром в точке z0 радиуса a;
в) |z-z0|>a (a>0) - внешность открытого круг с центром в точке z0 радиуса a;
г) a<|z-z0 |<b (0<a<b) - открытое кольцо с центром в точке z0;
д) arg(z-z0)= - луч, с началом в точке z0 , идущий под углом к положительному направлению действительной оси.
е)
![]() <arg(z-z0)<
<arg(z-z0)<![]() - внутренность неограниченного открытого
сектора с вершиной в точке z0
и углом
раствора
- внутренность неограниченного открытого
сектора с вершиной в точке z0
и углом
раствора
![]() .
.
ж) Re z= a - прямая, параллельная мнимой оси, проходящая через точку (a,0);
з) Im z= b - прямая, параллельная действительной оси, проходящая через точку (0,b).
Основные элементарные функции комплексной переменной
1) Показательная
функция (формула Эйлера)
![]() .
.
2) Тригонометрические функции
![]()
![]()
![]()
![]() .
.
3) Гиперболические функции
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
Заметим, что
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
4) Логарифмическая
функция
![]() является многозначной функцией. Главное
значение (главная ветвь)
является многозначной функцией. Главное
значение (главная ветвь)
![]() .
.
5) Степенная
функция
![]() ;
главная ветвь
;
главная ветвь
![]() .
.
6) Показательная
функция![]() ;
главная ветвь
;
главная ветвь
![]() .
.
7) Обратные тригонометрические функции
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
(Ареасинус)
![]() ;
(Ареакосинус)
;
(Ареакосинус)
![]() ;
(Ареатангенс)
;
(Ареатангенс)
![]() ;
(Ареакотангенс)
;
(Ареакотангенс)
![]() .
.
Замечание. Функция
![]() комплексной переменной
сама является многозначной функцией.
Выбор ветви многозначной функции
здесь
производится из условия, чтобы
рассматриваемая функция
комплексной переменной
сама является многозначной функцией.
Выбор ветви многозначной функции
здесь
производится из условия, чтобы
рассматриваемая функция
![]() являлась аналитическим продолжением
соответствующей функции действительной
переменной. Из последнего условия
следует, что должно быть взято то
значение корня, которое положительно
при положительных действительных
значениях подкоренного выражения.
являлась аналитическим продолжением
соответствующей функции действительной
переменной. Из последнего условия
следует, что должно быть взято то
значение корня, которое положительно
при положительных действительных
значениях подкоренного выражения.
Пример 1.1.9. Найти
аналитическое выражение для функции
![]() .
.
Решение. По
определению обратной тригонометрической
функции равенство![]() равносильно равенству
равносильно равенству![]() .
Отсюда
.
Отсюда
![]() .
Полагая в последнем равенстве
.
Полагая в последнем равенстве
![]() ,
получим квадратное уравнение
,
получим квадратное уравнение
![]() .
Выбираем одно решение этого уравнения
(см. замечание)
.
Выбираем одно решение этого уравнения
(см. замечание)
![]() .
Следовательно,
.
Следовательно,
![]() и
и
![]() .
Так как
.
Так как
![]() ,
то
,
то
![]() .
.
Пример 1.1.10.
Вычислить
![]() .
.
Решение. Полагая
![]() ,
,
![]() ,
по формуле
находим
,
по формуле
находим
![]() .
.
По формуле
![]() ,
учитывая, что
,
учитывая, что
![]() ,
,
![]() ,
вычисляем
,
вычисляем
![]() ,
-
целое число. Отсюда
,
-
целое число. Отсюда
![]() .
.
1.0.1. Найти модуль и главное значение аргумента комплексных чисел:
а) z =1–i, б)
z=![]() ,
в) z= –3i,
г) z= – 4– 3i.
,
в) z= –3i,
г) z= – 4– 3i.
1.0.2. Заданные комплексные числа представить в тригонометрической и показательной формах:
а)
z = –
4, б)
z = 2i, в)
z = –2i, г)![]() ,
,
д) z =5+3i, е) z = –2–3i.
1.0.3. Вычислить:
а)
![]() ;б)
;б)
![]() ; в)
; в)
![]() ; г)
; г)![]() ;д)
;д)
![]() .
.
1.0.4. Найти все значения корня:
а)
![]() ; б)
; б)
![]() ;
в)
;
в)
![]() ; г)
; г)
![]() ;
д)
;
д)
![]() ; е)
; е)
![]() .
.
1.0.5. Найти множества точек на комплексной плоскости, удовлетворяющих условиям:
а)
![]() ; б)
; б)
![]() ; в)
; в)
![]() ; г)
; г)
![]() ;
;
д)
![]() ; е)
; е)
![]() ;
;
ж)
![]() ; з)
; з)
![]() ;
;
и)
![]() .
.
1.0.6. Найти действительную и мнимую части указанных функций.
а)
![]() ; б)
; б)
![]() ; в)
; в)
![]() ; г)
; г)
![]() ;
;
1.0.7.
Вычислить: а)
![]() ; б)
; б)
![]() ; в)
; в)
![]() ; г)
; г)
![]() .
.
1.0.8.
Докажите, что если
![]() корень многочлена с действительными
коэффициентами, то
корень многочлена с действительными
коэффициентами, то
![]() также корень.
также корень.
1.0.9.
Докажите основные тригонометрические
соотношения:![]() ,
,
![]() ,
,![]() .
.
Убедиться, что
неравенства
![]() ≤1,
≤1,
![]() ≤1
не выполняются в случае, когда аргумент
тригонометрической функции комплексное
число.
≤1
не выполняются в случае, когда аргумент
тригонометрической функции комплексное
число.
1.0.10. Проверьте справедливость равенств:
a)
![]() ;
b)
;
b)
![]() ;
c)
;
c)![]() ;
d)
;
d)
![]() .
.
1.0.11.
Докажите формулу
Муавра:
![]() .
.
Указание. Использовать тригонометрическую и показательную формы записи.
1.0.12. С
помощью формулы Муавра докажите
равенства:
![]() ,
,
![]() .
.
Указание.
Преобразовать левую часть равенства
![]() ,
затем использовать условие равенства
двух комплексных чисел и тригонометрическое
тождество
.
Проверить справедливость утверждений:
а)
,
затем использовать условие равенства
двух комплексных чисел и тригонометрическое
тождество
.
Проверить справедливость утверждений:
а)
![]() z/n=0;
z/n=0;
б) arg[(-1)n/n] не существует
Ответы
1.0.1.
а)
![]() ;
б)
;
б)![]() ;
;
![]() ;
;
в)![]() г)
г)![]()
1.0.2.
а)![]() б)
б)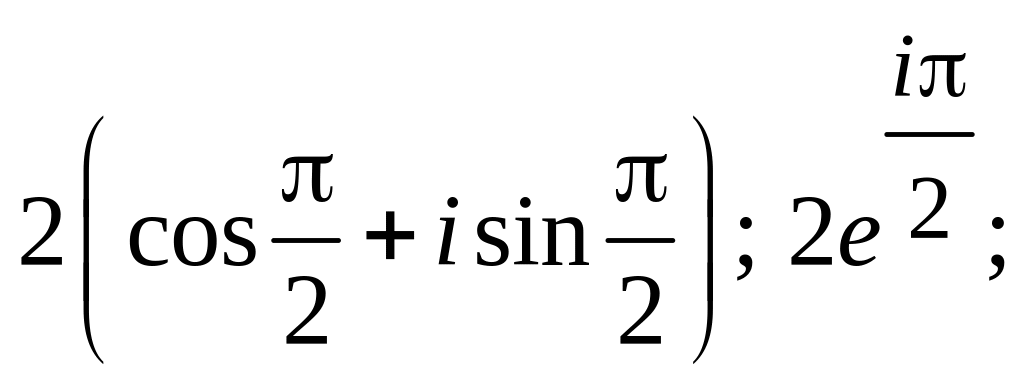
в) г)
г)
д)
е) .
.
1.0.3.
а)![]() б)
б)![]() ; в)
; в)![]() ; г)1728; д)
; г)1728; д)
![]()
1.0.4.
а)![]() б)
б)![]() ,
,
![]() ;
;
в) г)
г)![]() ,
,
![]() ;
;
д)![]() е)
е)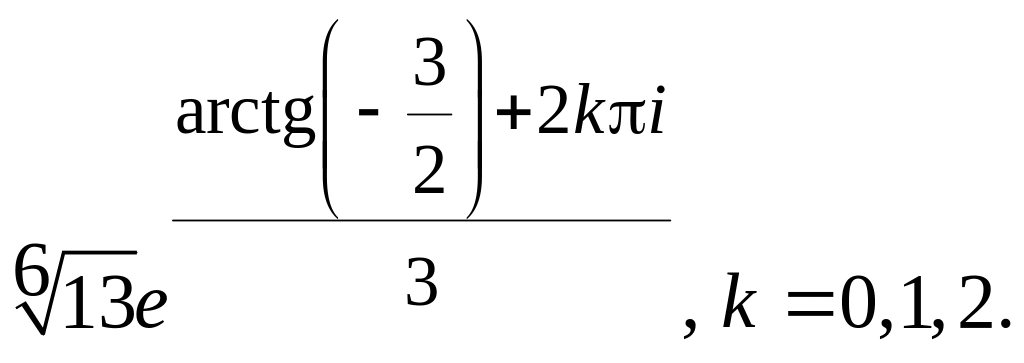
1.0.5.
а)![]() ;
б)
;
б)![]() ;
в)
;
в)![]() ;
г)
;
г)![]() ;
д)
;
д)![]() ;
е)
;
е)![]() ;
ж)
;
ж)![]() ;
з)
;
з)![]() ; и)
; и)![]() .
.
1.0.6.
а)![]() б)
б)![]()
в)
![]() г)
г)![]()
1.0.7. а)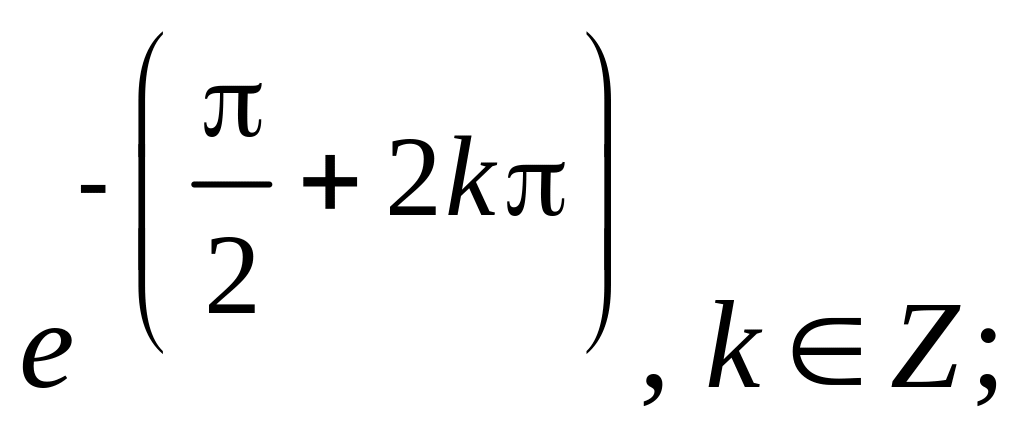 б)
б)![]() в)
в)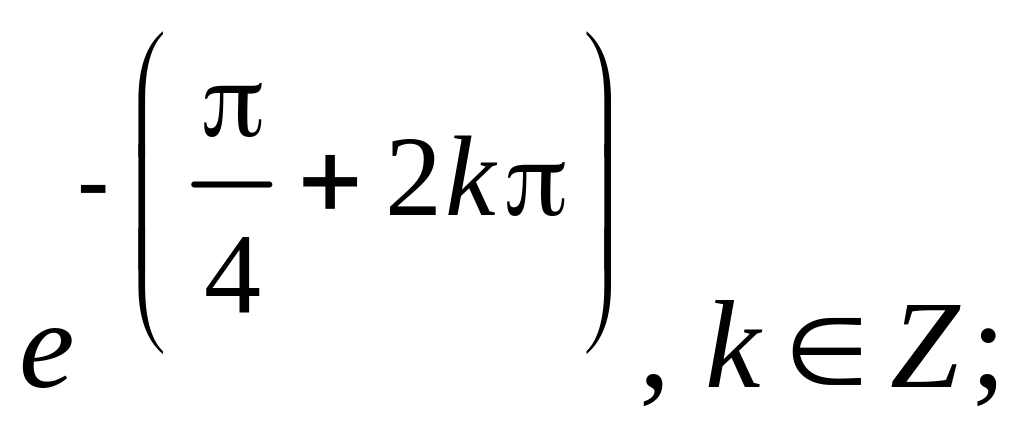 г)
г)![]() .
.
