Теорема разложения:
1.
,
где
(
)
все
особые точки функции
.
Если функция F(p) разлагается в ряд по отрицательным степеням p и, кроме того
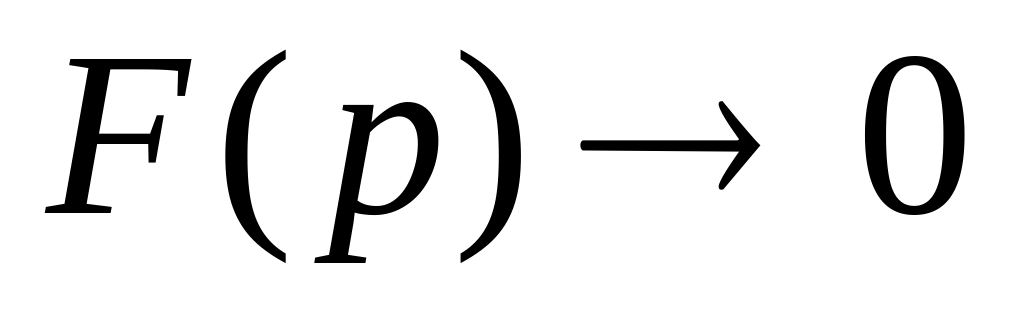при
,
то эта функция
является изображением и может быть
представлена в виде
.
Оригиналом для F(p) служит функция f(t), определяемая при t > 0, сходящимся рядом
.
12)Дифференцирование
и интегрирование по параметру:
Если
и функции
и
,
рассматриваемые как функции переменной
являются оригиналами, то
и
.
Пример 5.1.4. Найти
изображение функции
.
Решение. Используя
свойства линейности, дифференцирования
изображения, а также известные изображения
и
находим
.
Пример
5.1.5. Найти изображение функции
.
Решение. Используя
свойство дифференцирования
изображения, а также известное изображения
находим:
.
Пример
5.1.6. Найти изображение функции
.
Решение.
Используя свойство интегрирования
изображения, а также известное изображение
находим
.
Пример
5.1.7. Найти изображение функции
.
Решение. Используя свойство интегрирования оригинала и результат предыдущего примера, находим
,
.
Пример 5.1.8. Найти
изображение периодической функции
f(t)
с периодом T,
если известно изображение G(p)
функции
Решение. Пусть
.
Используя свойство периодичности
функции f(t)
и изображение
,
преобразуем изображение F(p):
.
Интеграл
заменой t–kT=u
приводится
к виду
.
После преобразований запишем изображение F(p):
.
Пример 5.1.9. Найти
оригинал, если
.
Решение. Наличие
множителя
указывает, на то, что необходимо
использовать теорему об изображении
функции
,
именно
.
11.0.1. Пользуясь определением, найти изображения следующих функций:
а)
; б)
; в)
;
г)
; д)
.
11.0.2.Используя свойства оригиналов и изображений, найти изображения следующих функций:
е)
; ж)
; з)
;
и)
; к)
; л)
;
м)
; н)
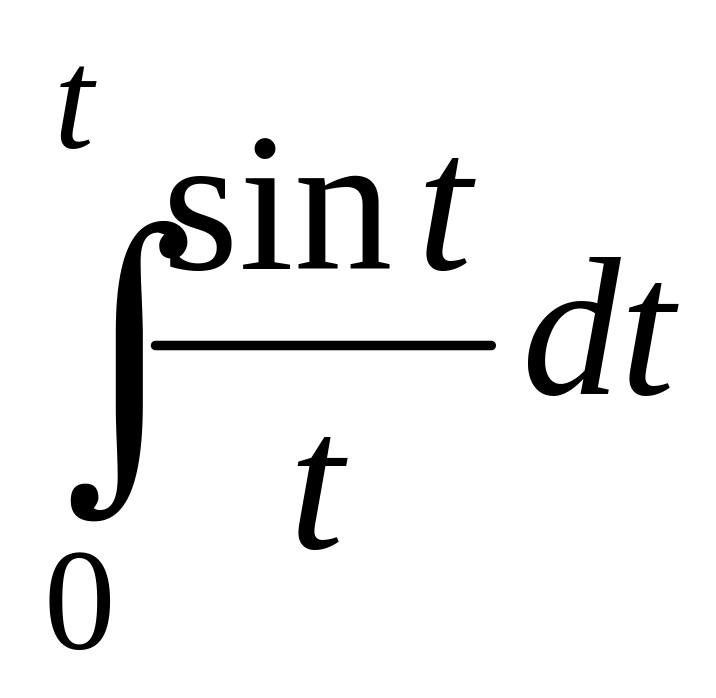; п)
.
11.0.3.Доказать,
что функция
является аналитической функцией при
(рис.5.1.1).
Указание.
Показать, что существует
при
для любого
.
при
.
Законность
дифференцирования несобственного
интеграла по параметру следует из
абсолютной сходимости продифференцированного
интеграла (подынтегральная функция
кусочно-непрерывная).
11.0.4. Доказать, что при стремлении p к бесконечности стремится к нулю.
Указание. В
неравенстве
предположить, что
неограниченно возрастает.
11.0.5. Доказать, что, если функция F(p) удовлетворяет условиям:
1) F(p)
аналитическая для
;
2
при
;
3) для всех
сходится интеграл
.
Тогда при
функция F(p)
является изображением функции f(t)
и определяется обращением
преобразования Лапласа – интегралом
Меллина
(Теорема существования оригинала).
Указание.
Применить
лемму Жордана: F(p)
имеет конечное число изолированных
особых точек
и равномерно относительно
при
.
Тогда для
при
,
где
– левая половина окружности
(рис.5.1.2), затем теорию вычетов.
Ответы
11.0.1. а)
б)
в)
г)
д)
11.0.2.
е)
ж)
з)
и)
к)
л)
м)
н)
;
п)
.