5. Элементы операционного исчисления

5.1. Понятие оригинала и изображения

Комплекснозначная функция действительной переменной называется оригиналом, если она удовлетворяет трем условиям:

1) при всех , причем принимается, что ;

2) на любом конечном отрезке функция имеет не более конечного числа точек разрыва первого рода;

3) существует числа и такие, что

.

Пусть { }обозначает точную нижнюю грань (инфимум) всех чисел , для которых выполняется неравенство 3). Число называется показателем роста (показателем степени роста) функции .

Замечание. Единичной функцией или функцией Хевисайда называется функция

Пример 5.1.1. Пусть - непрерывная на вещественной оси функция. Пусть для некоторого существует предел . Проверить, является ли функция оригиналом, и оценить ее показатель степени роста.

Решение. Функция удовлетворяет условию 1) оригинала, так как при всех . Условие 2) также выполнено в силу предположения о непрерывности функции . Выберем число . По определению предела найдется число , такое, что

(5.1.1) для всех . Положим . В силу непрерывности функции и замкнутости интервала имеет место . Из (5.1.1) следует, что

или . Обозначим через . Тогда , т.е. выполнено последнее условие оригинала. Таким образом, функция - оригинал и ее показатель степени роста не превышает . 

Пример 5.1.2. Пусть - произвольный многочлен степени . Проверить, является ли функция оригиналом, и найти ее показатель степени роста.

Решение. Функция удовлетворяет условию 1) оригинала, так как при всех . Условие 2) также выполнено в силу непрерывности любого многочлена. Применяя раз правило Лопиталя, убедимся, что существует для всех . Таким образом, функция удовлетворяет всем предположениям примера 5.1.1, из которого следует, что - оригинал и ее показатель степени роста не превышает . В силу произвольности выбора получим равенство для показателя степени роста . 

Если - оригинал, то ее преобразование Лапласа ( - комплексная переменная) определяется формулой

. (5.1.2)

Функция комплексной переменной называется также изображением функции . Обозначение: или .

Пример 5.1.3. Найти изображение функции

Решение. По формуле (5.1.2) находим

.

Приведем изображения наиболее часто встречающихся функций.

; ;

( ); ;

; ;

; .

Основные свойства преобразования Лапласа

Приведем основные свойства преобразования Лапласа в нестрогой формулировке:

1. Линейность: , .

2. Подобие: , .

3. Теорема запаздывания: .

4. Теорема смещения: , .

5. Изображение производной:

, .

6. Изображение интеграла: .

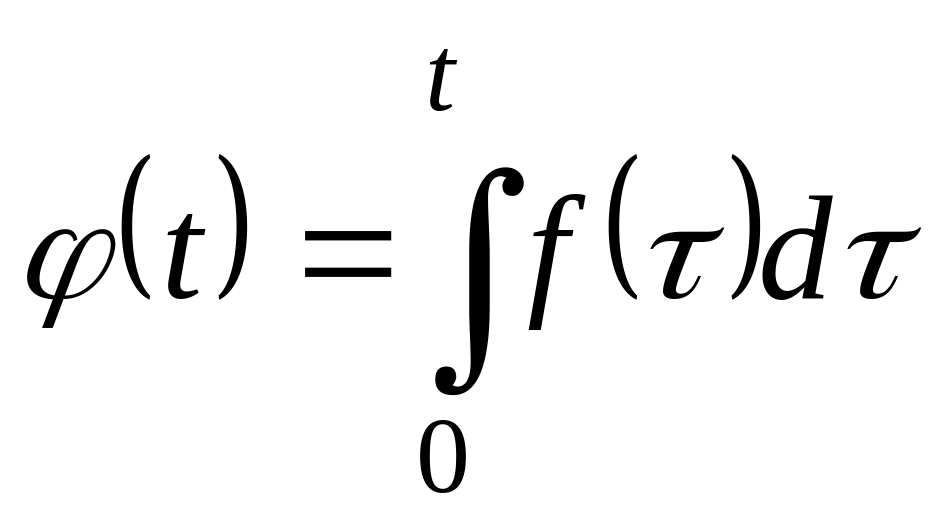
7. Дифференцирование изображения: .

8. Интегрирование изображения: .

9. Изображение свертки (теорема Бореля):

.

10. Интеграл Дюамеля:

.