
- •Содержание
- •1. Основные понятия теории функций комплексной переменной
- •1.1. Комплексные числа. Основные элементарные функции комплексной переменной
- •1. 2. Условия Коши – Римана. Аналитические функции
- •1.3. Интеграл от функции комплексной переменной
- •2. Ряды
- •2.1. Сумма числового ряда. Признаки абсолютной сходимости
- •В случае ряд сходится,
- •В случае ряд расходится и не выполнено необходимое условие сходимости,
- •В случае ничего сказать нельзя.
- •2.2. Условная сходимость
- •2.3. Функциональные ряды
- •3. Особые точки и разложения в ряды
- •3.2. Классификация изолированных особых точек
- •4. Теория вычетов
- •4.1. Вычет
- •4.2. Применение вычетов к вычислению интегралов
- •5. Элементы операционного исчисления
- •5.1. Понятие оригинала и изображения
- •Теорема разложения:
- •5.2. Восстановление оригинала по изображению
- •1. Линейные дифференциальные уравнения
- •2. Системы обыкновенных дифференциальных уравнений
4.2. Применение вычетов к вычислению интегралов
1) Интегралы вида
![]() ,
где
,
где
![]() -символ
рациональной функции, с помощью замены
-символ
рациональной функции, с помощью замены
![]() приводятся к контурным интегралам от
рациональных относительно
функций.
приводятся к контурным интегралам от
рациональных относительно
функций.
Пример 4.2.1.
Вычислить интеграл
![]() с
помощью вычетов.
с
помощью вычетов.
Решение. Выполним замену переменной .
 .
.
Применим первую
теорему о вычетах. Подынтегральная
функция имеет две особые точки
![]() ,
,
![]() - простые полюсы, однако внутри контура
располагается только
.
Поэтому
- простые полюсы, однако внутри контура
располагается только
.
Поэтому
![]() .
Отсюда
.
Отсюда
![]() .
.
Пример 4.2.2.
Вычислить интеграл
![]() с
помощью вычетов.
с
помощью вычетов.
Решение. Выполним замену переменной .
 .
.
Применим первую
теорему о вычетах. Подынтегральная
функция имеет две особые точки
![]() ,
,
![]() -
простые полюсы, однако внутри контура
располагается только
.
Поэтому
-
простые полюсы, однако внутри контура
располагается только
.
Поэтому
![]() .
Отсюда
.
Отсюда
![]() .
.
2) Интегралы вида
![]() .
.
Интегралы вида
,
где
![]() ,
,![]() -
многочлены степени
и
,
соответственно, причем
-
многочлены степени
и
,
соответственно, причем
![]() ,
а
не имеет вещественных корней, вычисляются
по формуле
,
а
не имеет вещественных корней, вычисляются
по формуле
 ,
(4.2.1) где
,
(4.2.1) где
![]() -
все корни
-
все корни
![]() ,
расположенные в верхней полуплоскости.
,
расположенные в верхней полуплоскости.
Пример 4.2.3. Вычислить
![]() .
.
Решение. Находим
корни многочлена
![]() из равенства
из равенства
![]() .
Числа
.
Числа
![]() ,
,
![]() - корни кратности два знаменателя, не
являющиеся корнями числителя. Поэтому
,
- полюсы второго порядка функции
- корни кратности два знаменателя, не
являющиеся корнями числителя. Поэтому
,
- полюсы второго порядка функции
![]() .
Отбрасываем полюс
,
поскольку расположен в нижней
полуплоскости.
.
Отбрасываем полюс
,
поскольку расположен в нижней
полуплоскости.
По формуле (4.2.1) вычисляем
 .
Заметим, что
.
Заметим, что
![]() .
Отсюда
.
Отсюда
![]()
Пример 4.2.4.
Вычислить
![]() .
.
Решение. Заметим,
что подынтегральная функция четная.
Поэтому справедливо равенство![]() .Используя
результат предыдущего примера, получим
.Используя
результат предыдущего примера, получим![]() .
.
3) Интегралы вида
![]() ,
,![]() ,
,![]()
Интегралы вида
,
,
где
![]() ,
,
-
многочлены степени
и
,
соответственно, причем
,
,
-
многочлены степени
и
,
соответственно, причем
![]() ,
а
не имеет вещественных корней, вычисляются
по формулам:
,
а
не имеет вещественных корней, вычисляются
по формулам:
 ,
(4.2.2)
,
(4.2.2)
![]() ,
(4.2.3)
,
(4.2.3)
![]() ,
где
-
все корни
,
расположенные в верхней полуплоскости.
,
где
-
все корни
,
расположенные в верхней полуплоскости.
Пример 4.2.5.
Вычислить
![]() .
.
Решение. Находим
корни многочлена
![]() из равенства
из равенства
![]() .
Числа
.
Числа
![]() ,
,
![]() - корни кратности два знаменателя, не
являющиеся корнями числителя. Поэтому
,
- полюсы второго порядка функции
- корни кратности два знаменателя, не
являющиеся корнями числителя. Поэтому
,
- полюсы второго порядка функции
![]() .
Отбрасываем полюс
,
поскольку расположен в нижней
полуплоскости.
.
Отбрасываем полюс
,
поскольку расположен в нижней
полуплоскости.
По формуле (4.2.2) вычисляем

Заметим, что
![]() .
.
Отсюда
![]() .
.
Пример 4.2.6.
Вычислить
![]() .
.
Решение. Заметим, что подынтегральная функция четная. Поэтому справедливо равенство
![]() .
.
По формуле (4.2.3)
![]() .
.
Используя результат предыдущего примера, получим
![]() .
.
10.0.1.С помощью вычетов вычислить интегралы
а)
 ; б)
; б)
 ; в)
; в)
 ;
;
г)
; д)
 ; е)
; е)
![]() ;
;
ж)
 ; к)
; к)
![]() ; л)
; л)
 ;
;
м)
 ; н)
; н)
 ; о)
; о)
![]() .
.
10.0.2.Вычислить интегралы
а)
 ; б)
; б)
 ; в)
; в)
![]() ;
;
г)
 ; д)
; д)
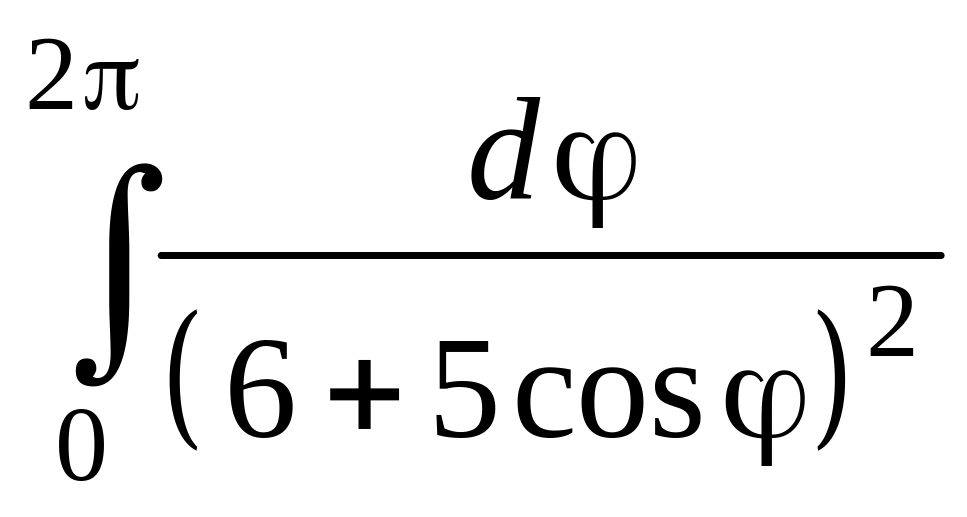 ; е)
; е) ;
;
ж) ; к)
; к)
 ; л)
; л)
 ;
;
м)
 ;
н)
;
н)
 ;
о)
;
о)
 ;
;
п)
 ; р)
; р)
 .
.
Ответы
10.0.1. а)
![]() ; б)
; б)
![]() ; в)
; в)
![]() ;
;
г)
; д)
е)![]() ж)
ж)
к) 0 ; л) 0 ;
м)
н)![]() о)
о)
![]() .
.
10.0.2. а)![]() ; б)
; б)![]() в)
в)
![]() ; г)
; г)![]()
д) ![]() е)
ж)
е)
ж)![]() к)
л)
к)
л)![]()
м)![]() н)
н)![]() о)
о)![]()
п)![]() р)
р)![]()
