4. Теория вычетов

4.1. Вычет

Пусть - изолированная особая точка функции . Комплексное число , где - замкнутый контур, который можно стянуть к , оставаясь в кольце аналитичности функции , называется вычетом в точке .

Очевидно, в разложении (3.1.1).

Формулы вычисления вычетов:

1. - устранимая особая точка .

2. - полюс 1-го порядка (простой полюс)

.

Если , , , , то

.

3. - полюс порядка

.

4. - существенно особая точка 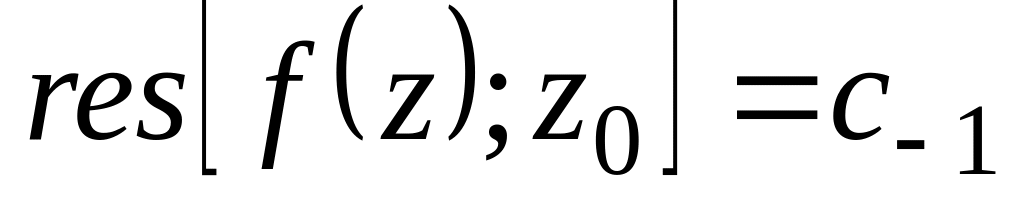(нахождению вычета предшествует разложение в ряд Лорана (3.1.1)).

Пример 4.1.1. Для функции найти вычеты во всех изолированных особых точках.

Решение. Используя результат примера 3.2.3, а именно: ( ) - полюсы второго порядка, - простой полюс, точка не является изолированной особой точкой. По формуле для простого полюса по первому замечательному пределу находим

.

Для полюсов второго порядка

.

Заметим, что

.

Отсюда

.

Для точки вычет не находится, так как она не является изолированной особой точкой.

Первая теорема о вычетах

Пусть - аналитическая функция в области , за исключением конечного числа изолированных особых точек , , …, , лежащих в этой области. Тогда для любого простого замкнутого контура , охватывающего точки , , …, ,

.

Пример 4.1.2. Вычислить .

Решение. Особые точки подынтегральной функции для всех целых . Заметим, что внутрь контура попадают точки , . Используя результат примера 4.1.1, а именно: и первую теорему о вычетах, находим

.

Вычет в бесконечно удаленной точке. Вторая теорема о вычетах

Пусть - изолированная особая точка функции .

Вычетом функции в бесконечно удаленной точке называется комплексное число

где – произвольный замкнутый контур, вне которого не имеет особых точек, за исключением .

Замечание. Если - устранимая особая точка, то вычет в ней может быть отличен от .

Вторая теорема о вычетах. Пусть аналитична на всей комплексной плоскости, за исключением изолированных особых точек , , …, и . Тогда .

9.0.1.Найти вычеты в конечных особых точках следующих функций.

а) ; б) ; в) ; г) ; д) ; е) ; ж) ; к) ; л) .

Ответы

9.0.1. а) при , 0; при , ; б) в) при при г) 0 ; д) при при , ; е) ж) при при к) 0 ; л)