2. Силовой расчет исходного механизма

Изображаем звено в масштабе μ_l=0,004м/мм , прикладывая в точку А

известную реакцию (которая равна и противоположна по направлению ). Освобождаем звено от связей со стойкой и прикладываем вместо нее реакцию . На кривошип действует сила тяжести в точке S₁ (рис 3.3).

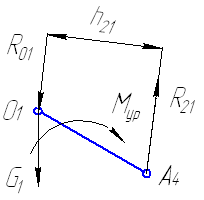
Рис. 3.3 Схема нагружения исходного механизма

Уравновешивающий момент М_ур определим из уравнения равновесия кривошипа в форме моментов относительно точки О_1.

,

где:

,

м.

Н*м.

Для нахождения неизвестной реакции построим план сил для данной схемы.

План сил действующих на кривошип и таблица со значениями сил приведены на рис. 3.4.

Рис. 3.4. План сил кривошипа

2. Силовой расчет методом «жесткого рычага» н.Е. Жуковского

Для проверки правильности построения планов сил и определения реакций в кинематических парах механизма необходимо определить уравновешивающую силу на входном звене с помощью теоремы Н.Е.Жуковского о «жестком рычаге» Из полюса Р, в произвольном масштабе переносим план скоростей, повернутый на против часовой стрелки, относительно его нормального положения. В концы векторов скоростей точек, в которых действуют приложенные к механизму силы, переносим их, сохраняя направление, а именно: - сила полезного сопротивления приложенная к выходному звену; , - сила инерции звеньев 2, 3;

, ,- силы тяжести, действующие на соответствующие звенья. Уравновешивающая сила действует перпендикулярно кривошипу моменты сил инерции рассчитываем по формулам[1,2]:

(направления момента на плане сил и на схеме для расчета по теореме Жуковского совпадают так как точки а и b занимают такое же положение как и точки А и В на разметке механизма);

,

где - длинa звена AB , м;

Составляем уравнение равновесия плана скоростей как условного жесткого рычага в форме моментов сил относительно полюса плана скоростей:

Решая это уравнение относительно , получаем

Выразим :

;

Определяем :

Проверим погрешность измерений сделанных двумя способами нахождения уравновешивающего момента (метод планов и метод «жесткого рычага» Н.Е. Жуковского:

Момент уравновешивающий[1,2]: .

Н*м.

Определим погрешность:

,

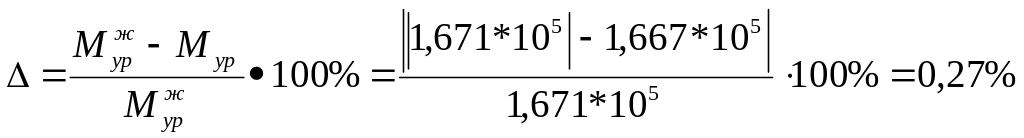
Схема «жесткого рычага» Н.Е. Жуковского показана на рис. 3.5.

рис. 3.5 Схема Рычага Жуковского

Расчет других положений производится аналогично приведенному выше расчету.

Для положения №5 имеем:

Заключение

При решении первого раздела был выполнен структурный анализ механизма подачи, а именно: была рассчитана подвижность механизма, было рассмотрена структура механизма.

Во втором разделе «Кинематический анализ» были произведены расчеты по определению перемещений, ускорений, скоростей выходного звена механизма методом планов и методом кинематических диаграмм.

В заключительном третьем разделе рассмотрены построение планов сил действующих на звенья, реакции в кинематических парах; уравновешивающая сила определена методом плана сил и методом рычага Н.Е. Жуковского. Результаты можно считать достоверными т.к. относительная погрешность значения уравновешивающего момента входит в пределы 10% а именно составляет 0,27% ( для механизма в 4-ом положении рабочего хода), 0,3% для 5-го положения

БИБЛИОГРАФИЧЕСКИЙ СПИСОК

1. Артоболевский И. И. Теория механизмов и машин. Учебник для вузов - М.: Наука, 1988, 640 с.

2. Кинетостатика плоских механизмов и динамика машин. Учебное пособие. Составители: Н.Н. Федоров., Издательство ОмГТУ, Омск 2000, 144 с.

3. Проектирование и кинематика плоских механизмов. Учебное пособие. Составители: Н.Н. Федоров., Издательство ОмГТУ, Омск 2000, 144 с.