2. Постановка и решение детерминированной задачи линейного программирования

Решение задач математического программирования состоит из этапов:

• математической постановки задачи;

• постановки задачи на рабочем листе Excel;

• задание условий решения задачи в диалоговом окне «Поиск решения»;

• задание параметров решения задачи в окне «Параметры поиска решения»

• выполнения задачи;

• анализ результатов решения задачи и создание отчетов по результатам решения задачи.

Формулировка задачи. Требуется определить, в каком количестве надо выпускать продукцию 4-х типов, чтобы получить максимально возможный валовой доход. Для изготовления продукции требуются ресурсы трех видов: трудовые, сырье, финансы. В таблице 3.1 приведены нормы расходов ресурсов на единицу каждого вида продукции, а также запасы ресурсов. В таблице 3.2 приведены рыночные цены на единицу продукции [6,7].

Таблица 3.1 – Исходные по запасам и нормам затрат ресурсов на производство (внутренние данные)

Ресурс	Продукция					Запас ресурса
	1	2	3	4
Трудовые	1	1	1	1	16
Сырье	6	5	4	3	110
Финансы	4	6	10	13	100

Таблица 3.2 – Внешние данные о ценах на продукцию предприятия

Рыночная цена единицы продукция
1	2	3	4
60	70	120	130

Решение задачи начинают с выявления класса задач и ее математической постановки.

Сформулированная выше задача может быть сформулирована в терминах задач математического программирования и решена методами, предлагаемыми этим разделом математики. Сначала необходимо сформулировать функцию цели. В качестве функции цели здесь выступает валовой доход, который нужно максимизировать. Сама функция цели зависит от 4 переменных, которые представляют собой объемы выпуска продукции, которые ее максимизируют.

Введем обозначения. Пусть Х₁, Х₂, Х₃ и Х₄ – это объемы выпускаемой продукции, тогда

f (Х₁, Х₂, Х₃, Х₄) = 60 Х₁ + 70 Х₂ + 120 Х₃ + 130 Х₄ MAX (3.1)

При этом должны быть соблюдены нормы затрат ресурсов в рамках их запасов, что можно выразить системой неравенств:

Х₁ + Х₂ + Х₃ + Х₄  16

6Х₁ + 5Х₂ + 4Х₃ + 3Х₄  110 (3.2)

4Х₁ + 6Х₂ + 10Х₃ + 13Х₄  100

Х_i  0 , I = 14

Анализ созданной математической модели показывает, что задача в данной постановке относится к задачам линейного программирования, т.к. функция цели и ограничения представляют собой линейные выражения.

Для решения данного типа задач в EXCEL предусмотрена процедура ПОИСК РЕШЕНИЯ, которая находится в меню СЕРВИС. Перед тем как воспользоваться этой процедурой необходимо подготовить рабочий лист, на котором будет выполнена математическая постановка задачи (см. рис. 3.1 и рис. 3.2). В строке 2 в ячейках В2:Е2 приведены начальные значения переменных Х₁, Х₂, Х₃ и Х₄. эти ячейки носят название Изменяемые ячейки, в них будет находиться оптимальный план решения задачи или те значения переменных, при которых функция цели достигает своего оптимального значения. Нижняя и верхняя граница предусмотрена для возможных значений минимальной и максимальной емкости рынка по каждому продукту, коэффициенты – это рыночные цены единицы каждого продукта, заданные как исходные данные в таблице 3.2. В ячейке F5 задна формула для вычисления функции цели. В ячейках В8:Е10 приведены нормы затрат ресурсов на производство единицы продукции каждого вида, которые заданы в таблице 3.1. В ячейках F8:Н10 заданы линейные ограничения в виде значения левой части неравенства (затраты ресурса) м правой части неравенства (запасы ресурса).

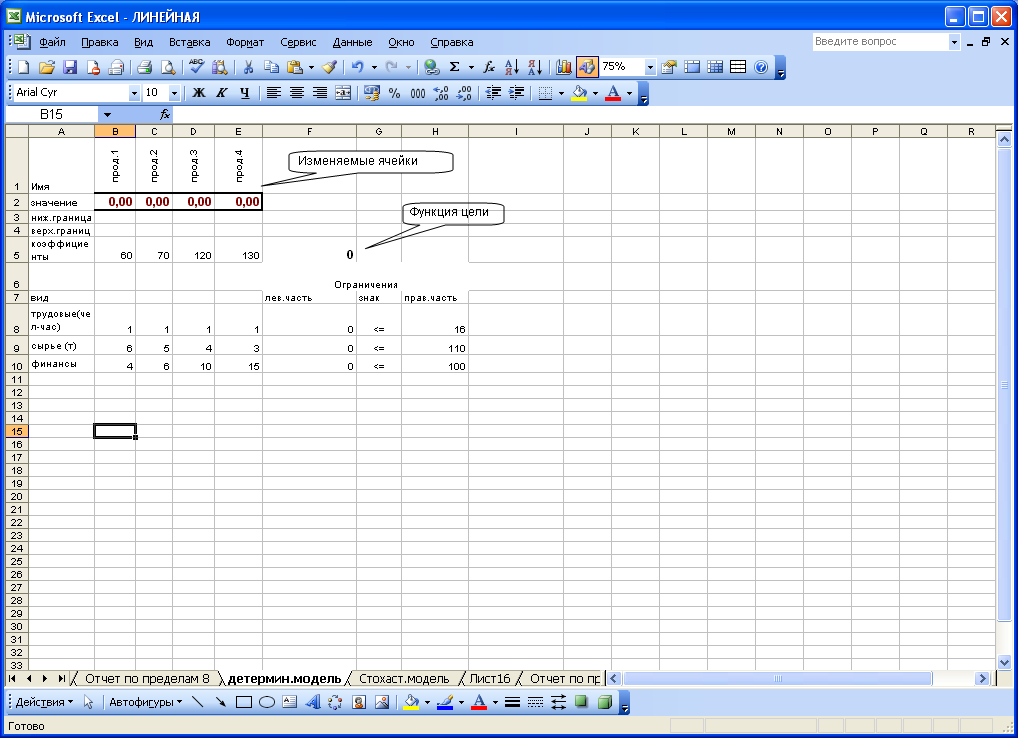
Рис. 3.1 – Пример размещения математической постановки задачи на рабочем листе

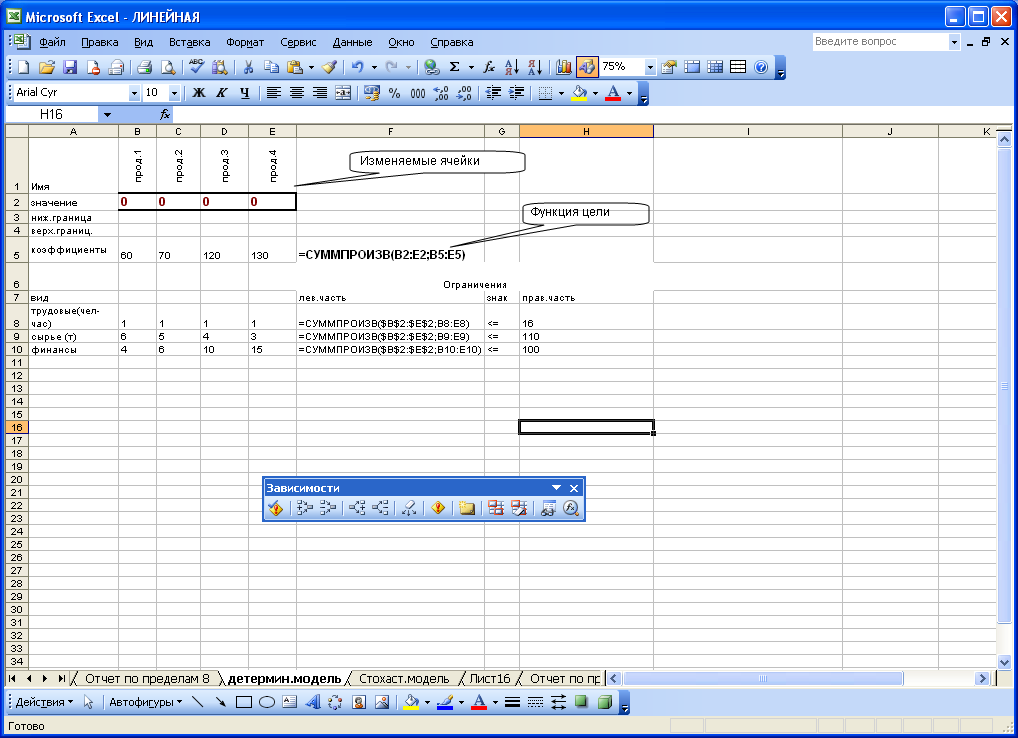
Рис. 3.2 – Математическая постановка задачи на рабочем листе

После этого можно приступать к решению задачи с использованием процедуры ПОИСК РЕШЕНИЯ. Если процедура ПОИСК РЕШЕНИЯ отсутствует в меню СЕРВИС, ее нужно надстроить. После вызова процедуры появляется диалоговое окно (рис. 3.3), которое нужно соответствующим образом заполнить (см. Элементы диалогового окна «ПОИСК РЕШЕНИЯ».

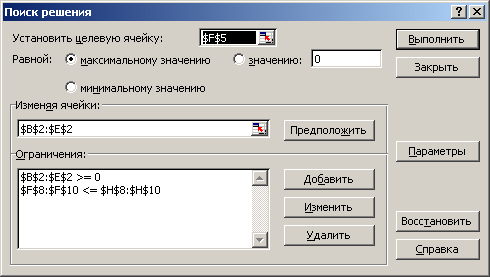
Рис. 3.3 – Диалоговое окно процедуры Поиск решения

3.2.1 Элементы диалогового окна «Поиск решения»

Для решения задачи необходимо заполнить поля диалогового окна процедуры «Поиск решения»

Установить целевую ячейку

Служит для указания целевой ячейки, значение которой необходимо максимизировать, минимизировать или установить равным заданному числу. Эта ячейка должна содержать формулу.

Равно

Служит для выбора варианта оптимизации значения целевой ячейки (максимизация, минимизация или подбор заданного числа). Чтобы установить число, введите его в поле.

Изменяя ячейки

Служит для указания ячеек, значения которых изменяются в процессе поиска решения до тех пор, пока не будут выполнены наложенные ограничения и условие оптимизации значения ячейки, указанной в поле Установить целевую ячейку.

Предположить

Используется для автоматического поиска ячеек, влияющих на формулу, ссылка на которую дана в поле Установить целевую ячейку. Результат поиска отображается в поле Изменяя ячейки.

Ограничения

Служит для отображения списка граничных условий поставленной задачи.

Добавить

Служит для отображения диалогового окна Добавить ограничение (рис.3.4).

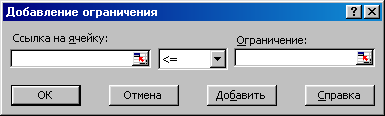
Рис. 3.4 – Добавление ограничений

Изменить

Служит для отображения диалоговое окна Изменить ограничение.

Удалить

Служит для снятия указанного ограничения.

Выполнить

Служит для запуска поиска решения поставленной задачи.

Закрыть

Служит для выхода из окна диалога без запуска поиска решения поставленной задачи. При этом сохраняются установки сделанные в окнах диалога, появлявшихся после нажатий на кнопки Параметры, Добавить, Изменить или Удалить.

Параметры

Служит для отображения диалогового окна Параметры поиска решения, в котором можно загрузить или сохранить оптимизируемую модель и указать предусмотренные варианты поиска решения (см. рис. 3.5). Если модель линейная, то нужно установить флажок Линейная модель. Это существенно влияет на способ решения задачи (Симплекс-метод используется для решения задач линейного программирования и метод множителей Лагранжа – для задач нелинейного программирования). См. ниже вставку Элементы диалогового окна «Параметры поиска решения».

Восстановить

Служит для очистки полей окна диалога и восстановления значений параметров поиска решения, используемых по умолчанию

Рис. 3.5 – Параметры задачи

3.2.2 Элементы диалогового окна «Параметры поиска решения»

Можно изменять условия и варианты поиска решения для линейных и нелинейных задач, а также загружать и сохранять оптимизируемые модели. Значения и состояния элементов управления, используемые по умолчанию, подходят для решения большинства задач.

Максимальное время

Служит для ограничения времени, отпускаемого на поиск решения задачи. В поле можно ввести время (в секундах) не превышающее 32767; значение 100, используемое по умолчанию, подходит для решения большинства простых задач.

Число итераций

Служит для управления временем решения задачи, путем ограничения числа промежуточных вычислений. В поле можно ввести время (в секундах) не превышающее 32767; значение 100, используемое по умолчанию, подходит для решения большинства простых задач.

Точность

Служит для задания точности, с которой определяется соответствие ячейки целевому значению или приближение к указанным границам. Поле должно содержать десятичную дробь от 0 (нуля) до 1. Чем больше десятичных знаков в задаваемом числе, тем выше точность — например, число 0,0001 представлено с более высокой точностью, чем 0,01.

Допустимое отклонение

Служит для задания допуска на отклонение от оптимального решения, если множество значений влияющей ячейки ограничено множеством целых чисел. При указании большего допуска поиск решения заканчивается быстрее.

Сходимость

Когда относительное изменение значения в целевой ячейке за последние пять итераций становится меньше числа, указанного в поле Сходимость, поиск прекращается. Сходимость применяется только к нелинейным задачам, условием служит дробь из интервала от 0 (нуля) до 1. Лучшую сходимость характеризует большее количество десятичных знаков — например, 0,0001 соответствует меньшему относительному изменению по сравнению с 0,01. Лучшая сходимость требует больше времени на поиск оптимального решения.

Линейная модель

Служит для ускорения поиска решения линейной задачи оптимизации.

Показывать результаты итераций

Служит для приостановки поиска решения для просмотра результатов отдельных итераций.

Автоматическое масштабирование

Служит для включения автоматической нормализации входных и выходных значений, качественно различающихся по величине — например, максимизация прибыли в процентах по отношению к вложениям, исчисляемым в миллионах рублей.

Значения не отрицательны

Позволяет установить нулевую нижнюю границу для тех влияющих ячеек, для которых она не была указана в поле Ограничение диалогового окна Добавить ограничение.

Оценка

Служит для указания метода экстраполяции — линейная или квадратичная — используемого для получения исходных оценок значений переменных в каждом одномерном поиске.

Линейная.    Служит для использования линейной экстраполяции вдоль касательного вектора.

Квадратичная.    Служит для использования квадратичной экстраполяции, которая дает лучшие результаты при решении нелинейных задач.

Производные

Служит для указания метода численного дифференцирования — прямые или центральные производные — который используется для вычисления частных производных целевых и ограничивающих функций.

Прямые.    Используется в большинстве задач, где скорость изменения ограничений относительно невысока.

Центральные.    Используется для функций, имеющих разрывную производную. Данный способ требует больше вычислений, однако его применение может быть оправданным, если выдается сообщение о том, что получить более точное решение не удается.

Метод

Служит для выбора алгоритма оптимизации — метод Ньютона или сопряженных градиентов — для указания направление поиска.

Метод Ньютона.    Реализация квазиньютоновского метода, в котором запрашивается больше памяти, но выполняется меньше итераций, чем в методе сопряженных градиентов.

Метод сопряженных градиентов.    Реализация метода сопряженных градиентов, в котором запрашивается меньше памяти, но выполняется больше итераций, чем в методе Ньютона. Данный метод следует использовать, если задача достаточно велика и необходимо экономить память, а также если итерации дают слишком малое отличие в последовательных приближениях.