4.3 Частотные критерии устойчивости

В уравнении (4.2) заменим на , получим характеристический вектор:

(4.7)

Если корень характеристического уравнения расположен слева от мнимой оси, то вектор поворачивается на угол , если этот корень находится на комплексной плоскости справа от мнимой оси, то вектор поворачивается на угол .

Определим изменение аргумента вектора при изменении частоты :

.

Пусть корней характеристического уравнения расположены справа от мнимой оси, а остальные корней – слева.

Тогда .

В устойчивой системе , тогда

(4.8)

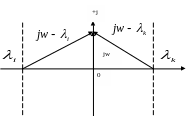
Рис.4.1. К оценке изменения аргумента характеристического вектора

Из выражения (4.8) следует критерий устойчивости Михайлова:

,

где и V - действительная и мнимая части характеристического вектора.

Критерий Михайлова. Система радиоавтоматики устойчива, если годограф характеристического вектора (изображение частотной характеристики на плоскости частотного переменного), начинаясь на положительной части действительной оси, обходит последовательно в положительном направлении квадрантов, где - порядок характеристического уровня системы.

Если годограф проходит через начало координат, то система находится на границе устойчивости. В этом случае

.

Из этих уравнений можно определить значения параметров, при которых система находится на границе устойчивости.

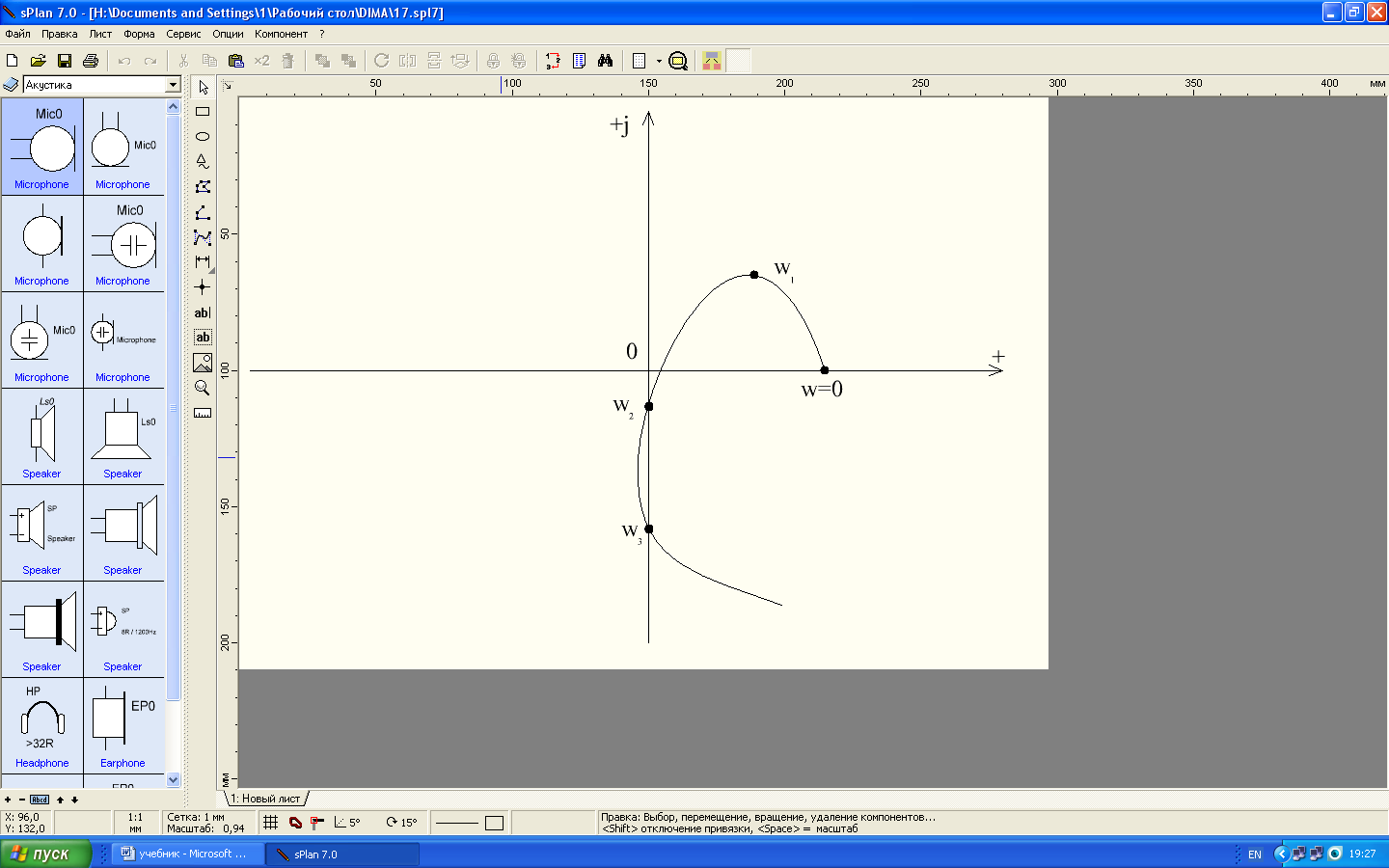
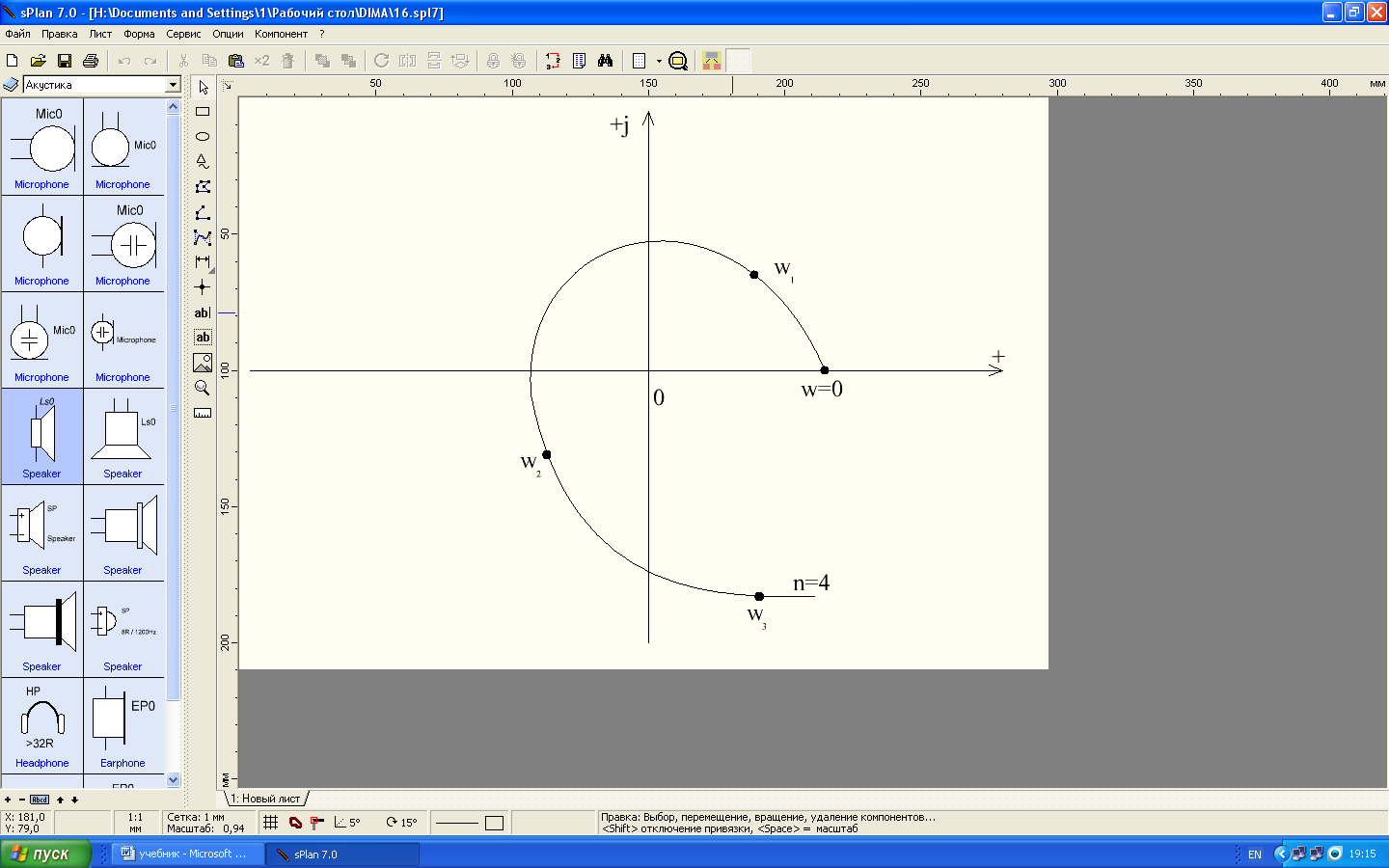
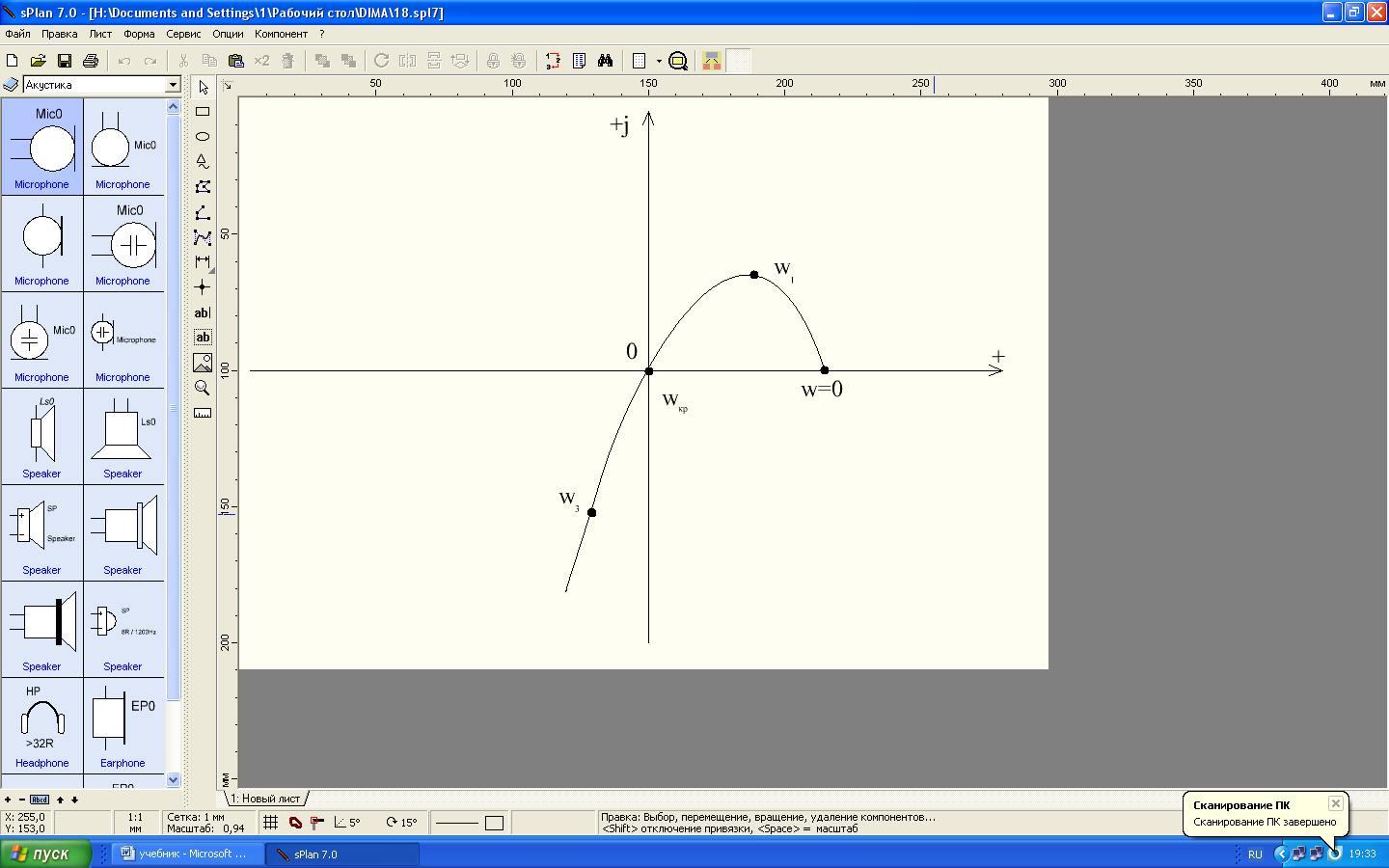
a) б) в)

Рис. 4.2. Общий вид характеристического вектора:

а – устойчивой системы; б- неустойчивой системы; в- системы на границе устойчивости.

Критерий Найквиста. Система радиоавтоматики, устойчивая в разомкнутом состоянии, будет устойчива и в замкнутом состоянии, если годограф частотной характеристики разомкнутой системы не охватывает точку с координатами . В том случае, когда годограф частотной характеристики охватывает эту точку, система неустойчива.

Введём вектор ,

где

- частотная характеристика разомкнутой системы,

- характеристический вектор замкнутой системы,

- характеристический вектор разомкнутой системы.

Определим изменение аргумента вектора для случая, когда замкнутая система устойчива:

Изменение аргумента вектора будет равно нулю, если годограф частотной характеристики разомкнутой системы не охватывает точку с координатами .

4.4 Запасы устойчивости

При проектировании следует обеспечить определённые запасы устойчивости системы, которые характеризуют близость годографа частотной характеристики разомкнутой системы к точке с координатами . Запасы устойчивости определяются на двух частотах: частоте среза, при которой амплитудно-частотная характеристика разомкнутой системы равна единице и критической частоте, при которой фазочастотная характеристика равна .

Различают запас устойчивости по фазе и усилению. Запас устойчивости по фазе показывает, на какое значение фазочастотная характеристика разомкнутой системы на частоте среза отличается от :

Запас устойчивости по усилению определяет, во сколько раз нужно увеличить коэффициент усиления, чтобы система оказалась на границе устойчивости. Запас устойчивости по усилению вычисляется по формуле:

.

Cистемы радиоавтоматики, годографы частотных характеристик которых пересекают вещественную ось только справа от точки с координатами называют абсолютно устойчивыми.

Если годограф частотной характеристики разомкнутой системы пересекает вещественную ось и слева от точки с координатами , то систему называют условно устойчивой. Неустойчивой такая система может быть как при увеличении, так и при уменьшении коэффициента усиления. Для нормальной работы системы радиоавтоматики необходимо, чтобы запас устойчивости по усилению был , а запас устойчивости по фазе .