4.1.1. Необходимое условие устойчивости
В соответствии с необходимым условием устойчивости все коэффициенты характеристического уравнения (4.1) должны быть больше нуля.
Представим (4.1) в виде:
.
(4.4)
Если система устойчива, т.е. все корни отрицательные, то, раскрыв скобки в (4.4) получим уравнение с положительными коэффициентами. Если система неустойчива, т.е. хотя бы один из корней положительный, то перемножив сомножители в (4.4), получим уравнение с несколькими отрицательными коэффициентами.
4.2 Критерий устойчивости Гурвица
Для оценки устойчивости системы радиоавтоматики по критерию Гурвица необходимо из коэффициентов характеристического уравнения (4.1) составить матрицу Гурвица. Перепишем (4.1) в виде:
Матрица Гурвица имеет вид:
(4.5)
Порядок составления
матрицы Гурвица следующий. В левом
верхнем углу матрицы записывается
коэффициент
,
по главной диагонали располагаются
коэффициенты характеристического
уравнения с младшими индексами, над
элементами главной диагонали записываются
коэффициенты с убывающими индексами,
под элементами – с возрастающими.
Для оценки устойчивости системы радиоавтоматики необходимо вычислить определители Гурвица, которые получают из матрицы (4.5) путём вычёркивания равного числа строк и столбцов в левом верхнем углу матрицы. Например, первый определитель имеет вид:
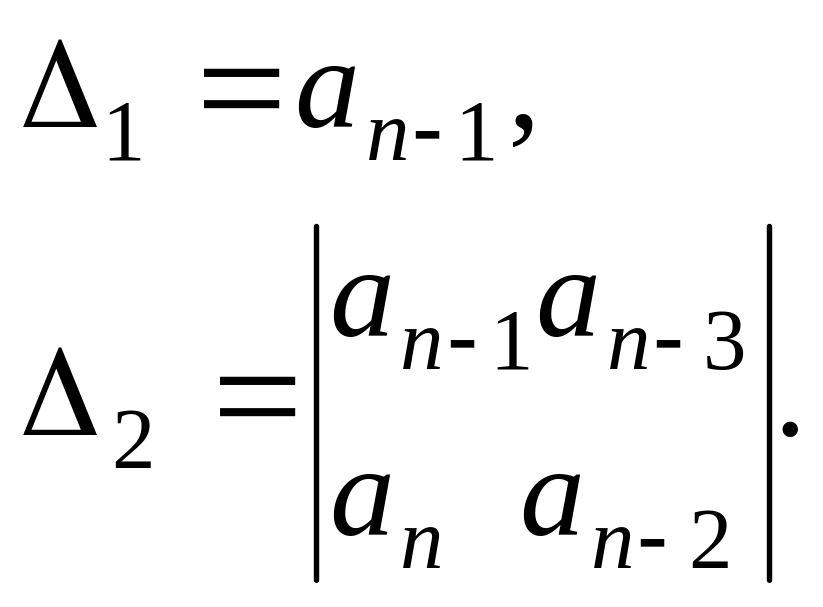
Система радиоавтоматики
устойчива, если при
(4.6)
Раскрыв
по последнему столбцу, получим:
Так как
,
то для проверки устойчивости системы
достаточно уточнить знаки только до
определителя. Если
,
то система радиоавтоматики находится
на границе устойчивости. Возможны два
случая:
1) cвободный член характеристического уравнения равен нулю, что соответствует нейтрально устойчивой системе;
2)
,
что соответствует колебательной границе
устойчивости.
Из условия
вычисляется критический коэффициент
усиления
,
соответствующий границе устойчивости.
Отношение
называют
запасом устойчивости по усилению, где
-
коэффициент передачи. Для нормального
функционирования системы необходимо,
чтобы
Пример
4.1. Оценить устойчивость системы,
cостоящей
из двух последовательно соединённых
звеньев с передаточными функциями
и
.
Так как звенья соединены последовательно, то передаточная функция разомкнутой системы имеет вид:
Так как характеристическое уравнение имеет вид:
,
то
,
.
Так как это выражение
равно нулю, если равен нулю числитель,
то рассмотрим уравнение
.
Выпишем коэффициенты:
Cоставим
матрицу Гурвица:
.
Так как
,
,
,
то по критерию Гурвица система устойчива.
Пример
4.2. Для системы, передаточная функция
которой в разомкнутом состоянии
определить запас устойчивости по
усилению.
Запас устойчивости по усилению рассчитывается по формуле:
,
где
-
коэффициент усиления. Критический
коэффициент усиления находится из
условия
после составления матрицы Гурвица:
,
cледовательно
.
После преобразований получаем уравнение:
Раскрыв скобки, приходим к уравнению:
Выпишем коэффициенты:
,
,
,
.
Cоставим
матрицу Гурвица:
.
Рассмотрим минор
.
Критический коэффициент усиления ищется
из условия:
.
Тогда
Следовательно,
запас устойчивости по усилению
рассчитывается следующим образом:
