8.2 Метод фазовой плоскости

В ряде случаев поведение следящей системы описывается нелинейным дифференциальным уравнением 2-го порядка:

(8.1)

Обозначив , уравнение (8.1) можно заменить системой уравнений 1-го порядка:

(8.2)

Cостояние системы, описываемой уравнениями (8.2), определяется в каждый момент времени величиной координаты и скоростью её изменения. Это состояние системы можно отобразить точкой на плоскости с координатами , , называемой фазовой плоскостью. При изменении состояния системы изображающая точка перемещается на фазовой плоскости по кривым, которые называют фазовыми траекториями. Cовокупность фазовых траекторий, построенных для различных начальных условий, определяет все возможные процессы в системе и служит наглядным изображением её динамических свойств.

Для получения уравнения фазовых траекторий исключим из (8.2) время, поделив второе уравнение на первое:

(8.3)

Интегрирование нелинейного дифференциального уравнения (8.3) позволяет найти уравнение фазовой траектории:

. (8.4)

8.3 Методы кусочно-линейной аппроксимации и гармонической линеаризации

8.3.1.Метод кусочно-линейной аппроксимации

Используется в том случае, когда нелинейная часть системы безынерционна и её характеристика может быть аппроксимирована прямолинейными участками.

Для каждого участка процессы в системе описываются линейными дифференциальными уравнениями, решение которых может быть найдено. Значения переменных в конце данного участка являются начальными условиями для последующего участка. Таким образом удаётся построить фазовую траекторию движения системы.

8.3.2.Метод гармонической линеаризации

Этот метод базируется на замене нелинейного элемента линейным звеном, параметры которого определяются при синусоидальном входном сигнале из условия равенства амплитуд первых гармоник на выходе нелинейного элемента и эквивалентного ему линейного звена. Данный метод может быть использован в том случае, когда линейная часть системы является низкочастотным фильтром, т.е. отфильтровывает все возникающие на выходе нелинейного звена гармонические составляющие, кроме первой гармоники.

Пусть нелинейное звено является статическим. На вход звена действует сигнал:

На выходе этого звена действует сигнал:

Разложив его в ряд Фурье, получим:

, (8.5)

где - cлагаемое, учитывающее вторые и более высокие гармонические составляющие.

Коэффициенты ряда Фурье имеют вид:

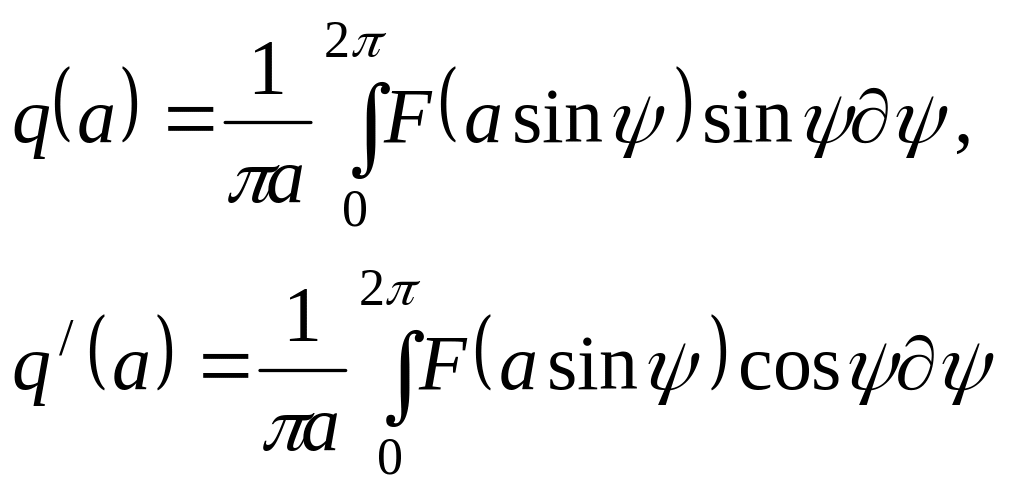(8.6)

Так как , где , то (8.5) можно записать в виде:

. (8.7)

Это выражение называют уравнением гармонической линеаризации, а коэффициенты и - коэффициентами гармонической линеаризации.

Представляется возможным сделать следующий вывод:

При постоянных значениях амплитуды входного сигнала коэффициенты гармонической линеаризации являются постоянными. Различным амплитудам входного сигнала соответствуют различные коэффициенты гармонической линеаризации. В обычной линеаризации коэффициенты не зависят от амплитуды входного сигнала, а определяются только видом характеристики нелинейного звена.

Уравнение гармонической линеаризации (8.7) – это линейное уравнение, поэтому и вся система радиоавтоматики становится линейной. Для её исследования могут быть использованы методы, разработанные для линейных систем. Зависимость коэффициентов гармонической линеаризации от амплитуды сигнала на входе нелинейного звена позволяет выявить специфические свойства нелинейных систем, которые не могут быть определены при использовании обычной линеаризации.