§1.2. Законы распределения непрерывных случайных величин. Нормальное распределение

Функция распределения F(x) определяет вероятность того, что случайная величина X в результате испытания примет значение, меньшее x :

F(x) = P( X < x ).

Случайная величина называется непрерывной, если ее функция распределения F(x) есть непрерывная функция, кусочно-дифференцируемая с непрерывной производной.

Свойства F(x) :

• значения F(x) удовлетворяют двустороннему неравенству 0 ≤ F(x) ≤ 1;

• F(x) – функция неубывающая ;

• P( a ≤ X ≤ b ) = F(b) – F(a) .

Следствие. Вероятность того, что непрерывная случайная величина X примет одно определенное значение, равна 0.

Однако имеет смысл учитывать вероятность попадания значения случайной величины в определенный интервал, каким бы малым он ни был, что и определяется третьим свойством.

Непрерывную случайную величину можно задать с помощью плотности распределения. Плотность распределения вероятностей непрерывной случайной величины X называется функция f(x) = F'(x). Вероятность попадания значения случайной величины в заданный интервал вычисляется так:

P( a ≤ X ≤b ) =

График плотности распределения называется кривой распределения.

Свойства f(x) : f(x) ≥ 0 ; =1. Это означает, что график расположен выше оси Ox, а площадь криволинейной трапеции, ограниченной кривой распределения, равна 1.

Кривой распределения генеральной совокупности непрерывных случайных величин соответствует гистограмма. Гистограмма частот – это ступенчатая фигура, состоящая из прямоугольников, основаниями которых служат частичные интервалы длиной h , а высоты равны отношению n_i/h . Для гистограммы относительных частот высоты прямоугольников равны отношению n_xi/h. Причем площадь гистограммы равна 1, как и площадь, ограниченная теоретической кривой распределения.

Числовые характеристики непрерывных случайных величин, заданных плотностью распределения f(x) , вычисляются так:

математическое ожидание M(x) = ;

дисперсия D(x) = ;

среднее квадратическое отклонение σ(x) = .

При решении практических задач сталкиваются с различными распределениями непрерывной случайной величины. Плотности их распределения называются законами распределения. Часто встречаются законы: равномерной плотности, нормальный, показательный. Особую роль играет нормальный закон.

Нормальным называется распределение вероятностей непрерывной случайной величины, которое описывается плотностью:

Нормальное распределение определяется двумя параметрами: математическим ожиданием a и средним квадратическим отклонением σ . График плотности нормального распределения называется нормальной кривой или кривой Гаусса.

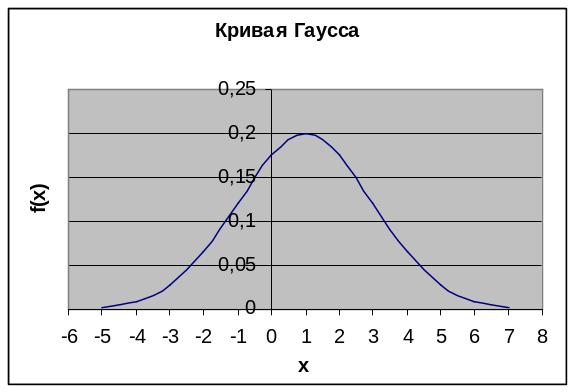
Свойства кривой распределения :

• При x=a функция имеет max = 1/ ;

• Изменение величины параметра a не изменяет формы нормальной кривой, а только приводит к сдвигу вдоль оси Ox;

• С возрастанием σ максимальная ордината уменьшается, а сама кривая становится более пологой, а при убывании σ кривая становится более «остро вершинной»;

• Вероятность попадания нормальной случайной величины в заданный интервал

P(α < X < β) = Φ( ) - Φ ,

где Φ(x) – функция Лапласа ( табулированная функция, которая определяет вероятность попадания случайной величины в интервал (0,x)).

На рисунке приведена кривая распределения случайной величины, имеющей математическое ожидание a = 1 и σ = 2.

Абсолютная величина отклонения нормально распределенной случайной величины от математического ожидания не превосходит утроенного среднего квадратического отклонения. Это свойство называется «правилом 3σ ». Если случайная величина обладает этим свойством, то есть основания предполагать, что она распределена нормально.

Нормально распределенные случайные величины широко распространены на практике. Это объясняется центральной предельной теоремой Ляпунова А.М. : если случайная величина X представляет собой сумму очень большого числа взаимно независимых случайных величин, влияние каждой из которых на всю сумму ничтожно мало, то X имеет распределение, близкое к нормальному. Примером может служить суммарная ошибка измерений или вычислений.

При изучении распределений, отличных от нормального, возникает необходимость количественно оценить это отличие. С этой целью вводят специальные характеристики, в частности асимметрию и эксцесс. Для нормального распределения они равны 0. Небольшие их значения дают возможность предположить, что распределение близко к нормальному.

Асимметрия теоретического распределения A_s = μ₃/σ³, где μ₃ - центральный момент 3-го порядка, σ – среднее квадратическое отклонение.

A_s > 0, если «длинная часть» кривой расположена справа от математического ожидания, и A_s < 0, если – слева.

Эксцесс теоретического распределения E_k = ( μ₄/σ⁴ ) – 3 , где μ₄ – центральный момент 4-го порядка. Для нормально распределенной случайной величины μ₄/σ⁴ = 3 и E_k = 0. Если E_k > 0 , кривая распределения имеет более высокую и острую вершину по сравнению с нормальной кривой, если E_k < 0 – более низкую и плоскую.

Кривая нормального распределения является очень важным понятием в статистике. Она является центральной для теории статистических исследований. В сочетании со стандартным отклонением она может быть использована и для построения точных описательных статистик эмпирического распределения.

Кривая нормального распределения – это теоретическая модель, представляющая собой абсолютно симметричный и гладкий вид полигона частот. Важнейшее свойство кривой нормального распределения – расстояние по абсциссе, измеренное в единицах стандартного отклонения s от среднего арифметического распределения, всегда дает одинаковую площадь под кривой. Эта площадь составляет 68,26% общей площади на отрезке [-s, s ]; 95,44% - на отрезке [-2s,2s ] и 99,72% – на отрезке [-3s,3s ]. В связи с этим имеет смысл рассматривать стандартизированные значения, т.е. выраженные в единицах стандартного отклонения : Z = (x_i – )/s . Стандартизированная теоретическая кривая нормального распределения имеет среднее значение, равное 0, и стандартное отклонение, равное 1. Теоретическая кривая нормального распределения глубоко проанализирована и описана. Области, относящиеся ко всем Z-значениям, представлены в табличной форме ( в таблице нормального распределения).